
(一)定义:到定点F与定直线l的距离相等的点的轨迹是抛物线。
即:到定点F的距离与到定直线l的距离之比是常数e(e=1)。
(三)性质
方程: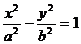
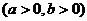
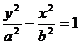
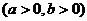
定义域: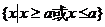 ; 值域为R;
; 值域为R;
实轴长=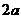 ,虚轴长=2b
,虚轴长=2b
焦距:2c
准线方程: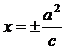
焦半径: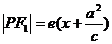 ,
,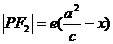 ,
,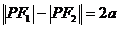 ;
;
注意:(1)图中线段的几何特征: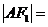
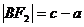 ,
,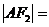
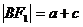
顶点到准线的距离: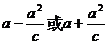 ;焦点到准线的距离:
;焦点到准线的距离: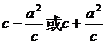
两准线间的距离=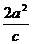
(2)若双曲线方程为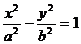
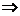 渐近线方程:
渐近线方程: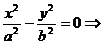
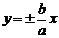
若渐近线方程为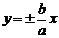
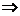
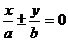
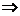 双曲线可设为
双曲线可设为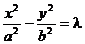
若双曲线与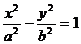 有公共渐近线,可设为
有公共渐近线,可设为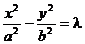
(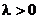 ,焦点在x轴上,
,焦点在x轴上,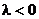 ,焦点在y轴上)
,焦点在y轴上)
(3)特别地当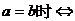 离心率
离心率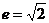
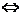 两渐近线互相垂直,分别为y=
两渐近线互相垂直,分别为y=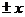 ,此时双曲线为等轴双曲线,可设为
,此时双曲线为等轴双曲线,可设为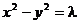 ;
;
(4)注意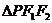 中结合定义
中结合定义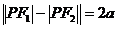 与余弦定理
与余弦定理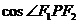 ,将有关线段
,将有关线段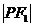 、
、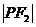 、
、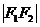 和角结合起来。
和角结合起来。
(5)完成当焦点在y轴上时,标准方程及相应性质。
(二)图形:
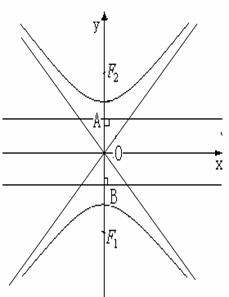
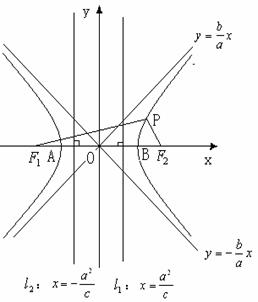
(一)定义:Ⅰ若F1,F2是两定点,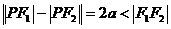 (
(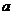 为常数),则动点P的轨迹是双曲线。
为常数),则动点P的轨迹是双曲线。
Ⅱ若动点P到定点F与定直线l的距离之比是常数e(e>1),则动点P的轨迹是双曲线。
(一)椭圆
定义Ⅰ:若F1,F2是两定点,P为动点,且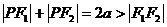 (
(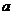 为常数)则P点的轨迹是椭圆。
为常数)则P点的轨迹是椭圆。
定义Ⅱ:若F1为定点,l为定直线,动点P到F1的距离与到定直线l的距离之比为常数e(0<e<1),则P点的轨迹是椭圆。
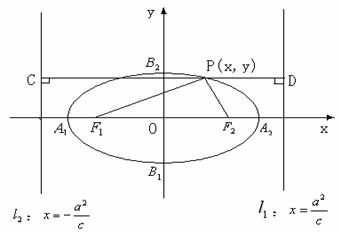 标准方程:
标准方程: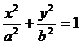
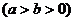
定义域: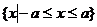 值域:
值域: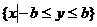
长轴长=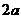 ,短轴长=2b
,短轴长=2b
焦距:2c
准线方程: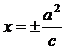
焦半径: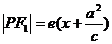 ,
,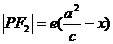 ,
,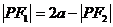 ,
,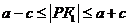 等(注意涉及焦半径①用点P坐标表示,②第一定义。)
等(注意涉及焦半径①用点P坐标表示,②第一定义。)
注意:(1)图中线段的几何特征: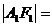
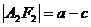 ,
,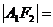
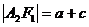
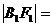
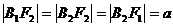 ,
,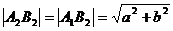 等等。顶点与准线距离、焦点与准线距离分别与
等等。顶点与准线距离、焦点与准线距离分别与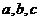 有关。
有关。
(2)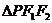 中经常利用余弦定理、三角形面积公式将有关线段
中经常利用余弦定理、三角形面积公式将有关线段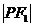 、
、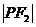 、2c,有关角
、2c,有关角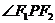 结合起来,建立
结合起来,建立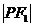 +
+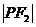 、
、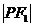
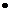
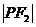 等关系
等关系
(3)椭圆上的点有时常用到三角换元: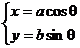 ;
;
(4)注意题目中椭圆的焦点在x轴上还是在y轴上,请补充当焦点在y轴上时,其相应的性质。
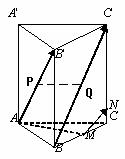
26. 如图:已知正三棱柱ABC-A'B'C'的侧棱长为2,底面边长为1,M是BC的中点。 (1)求异面直线AB'与BC'的夹角; (2)在直线CC'上求一点N,使得MN⊥AB'。
(3) 若AB的中点为P,BC’的中点Q,求证:PQ//面ABC (1)解法一:因为 又因为ABC-A'B'C'是正三棱柱,∴ < 由题意,=2从而得:===4+ = ∴ cos< ∴ < 即异面直线AB'与BC'的夹角为arccos 解法二:以A点为坐标原点,AA'为z轴,AC为y轴,建立空间直角坐标系, 由题意:A(0,0,0),B(,0),B'(,2),C'(0,1,2) cos<= ∴ < 即异面直线AB'与BC'的夹角为arccos (2)解法一:设由题意可得:
< ∵ 也就是 ∴ ∴ ∴ -+4x=0∴ x= 即当时,AB'⊥MN. 解法二:同解法一建立空间直角坐标系, 有A(0,0,0),B(,0),M(,0),N(0,1,z) ∵ ∴ ∴ -+2z=0 解得z=,∴ N=(0,1,) 即CN=时,AB'⊥MN.
(3)非向量法略,另向量法:方法一、基向量(待定系数法)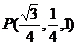
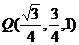 ,则
,则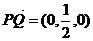 ,又因为
,又因为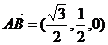 ,
,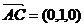
设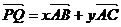 得
得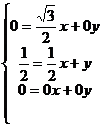 得x=0,y=1/2,所以
得x=0,y=1/2,所以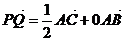 所以PQ与面ABC共面,又因为
所以PQ与面ABC共面,又因为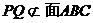 ,所以PQ//面ABC
,所以PQ//面ABC
例2已知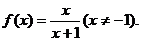 (来源课本第二册P17、EX9;P23、EX4;P31、EX3)
(来源课本第二册P17、EX9;P23、EX4;P31、EX3)
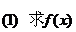 的单调区间;(2)求证:
的单调区间;(2)求证: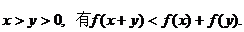
(3)若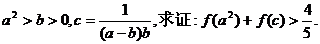
讲解: (1) 对 已 知 函 数 进 行 降 次 分 项 变 形 , 得 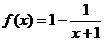 ,
,
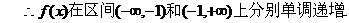
(2)首先证明任意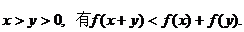 事实上,
事实上,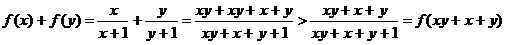
而 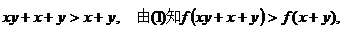
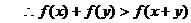
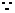
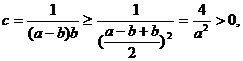
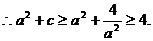
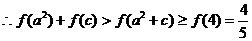 .
.
函 数 与 不 等
式 证 明 的 综 合 题 在 高 考 中 常 考 常 新 , 是 既 考 知 识 又 考 能 力 的 好 题 型 , 在 高 考 备 考 中 有 较 高 的 训 练 价 值.. 针对本例的求解, 你能够想到证明任意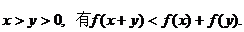 采用逆向分析法,
给出你的想法!
采用逆向分析法,
给出你的想法!
例4 对于函数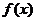 ,若存在
,若存在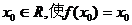 成立,则称
成立,则称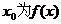 的不动点。如果函数
的不动点。如果函数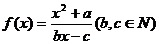 有且只有两个不动点0,2,且
有且只有两个不动点0,2,且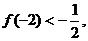
(1)求函数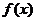 的解析式;
的解析式;
(2)已知各项不为零的数列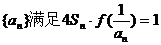 ,求数列通项
,求数列通项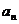 ;
;
(3)如果数列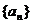 满足
满足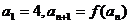 ,求证:当
,求证:当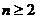 时,恒有
时,恒有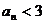 成立.
成立.
讲解: 依题意有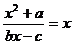 ,化简为
,化简为 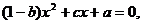 由违达定理, 得
由违达定理, 得
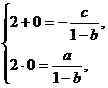 解得
解得 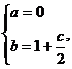 代入表达式
代入表达式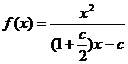 ,由
,由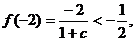 得
得 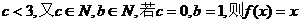 不止有两个不动点,
不止有两个不动点,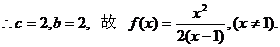
(2)由题设得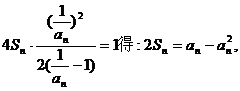 (*)
(*)
且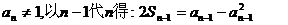 (**)
(**)
由(*)与(**)两式相减得:
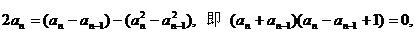
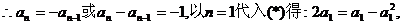
解得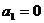 (舍去)或
(舍去)或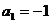 ,由
,由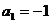 ,若
,若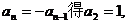 这与
这与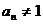 矛盾,
矛盾,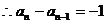 ,即{
,即{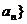 是以-1为首项,-1为公差的等差数列,
是以-1为首项,-1为公差的等差数列,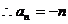 ;
;
(3)采用反证法,假设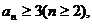 则由(1)知
则由(1)知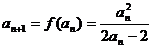
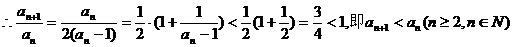 ,有
,有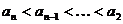 ,而当
,而当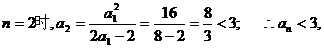 这与假设矛盾,故假设不成立,
这与假设矛盾,故假设不成立,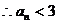 .
.
关于本例的第(3)题,我们还可给出直接证法,事实上:
由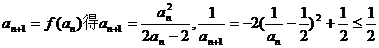 得
得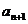 <0或
<0或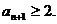
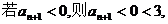 结论成立;
结论成立;
若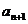
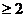 ,此时
,此时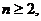 从而
从而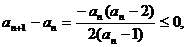 即数列{
即数列{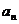 }在
}在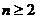 时单调递减,由
时单调递减,由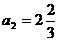 ,可知
,可知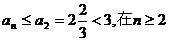 上成立.
上成立.
比较上述两种证法,你能找出其中的异同吗? 数学解题后需要进行必要的反思, 学会反思才能长进.
解析几何中的基本公式
1、 两点间距离:若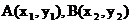 ,则
,则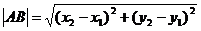
特别地: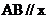 轴, 则
轴, 则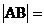 。
。
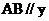 轴, 则
轴, 则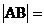 。
。
2、 平行线间距离:若
则: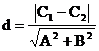
注意点:x,y对应项系数应相等。
3、 点到直线的距离: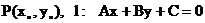
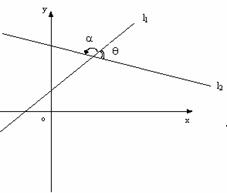 则P到l的距离为:
则P到l的距离为: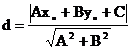
4、 直线与圆锥曲线相交的弦长公式: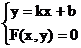
消y: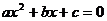 ,务必注意
,务必注意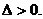
若l与曲线交于A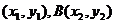
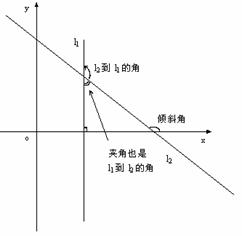 则:
则: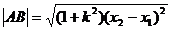
5、 若A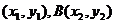 ,P(x,y)。P在直线AB上,且P分有向线段AB所成的比为
,P(x,y)。P在直线AB上,且P分有向线段AB所成的比为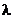 ,
,
则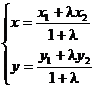 ,特别地:
,特别地: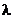 =1时,P为AB中点且
=1时,P为AB中点且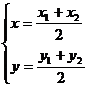
变形后: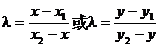
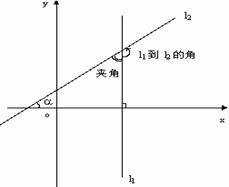
6、 若直线l1的斜率为k1,直线l2的斜率为k2,则l1到l2的角为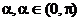
适用范围:k1,k2都存在且k1k2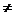 -1 ,
-1 , 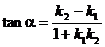
若l1与l2的夹角为 ,则
,则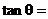
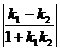 ,
,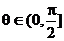
注意:(1)l1到l2的角,指从l1按逆时针方向旋转到l2所成的角,范围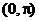
l1到l2的夹角:指 l1、l2相交所成的锐角或直角。
(2)l1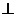 l2时,夹角、到角=
l2时,夹角、到角=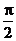 。
。
(3)当l1与l2中有一条不存在斜率时,画图,求到角或夹角。
7、 (1)倾斜角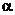 ,
,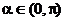 ;
;
(2)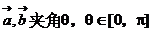 ;
;
(3)直线l与平面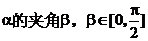 ;
;
(4)l1与l2的夹角为 ,
,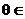
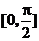 ,其中l1//l2时夹角
,其中l1//l2时夹角 =0;
=0;
(5)二面角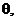
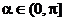 ;
;
(6)l1到l2的角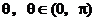
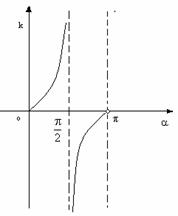
8、 直线的倾斜角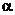 与斜率k的关系
与斜率k的关系
a)
每一条直线都有倾斜角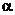 ,但不一定有斜率。
,但不一定有斜率。
b)
若直线存在斜率k,而倾斜角为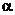 ,则k=tan
,则k=tan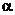 。
。
9、 直线l1与直线l2的的平行与垂直
(1)若l1,l2均存在斜率且不重合:①l1//l2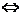 k1=k2
k1=k2
②l1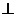 l2
l2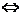 k1k2=-1
k1k2=-1
(2)若
若A1、A2、B1、B2都不为零
①
l1//l2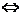
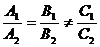 ;
;
②
l1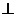 l2
l2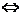 A1A2+B1B2=0;
A1A2+B1B2=0;
③
l1与l2相交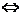
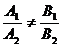
④
l1与l2重合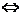
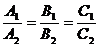 ;
;
注意:若A2或B2中含有字母,应注意讨论字母=0与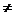 0的情况。
0的情况。
10、 直线方程的五种形式
名称 方程 注意点
斜截式: y=kx+b 应分①斜率不存在
②斜率存在
点斜式:
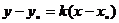 (1)斜率不存在:
(1)斜率不存在: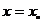
(2)斜率存在时为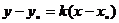
两点式:
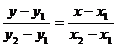
截距式:
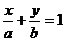 其中l交x轴于
其中l交x轴于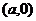 ,交y轴于
,交y轴于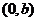 当直线l在坐标轴上,截距相等时应分:
当直线l在坐标轴上,截距相等时应分:
(1)截距=0 设y=kx
(2)截距=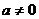 设
设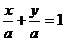
即x+y=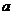
一般式:
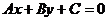 (其中A、B不同时为零)
(其中A、B不同时为零)
10、确定圆需三个独立的条件
圆的方程 (1)标准方程: 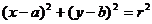 ,
, 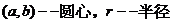 。
。
(2)一般方程: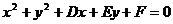 ,(
,(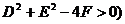
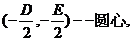
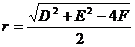
11、直线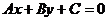 与圆
与圆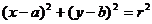 的位置关系有三种
的位置关系有三种
若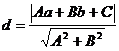 ,
,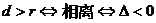
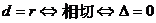
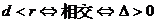
12、两圆位置关系的判定方法
 设两圆圆心分别为O1,O2,半径分别为r1,r2,
设两圆圆心分别为O1,O2,半径分别为r1,r2,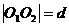
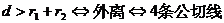
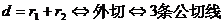
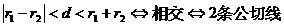
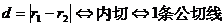
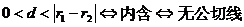
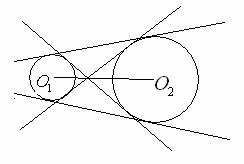
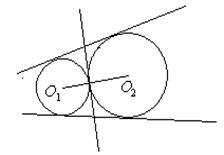
外离 外切
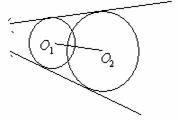
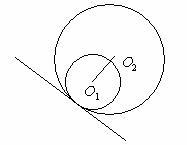
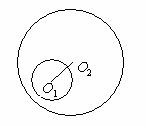
相交 内切 内含
13、圆锥曲线定义、标准方程及性质
25. 在北纬60º圈上有甲、乙两地,它们在纬度线上的弧长等于R,R为地球半径,则这两地的球面距离为( ) A.πR B.πR C.πR D.πR B
填空题:
设m、n是不重合的两条直线,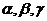 是不重合的平面,给出下列命题:请判断其是否正确,如错误,请举出反例。
是不重合的平面,给出下列命题:请判断其是否正确,如错误,请举出反例。
若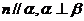 ,则
,则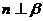
若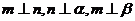 ,则
,则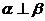
 若
若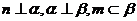 ,则
,则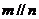
若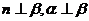 ,则
,则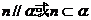
若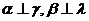 ,则
,则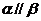
若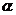 内有不共线的三点到
内有不共线的三点到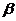 的距离相等,则
的距离相等,则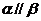
若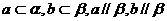 ,则
,则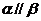
若a、b是异面直线,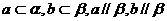 ,则
,则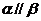
24. 球面上有三个点A、B、C,其中AB=18,BC=24,AC=30,且球心到平面ABC的距离为球半径的一半,那么这个球的半径为( ) A.10 B.10 C.20 D.30 A
23. 球面上有三个点,其中任意两个点的球面距离都等于大圆周长的,经过这三个点的小圆周长为4π,那么这个球的半径为( ) A.4 B.2 C.2 D. B
22. 地球半径为R,在北纬30º的圆上有两点A、B,A点的经度为东经120º,B点的经度为西经60º,则A、B两点的球面距离为( ) A.πR B.πR C.πR D.πR D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com