
5. 定义在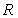 上的偶函数
上的偶函数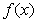 在
在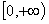 上单调递减,且
上单调递减,且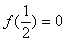 ,则满足
,则满足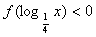 的
的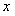 的集合为( )
的集合为( )
A.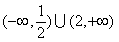 B.
B.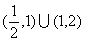 C.
C.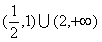 D.
D.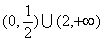
4.已知集合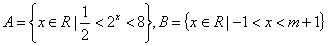 ,若
,若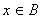 成立的一个充分不必要条件是
成立的一个充分不必要条件是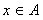 ,则实数
,则实数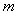 的取值范围是( )
的取值范围是( )
A.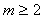 B.
B.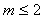 C.
C.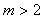 D.
D.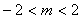
3.将函数y=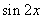 的图像向左平移
的图像向左平移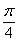 个单位,再向上平移1个单位,所得图像的函数解析式是 (
)
个单位,再向上平移1个单位,所得图像的函数解析式是 (
)
A.y=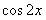 B.y=
B.y=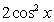 C.y=1+
C.y=1+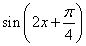 D.y=
D.y=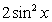
2. 曲线y = 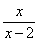 在点(1,-1)处的切线方程为( )
在点(1,-1)处的切线方程为( )
A. y = -2x+1 B. y = -3x+2 C.y = 2x-3 D. y = x-2
1.若集合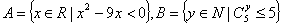 ,则集合
,则集合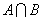 中元素的个数为(
)
中元素的个数为(
)
A.0个 B. 1个 C.2个 D. 3个
21.(本小题满分14分)
解:(I)设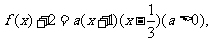 即
即 .………2分
.………2分
 令
令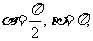 则
则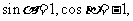 有
有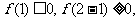 得
得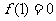 ,即
,即

 得
得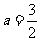 ,
, 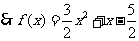 . …………………4分
. …………………4分
(II)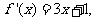 则
则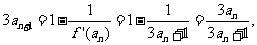 即
即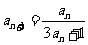 ;…6分
;…6分
两边取倒数,得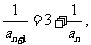 即
即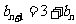 ,
, ∴数列
∴数列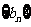 是首项为
是首项为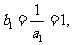 公差为3的等差数列.
………………8分
公差为3的等差数列.
………………8分
 ∴
∴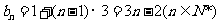 . ………………9分
. ………………9分
(Ⅲ)

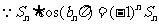 , ∴
, ∴ 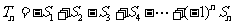 . …………11分
. …………11分
当n为偶数时,

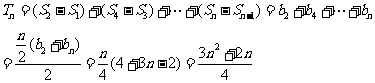 ;…………12分
;…………12分
当n为奇数时,
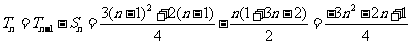 .…………13分
.…………13分
综上,Tn= ……………………14分
……………………14分
20.(本小题满分14分)
解:(Ⅰ)设点T的坐标为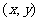 ,点M的坐标为
,点M的坐标为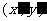 ,则M1的坐标为(0,
,则M1的坐标为(0,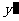 ),
),
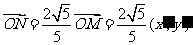 ,于是点N的坐标为
,于是点N的坐标为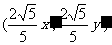 ,N1的坐标
,N1的坐标
为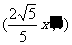 ,所以
,所以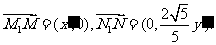 …………2分
…………2分
由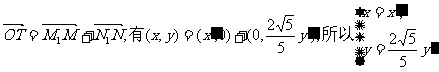
由此得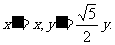 …………4分
…………4分
由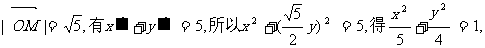
即所求的方程表示的曲线C是椭圆. ……………………6分
(Ⅱ)点A(5,0)在曲线C即椭圆的外部,当直线l的斜率不存在时,直线l与椭圆C
无交点,所以直线l斜率存在,并设为k. 直线l的方程为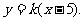 ………8分
………8分
由方程组
依题意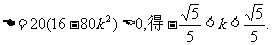 …………10分
…………10分
当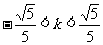 时,设交点
时,设交点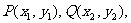 PQ的中点为
PQ的中点为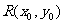 ,
,
则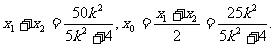
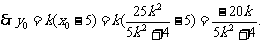
又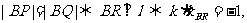 …………12分
…………12分
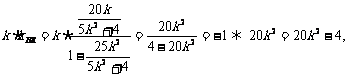
而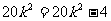 不可能成立,所以不存在直线l,使得|BP|=|BQ|. …………14分
不可能成立,所以不存在直线l,使得|BP|=|BQ|. …………14分
19.(本小题满分14分)
解:(I)由题意得(100-x)·3000·(1+2x%)≥100×3000,
即x2-50x≤0,解得0≤x≤50, ……………………3分
又∵x>0 ∴0<x≤50. ……………………5分
(II)设这100万农民的人均年收入为y元,
则y= =
=-[x-25(a+1)]2+3000+475(a+1)2 (0<x≤50) . ………………8分
(i)当0<25(a+1)≤50,即0<a≤1,当x=25(a+1)时,y最大; ………………10分
(ii)当25(a+1)>50,即a >1,函数y在(0,50]单调递增,∴当x=50时,y取最大值.…………12分
答:在0<a≤1时,安排25(a +1)万人进入企业工作,在a>1时安排50万人进入企业工作,才能使这100万人的人均年收入最大 ………………14分
18.(本小题满分13分)
解:(Ⅰ) (1)该四棱锥相应的俯视图为内含对角线、边长为6cm的正方形如图;……2分
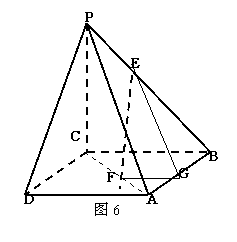
 ……4分
……4分
其面积为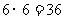 (
(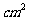 ). ……6分
). ……6分
(Ⅱ)在三角形PAB中,过E作EG//PA,EG交AB于G,连接FG. ……7分
依题意:BE:EP=BG:GA=CF:FA故在三角形BCA中,FG//BC,在正方形ABCD中,AD//BC,所以FG//AD. ……8分
又FG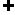 平面
平面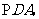 所以,FG//平面PDA,
……10分
所以,FG//平面PDA,
……10分
同理EG//平面PDA. ……11分
由FG与EG相交,得平面EFG//平面PDA,……12分
又EF在平面EFG内,所以EF//平面PDA. ……13分
17.(本小题满分12分)
解:(Ⅰ)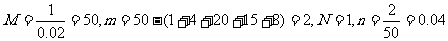 .
.
………………4分
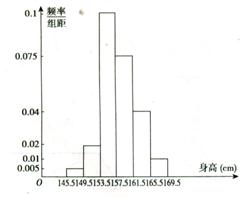 (Ⅱ)作平面直角坐标系,组距为4,纵轴表示频率/组距,横轴表示身高,画出直方图如图.
(Ⅱ)作平面直角坐标系,组距为4,纵轴表示频率/组距,横轴表示身高,画出直方图如图.
………………8分
(Ⅲ)在153.5-157.5范围内最多,估计概率为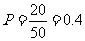 .
………………12分
.
………………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com