
1.山东省兖州市2010届高三上学期模块检测2009年2月11日,美国和俄罗斯的两颗卫星在西伯利亚上空相撞,这是有史以来首次卫星碰撞事件,碰撞点比相对地球静止的国际空间站高434km.则 ( AB )
A.在碰撞点高度运行的卫星的周期比国际空间站的周期大
B.在碰撞点高度运行的卫星的向心加速度比国际空间站的向心加速度小
C.在与空间站相同轨道上运行的卫星一旦加速,将有可能与空间站相撞
D.若发射一颗在碰撞点高度处运行的卫星,发射速度至少为11.2km/s
证一:(分析法)由于不等式两边均为正数,平方后只须证:
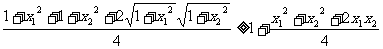
即: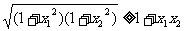
再平方: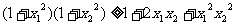
化简整理得: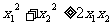 (显然成立)
(显然成立)
∴原式成立
证二:(反证法)假设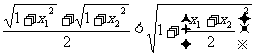
 化简可得:
化简可得: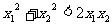 (不可能)
(不可能)
∴原式成立
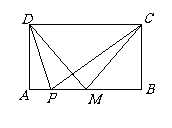
证三:(构造法)构造矩形ABCD,
使AB = CD = 1, BP = x1, PC = x2
当ÐAPB = ÐDPC时,AP + PD为最短。
取BC中点M,有ÐAMB = ÐDMC, BM = MC
=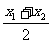
∴ AP + PD ≥ AM + MD
即:
∴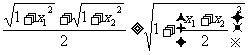
证一:(分析法)∵a, b, c, d, x, y都是正数
∴要证:xy≥ac + bd
只需证:(xy)2≥(ac + bd)2
即:(a2 + b2)(c2 + d2)≥a2c2 + b2d2 + 2abcd
展开得:a2c2 + b2d2 + a2d2 + b2c2≥a2c2 + b2d2 + 2abcd
即:a2d2 + b2c2≥2abcd 由基本不等式,显然成立
∴xy≥ac + bd
证二:(综合法)xy =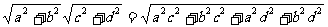
≥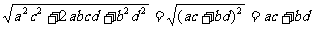
证三:(三角代换法)
∵x2 = a2 + b2,∴不妨设a = xsina, b = xcosa
y2 = c2 + d2 c = ysinb, d = ycosb
∴ac + bd = xysinasinb + xycosacosb = xycos(a - b)≤xy
解一: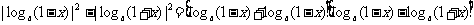
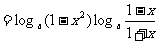
∵0 < 1 - x2 < 1, 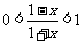 ∴
∴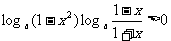
∴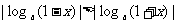
解二: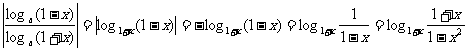
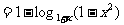
∵0 < 1 - x2 < 1, 1
+ x > 1, ∴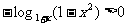
∴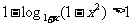 ∴
∴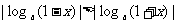
解三:∵0 < x < 1, ∴0 < 1 - x < 1, 1 < 1 + x < 2,
∴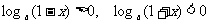
∴左 - 右 = 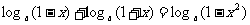
∵0 < 1 - x2 < 1, 且0 < a < 1 ∴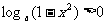
∴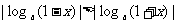
变题:若将a的取值范围改为a > 0且a ¹ 1,其余条件不变。
比较、综合、分析、换元、反证、放缩、构造
20、设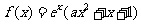 ,且曲线y=f(x)在x=1处的切线与x轴平行。
,且曲线y=f(x)在x=1处的切线与x轴平行。
(1)求a的值,并讨论f(x)的单调性;
(2)证明:当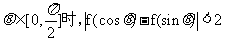 (14分)
(14分)
19、设函数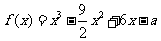 .
.
(1)对于任意实数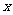 ,
,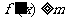 恒成立,求
恒成立,求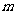 的最大值;
的最大值;
(2)若方程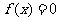 有且仅有一个实根,求
有且仅有一个实根,求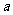 的取值范围. (14分) (14分(
的取值范围. (14分) (14分(
18、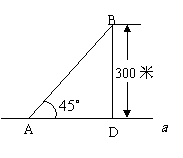 如图,某海滨浴场的岸边可近似地看作直线
如图,某海滨浴场的岸边可近似地看作直线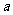 ,救生员现在岸边的A处,发现海中的B处有人求救,救生员没有直接从A处游向B处,而是沿岸边A跑到离B最近的D处,然后游向B处,若救生员在岸边的行进速度为6米/秒,在海水中的行进速度为2米/秒.
,救生员现在岸边的A处,发现海中的B处有人求救,救生员没有直接从A处游向B处,而是沿岸边A跑到离B最近的D处,然后游向B处,若救生员在岸边的行进速度为6米/秒,在海水中的行进速度为2米/秒.
(1)分析救生员的选择是否正确?
(2)在AD上找一处C,使救生员从A到B的时间最短,并求出最短时间。(13分)
17、一次函数f(x)是R上的增函数且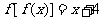 ,二次函数g(x)满足
,二次函数g(x)满足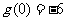 ,
,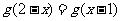 且g(x)的最小值为
且g(x)的最小值为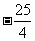 .
.
(1)求f(x),g(x)的解析式;
(2)当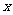 满足
满足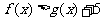 时,求函数
时,求函数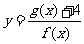 的值域.(14分)
的值域.(14分)
16、在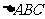 中,
中, 为锐角,角
为锐角,角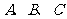 所对的边分别为
所对的边分别为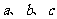 ,且
,且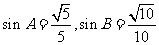
(I)求 的值;
的值;
(II)若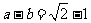 ,求
,求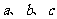 的值。w(13分)
的值。w(13分) 

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com