
4.把下列句子组成语意连贯的一段文字,排序最恰当的一项是(3分)
①“神采”是书家在书作中显示的精神风采。
②我们欣赏书法美,还须超越书法的外在状貌和书写的“笔力”、“笔势”,深入到书法家的内心世界,所谓“玩迹探情”。
③因其生于用笔,只有“深识书者”才能感知。
④古人早就说过,“笔迹者界也,流美者人也”,“书则一字已见其心。”
⑤所以欣赏书法美的最高境界是“惟观神采,不见字形”,犹如庄子所谓“得鱼忘筌”。
A.④⑤①②③ B.②④⑤①③ C.④②⑤①③ D.②④①③⑤
3.下列句子中,没有语病的一项是(3分)
A.湛江政府建造了集生态保护、休闲娱乐、观赏文化于一体的南国花园是我市公园中一座富有热带园林植物景观特色的综合性公园。
B.从群众意见的具体内容看,群众关注的热点十分广泛,其中,关于加强医疗卫生服务体系建设的意见最多。
C.人力资源和社会保障部副部长张小建表示,在当前全球性经济波动对就业产生直接冲击的情况下,高校毕业生就业面临严峻挑战。
D.一度因收益不高而备受冷落的分红型保险产品,在投资理财市场风险加大之时,投资者重新把目光投向相对稳健的理财产品,分红型保险产品重新走俏市场。
2.下列各句中加点的词语,使用恰当的一句是 (3分)
A.戴骁军冒天下之大不韪,曝光了山西霍宝干河煤矿给记者发“封口费”的消息。
B.村民们对司空见惯的珊瑚屋舍不以为然,一些年久失修的无人居住的珊瑚屋舍开始倒塌。
C.2008年奥运开幕式上那鼓声如骤雨,如旋风,气势磅礴,给观众留下了深刻印象。
D.陈凯歌为《梅兰芳》上演作了大量宣传,并在首映式上坐而论道,引起各大传媒的关注。
1.下列词语中加点的字,每对的读音都不相同的一组是(3分)
A.与会/参与 坍塌/殚精竭虑 高亢/引吭高歌
B.塑造/追溯 处所/处之泰然 骨髓/绥靖政策
C.角度/角色 腼腆/暴殄天物 中间 /仲秋之夜
D.纵横/横财 凋零/ 风流倜傥 歼灭/阡陌交通
例4
在数列 中,
中,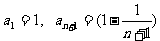 an(n∈N*),
an(n∈N*),
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若对于一切n>1的自然数,不等式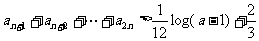 恒成立,试求实数a的取值范围.
恒成立,试求实数a的取值范围.
解:(Ⅰ)因为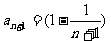 ,an(n∈N*),a=1,所以an>0.
,an(n∈N*),a=1,所以an>0.
所以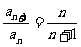 . 所以
. 所以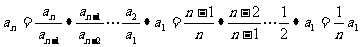 . 而a1=1,所以
. 而a1=1,所以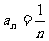 .
.
(Ⅱ)设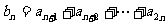 (n∈N*),m
(n∈N*),m
由(Ⅰ)知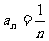 ,所以
,所以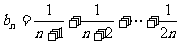 ,所以
,所以
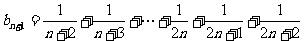 ,所以
,所以
 .
.
所以数列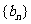 是单调递增数列.
是单调递增数列.
所以当 时,bn的最小值为
时,bn的最小值为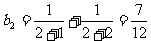 . 所以要使对于一切n>1的自然数,不等式
. 所以要使对于一切n>1的自然数,不等式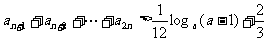 恒成立,则需且只需
恒成立,则需且只需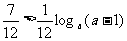
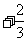 ,则
,则 . 所以
. 所以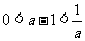 ,解之得
,解之得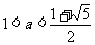 .
.
故所求实数a的取值范围为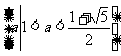 .
.
评注 本题(Ⅱ)中的恒成立问题的解决关键,是灵活化归为求数列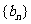 自第2项起的各项中最小项问题.
自第2项起的各项中最小项问题.
体会 求数列中的最大项或最小项,有些题目有多种途径能够解决(如例1),一题多解可以开阔思路;有些题目,不是几种方案都能奏效,要有一个尝试判断的思维过程,要能够迅速调整策略(如例2);有些题目,借助辅助函数的单调性加以解决,但要注意数列的自变量只有取正整数时才有意义(如例3);有些与恒成立有关的参数取值范围问题,可以转化为求数列中的最大项或最小项问题加以处理(如例4). 因为数列本身就是一种特殊函数,所以求数列中的最大项或最小项问题,与函数求最大值或最小值的方法有许多相通之外;但也要注意作为特殊函数数列,它的定义域具有鲜明的个性,是正整数集N*(或它的有限子集{1,2,…,n}),这就使得数列的图象是一群孤立的点,求数列中的最大项或最小项问题时,不要忽视这一点.
例3
在数列 中,
中,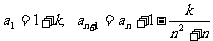 (
(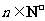 ),其中k是常数,且
),其中k是常数,且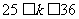 .
.
(Ⅰ)求数列 的通项公式;(Ⅱ)求数列
的通项公式;(Ⅱ)求数列 的最小项.
的最小项.
解 (Ⅰ)因为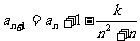 (
(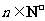 ),所以
),所以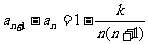 ,即
,即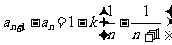 .
.
当 时,
时,
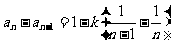 .
.
以上n-1个式子相加得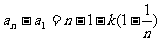 ,即
,即 .
.
又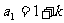 ,所以
,所以 ,即
,即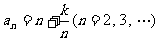 .
.
当n=1时,上式也成立.
所以数列 的通项公式为
的通项公式为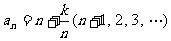 .
.
(Ⅱ)为考查数列 的单调性,注意到
的单调性,注意到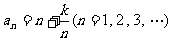 ,可设函数
,可设函数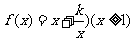 ,则
,则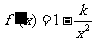 ,即
,即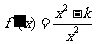 .
.
可知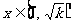 时,
时,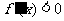 ;
;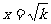 时,
时,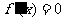 ;
;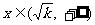 时,
时,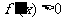 .
.
所以函数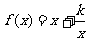 在[1,
在[1,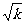 ]上是减函数;在
]上是减函数;在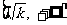 上是增函数.
上是增函数.
因为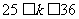 ,所以
,所以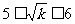 .
.
(1)当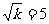 ,即k=25时,
,即k=25时,
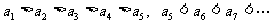 .所以数列
.所以数列 的最小项为
的最小项为
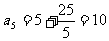 .
.
(2)当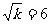 ,即k=36时,
,即k=36时,
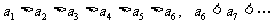 . 所以数列
. 所以数列 的最小项为
的最小项为
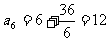 .
.
(3)当a5=a6,即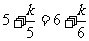 ,即k=30时,
,即k=30时,
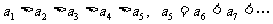 . 所以数列
. 所以数列 的最小项为
的最小项为
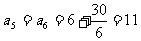 .
.
(4)当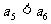 且
且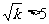 时,
时,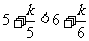 且
且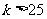 ,则
,则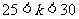 ,
,
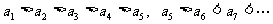 . 所以数列
. 所以数列 的最小项为
的最小项为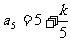 .
.
(5)当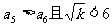 时,
时,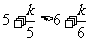 且k<36,则
且k<36,则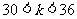 ,
,
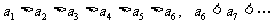 .
.
所以数列 的最小项为
的最小项为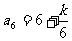 .
.
综上所述:
当k=25时,数列 的最小项为a5=10;当
的最小项为a5=10;当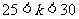 时,数列
时,数列 的最小项为
的最小项为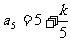 ;当k=30时,数列
;当k=30时,数列 的最小项为a5=a6=11;当30<k<36时,数列
的最小项为a5=a6=11;当30<k<36时,数列 的最小项为
的最小项为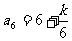 ;当k=36时,数列
;当k=36时,数列 的最小项为a6=12.
的最小项为a6=12.
评注 由(Ⅰ)可知,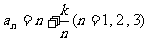 ,则(Ⅱ)中求数列
,则(Ⅱ)中求数列 的最小项问题,易由均值不等式,得
的最小项问题,易由均值不等式,得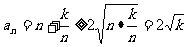 ,从而误认为
,从而误认为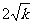 就是最小的项. 实际上这个符号是在
就是最小的项. 实际上这个符号是在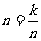 ,即
,即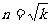 时才能取得. 但根据问题的实际背景,还应要求此时
时才能取得. 但根据问题的实际背景,还应要求此时
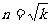 ∈N*,而由条件
∈N*,而由条件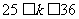 是不能推出一定有
是不能推出一定有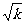 ∈N*的. 解决此问题可以转化为“对勾”函数
∈N*的. 解决此问题可以转化为“对勾”函数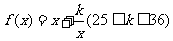 在
在 上的单调性问题. 易求得当
上的单调性问题. 易求得当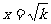 时,函数
时,函数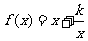 能取得最小值. 但当
能取得最小值. 但当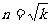 时,
时,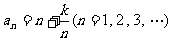 未必能取得最小值. 应根据
未必能取得最小值. 应根据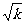 是否为自然数,并结合单调性进行分类讨论. 这也是本题难点所在.
是否为自然数,并结合单调性进行分类讨论. 这也是本题难点所在.
例2
在数列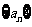 中,
中,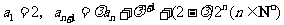 ,其中
,其中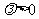 .
.
(Ⅰ)求数列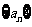 的通项公式;
的通项公式;
(Ⅱ)求数列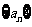 的前
的前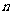 项和
项和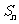 ;
;
(Ⅲ)证明存在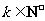 ,使得
,使得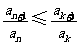 对任意
对任意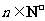 均成立.
均成立.
解 (Ⅰ)由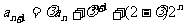 (
(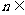 N*),
N*), ,可得
,可得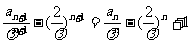 ,所以
,所以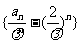 为等差数列,其公差为1,首项为0,故
为等差数列,其公差为1,首项为0,故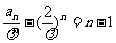 , 所以数列
, 所以数列 的通项公式为
的通项公式为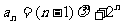 .
.
(Ⅱ)解:设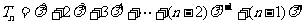 , ①
, ①
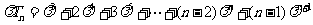 ②
②
当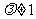 时,①式减去②式,
时,①式减去②式,
得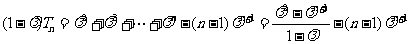 ,
,
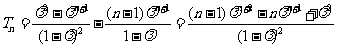 .
.
这时数列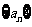 的前
的前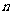 项和
项和 .
.
当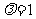 时,
时,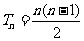 .这时数列
.这时数列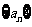 的前
的前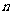 项和
项和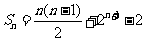 .
.
(Ⅲ)证明:通过分析,推测数列 的第一项
的第一项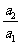 最大,下面证明:
最大,下面证明:
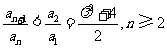 . ③
. ③
由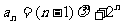 ,
,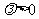 知
知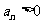 ,要使③式成立,只要
,要使③式成立,只要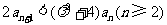 ,
,
因为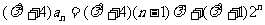
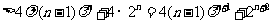
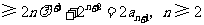 .
.
所以③式成立.
因此,存在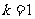 ,使得
,使得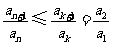 对任意
对任意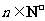 均成立.
均成立.
评注 本题(Ⅲ)设计非常精彩. 为证明“存在k∈N*,使得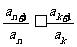 对任意
对任意
n∈N*均成立”,可以转化为思考
“存在k∈N*,使得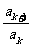 是数列
是数列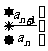 的最大项”问题. 本小题若用差值比较法转化为探究
的最大项”问题. 本小题若用差值比较法转化为探究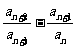 差值与0的大小、用商值比较法转化为探究
差值与0的大小、用商值比较法转化为探究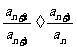 商值与1的大小、用单调性法把通项公式为
商值与1的大小、用单调性法把通项公式为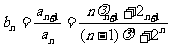 的数列
的数列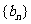 的单调性问题转化为探究函数
的单调性问题转化为探究函数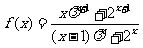 的导数问题以及放缩法解决问题,都颇有难度. 虽然说上述方法都是解决数列最值问题的通性通法,碰壁后若不能及时调整解题策略,就会泥牛入海,不能自拨. 而使用策略五,先敏锐、大胆、果断猜出
的导数问题以及放缩法解决问题,都颇有难度. 虽然说上述方法都是解决数列最值问题的通性通法,碰壁后若不能及时调整解题策略,就会泥牛入海,不能自拨. 而使用策略五,先敏锐、大胆、果断猜出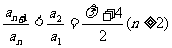 ,再用分析法以及重要不等式证出这个结论,方法非常奏效. 命题高明之处就在于不是直接抛出了
,再用分析法以及重要不等式证出这个结论,方法非常奏效. 命题高明之处就在于不是直接抛出了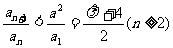 这个结论,让考生去证明;而是让考生先自己探究出结论再论证,富有挑战性. 这也是现在高考命题的一大亮点,要求学生学会先猜后证,能够很好地考查学生思维的深刻性.
这个结论,让考生去证明;而是让考生先自己探究出结论再论证,富有挑战性. 这也是现在高考命题的一大亮点,要求学生学会先猜后证,能够很好地考查学生思维的深刻性.
例1
已知函数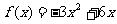 ,Sn是数列
,Sn是数列 的前n项和,点(n,Sn)(n∈N*)在曲线
的前n项和,点(n,Sn)(n∈N*)在曲线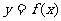 上.
上.
(Ⅰ)求数列 的通项公式;(Ⅱ)若
的通项公式;(Ⅱ)若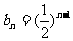 ,
,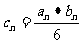 ,且Tn是数列
,且Tn是数列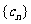 的前n项和. 试问Tn是否存在最大值?若存在,请求出Tn的最大值;若不存在,请说明理由.
的前n项和. 试问Tn是否存在最大值?若存在,请求出Tn的最大值;若不存在,请说明理由.
解(Ⅰ)因为点(n,Sn)在曲线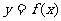 上,又
上,又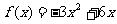 ,所以
,所以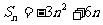 .
.
当n=1时,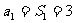 .
.
当n>1时,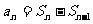
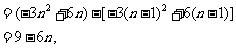
所以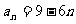 .
.
(Ⅱ)因为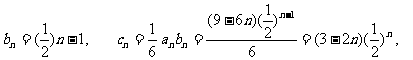 ①所以
①所以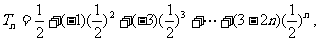 ②
②
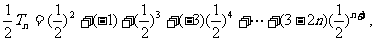 ③
③
②-③得 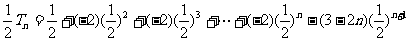
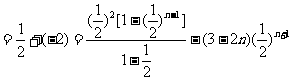 .
.
整理得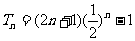 ,
④
,
④
策略一 利用差值比较法
由④式得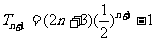 ,所以
,所以
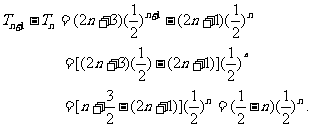
因为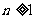 ,所以
,所以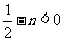 .
.
又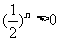 ,所以
,所以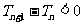 所以
所以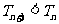 ,
,
所以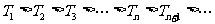 . 所以Tn存在最大值
. 所以Tn存在最大值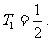
策略二 利用商值比较法
由④式得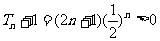 .
.
因为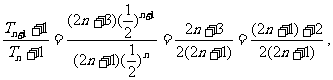
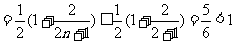
所以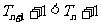 ,即
,即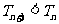 . 所以
. 所以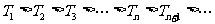 /
/
所以Tn存在最大值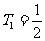 .
.
策略三 利用放缩法
由①式得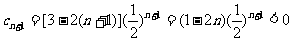 ,又因为Tn是数列
,又因为Tn是数列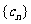 的前n项和,
的前n项和,
所以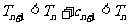 . 所以
. 所以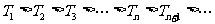
所以Tn存在最大值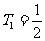 .
.
策略四 利用导数江
考查函数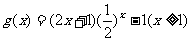 的单调性.
的单调性.
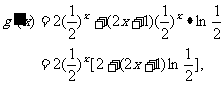
因为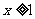 ,所以
,所以 ,而
,而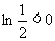 ,所以
,所以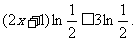
又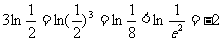 ,
,
所以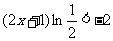 ,所以
,所以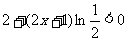 .
.
又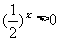 ,所以
,所以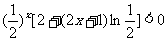 ,
,
即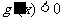 ,所以
,所以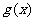 在
在 上是单调递减函数,所以当x=1时,
上是单调递减函数,所以当x=1时,
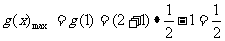 .
.
因为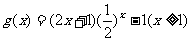 ,所以
,所以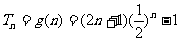 ,
,
所以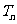 存在最大值
存在最大值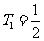 .
.
策略五 先猜后证
通过分析,推测数列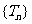 的第一项
的第一项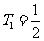 最在.
最在.
下面证明: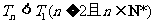 .
.
方法1 分析法
因为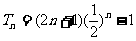 ,所以只要证明
,所以只要证明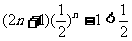 .
.
即只要证明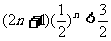 . 只需要证明
. 只需要证明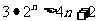 .
.
即只要证明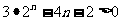
由二项式定理得 且
且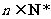 时,
时,
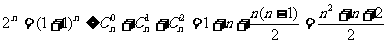 ,所以
,所以
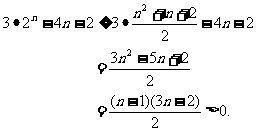
所以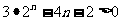 成立. 所以
成立. 所以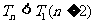 成立.
成立.
所以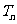 存在最大值
存在最大值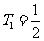 .
.
方法2 利用数学归纳法
(i)当n=2时,因为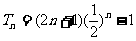 ,所以
,所以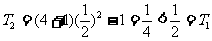 ,不等式成立.
,不等式成立.
(ii)假设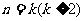 时不等式成立,即
时不等式成立,即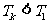 .
.
则当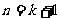 时,
时,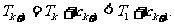
由①式得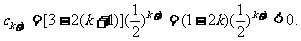 所以
所以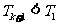 .
.
这就是说,当n=k+1时,不等式也成立.
由(i)(ii)得,对于一切 且
且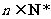 ,总有
,总有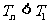 成立.
成立.
所以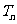 存在最大值
存在最大值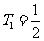 .
.
评注 本题(Ⅱ)的解答给出了求Tn最大值的多种方法,灵活多变,也是求数列最值问题的常规方法.
21.⑴解:函数的定义域为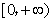 ,
,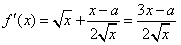 (
(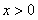 )
)
若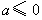 ,则
,则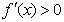 ,
,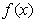 有单调递增区间
有单调递增区间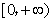 .
.
若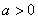 ,令
,令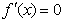 ,得
,得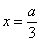 ,
,
当 时,
时,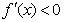 ,
,
当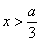 时,
时,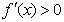 . ……………… (5分)
. ……………… (5分)
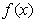 有单调递减区间
有单调递减区间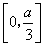 ,单调递增区间
,单调递增区间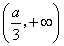 . ……………… (4分)
. ……………… (4分)
⑵解:(i)若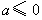 ,
,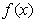 在
在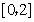 上单调递增,所以
上单调递增,所以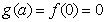 .
.
若 ,
,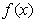 在
在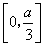 上单调递减,在
上单调递减,在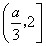 上单调递增,
上单调递增,
所以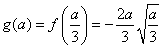 .
.
若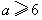 ,
,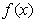 在
在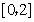 上单调递减,所以
上单调递减,所以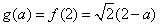 .
.
综上所述,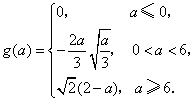 ……………… (9分)
……………… (9分)
(ii)令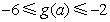 .若
.若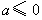 ,无解.
,无解.
若 ,解得
,解得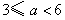 .
.
若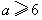 ,解得
,解得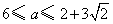 .
.
故的取值范围为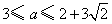 . ………………
(13分)
. ………………
(13分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com