
8.[解析]D.易证 为奇函数,当
为奇函数,当 时,
时, 且
且 单调递增,所以,由奇函数的对称性可知函数的值域为
单调递增,所以,由奇函数的对称性可知函数的值域为 ,因为函数严格单调,所以当
,因为函数严格单调,所以当 有
有 ;计算得
;计算得 ,
, 由数学归纳法可证
由数学归纳法可证 ,所以三个结论都成立,故选D.
,所以三个结论都成立,故选D.
7. [解析]B. 设
[解析]B. 设 ,则满足条件
,则满足条件 的点P在直角坐标平面上对应的区域如图所示,设
的点P在直角坐标平面上对应的区域如图所示,设 ,则
,则 ,由图可知直线在上下两顶点处取得最值,因为区域不包括边界,所以选B.
,由图可知直线在上下两顶点处取得最值,因为区域不包括边界,所以选B.
6.[解析]B.? ,
, ,
,
 .
.
5.[解析]C. 所以
所以 ,整理得:
,整理得: ,故选C.
,故选C.
4.[解析]D.由左视图得2为正三棱柱的高,而 为底面三角形的高,所以底面三角形的边长为4,故选D.
为底面三角形的高,所以底面三角形的边长为4,故选D.
3.[解析]A.跟踪变量得 ,故选A.
,故选A.
2.[解析]A. 
 ,故选A.
,故选A.
1.[解析]C.若 则
则 ,
, ,“
,“ ”是“
”是“ ”的充分条件;若
”的充分条件;若 ,则
,则 ,所以“
,所以“ ”不是“
”不是“ ”的必要条件;选C.
”的必要条件;选C.
21. (本小题满分14分)
已知点 ,点
,点 为
为 ,向量
,向量 ,令
,令 ,
, .
.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)若 在
在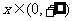 时恒成立,求整数
时恒成立,求整数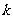 的最大值.
的最大值.
[答案及详细解析]
20. (本小题满分14分)
已知椭圆 的中心在原点
的中心在原点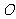 ,焦点在
,焦点在 轴上,直线
轴上,直线 与
与 交于
交于 两点,
两点,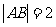 ,且
,且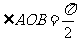 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)若 是椭圆
是椭圆 上两点,满足
上两点,满足 ,求
,求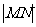 的最小值.
的最小值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com