
1.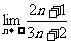
解:原式=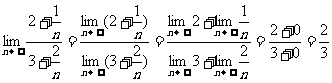
3.语言表达(见教材,略)
此法则可以推广到有限多个数列的情形
解释:如数列  它的极限为1
它的极限为1
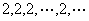 它的极限为2
它的极限为2
则 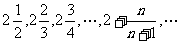 它的极限为3
它的极限为3
即: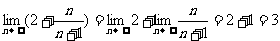
 1.几个需要记忆的常用数列的极限
1.几个需要记忆的常用数列的极限
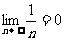
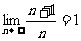
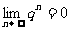
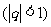
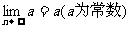
2.运算法则:
 如果
如果 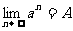
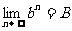
则: 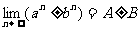
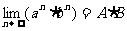
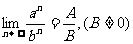
3.某城市的电话号码由六个数字组成,每个数字可以是从0到9这十个数字中的任一个,计算电话号码由六个不同数字组成的概率是多少?
2.一个均匀材料做的正方体玩具,各个面上分别标以数1、2、3、4、5、6。
(1)将这玩具抛掷1次,朝上的一面出现偶数的概率是多少?
(2)将这玩具抛掷2次,朝上的一面的数之和为7的概率是多少?
(3)将这玩具抛掷3次,朝上的一面的数之和为10的概率是多少?
1.把100张已编号的卡片(从1号到100号),从中任取1张,计算:
(1)卡片号是偶数的概率;
(2)卡片号是5的倍数的概率;
(3)卡片号是质数的概率;
(4)卡片号是111的概率;
(5)卡片号是1的概率;
(6)卡片号是从1号到100号中任意一号的数的概率。
用这节中的观点求随机事件的概率时,首先对于在试验中出现的结果的可能性认为是相等的;其次是通过一个比值的计算来确定随机事件的概率,并不需要通过大量重复的试验。因此,从方法上来说这一节所提到的方法,要比上一节所提到的方法简便得多,并且更具有实用价值。
2.等可能性事件概率的计算方法(概率的古典定义):如果一次试验中共有n种等可能出现的结果,其中事件A包含的结果有m种,那么事件A的概率P(A)是m/n(m≤n)。
在上例中:P(A)=52/52=1,
P(B)=13/52=1/4,
P(C)=4/52=1/13。
这里再介绍一种概率古典定义的叙述方法:若事件A1,A2,A3,…,An发生的机会是相同的,则称它们为等可能性事件,其中Ai(i=1,2,…,n)称为基本事件(n为基本事件总数),如果事件A中包含的结果有其中的m种,那么事件A的概率P(A)=m/n,即

1.等可能事件的意义:对于有些随机试验来说,每次试验只可能出现有限个不同的试验结果,而出现所有这些不同结果的可能性是相等的(或叫机会均等原理)。
例如,从52张扑克牌中任意抽取一张(记作事件A),那么不论抽到哪一张都是机会均等的,也就是等可能性的,不论抽到哪一张花色的红心的牌(记作事件B)也都是等可能性的;又不论抽到哪一张印有“A”字样的牌(记作事件C)也都是等可能性的。下面我们给出事件A、B、C发生的概率的概念和计算方法。
随机事件的概率,一般可能通过大量重复试验求得其近似值。但对于某些随机事件,也可能不通过重复试验,而只通过对一次试验中可能出现的结果的分析来计算其概率。这种计算随机事件概率的方法,比经过大量试验得出来的概率,有更简便的运算过程;有更现实的计算方法。
这一节课程的学习,对有关的排列、组合的基本知识和基本思考问题的方法有较高的要求,因此对于排列、组合还不十分熟悉的同学应当先补上这一课。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com