
8.已知x , y∈R+
且x+y=1 , 求证: 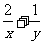 ≥3+2
≥3+2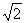
本节学习疑点:
|
学生质疑 |
|
|
教师释疑 |
|
7.求证: log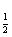 (
(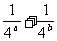 )≤a+b-1
)≤a+b-1
6.已知a , b , c∈R+, 且a+b+c=1, 求证: 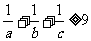
拓展延伸
5.求证: (1) x2+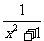
 1
1
(2) 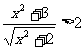
4.设a , b∈(0 , +∞), 求证: 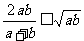
3.求证: (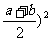 ≤
≤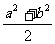
2.若b>a>0 , 则下列不等式一定成立的是 ( )
A. a>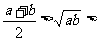 b
b
B. b>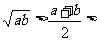 a
a
C. b>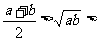 a
a
D.
b>a>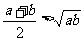
考试热点
1.若a>b>1
, P= , Q =
, Q =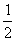 (lga+lgb), R=lg
(lga+lgb), R=lg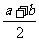 , 则
( )
, 则
( )
A. R<P<Q B. P<Q<R
C. Q<P<R D. P<R<Q
3.已知函数
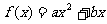 ,若
,若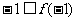
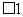 ,
,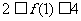 ,求
,求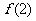 的取值范围.
的取值范围.
答案: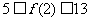 .
. 
1. 某工厂生产甲、乙两种产品,已知生产甲种产品1t,需矿石4t,煤3t,生产乙种产品1t,需矿石5t,煤10t,每1t甲种产品的利润是7万元,每1t乙种产品的利润是12万元,工厂在生产这两种产品的计划中,要求消耗矿石不超过200t,煤不超过300t,则甲、乙两种产品应各生产多少,能使利润总额达到最大?
略解:设甲、乙两种产品分别生产xt,yt,
则约束条件为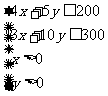 ,
,
利润目标函数为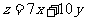 ,利用现性规划知识求解,可得当
,利用现性规划知识求解,可得当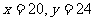 时,
时, 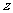 取得最大值.答略.
取得最大值.答略.
|

|

|
A规格 |
B规格 |
C规格 |
||
|
第一种钢板 |
2 |
1 |
1 |
||
|
第二种钢板 |
1 |
2 |
3 |
今需A、B、C三种规格的成品分别为15 , 18 , 27块, 问各截这两种钢板多少张可得所需三种规格成品, 且使所用钢板张数最少?
略解:设需要第一种钢板x张, 需要第二种钢板y张L,钢板总数z张
则约束条件为:
 .
.
目标函数为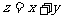 ,利用现性规划知识求解,可得当
,利用现性规划知识求解,可得当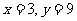 或
或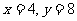 时,
时, 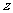 取得最小值12.答略.
取得最小值12.答略.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com