1．直接法(观察法)：

　　 提出课题：函数的值域

1．当x≤1时，由C1、C2的方程中消去y，得x2-(2a+1)x+a2=0，

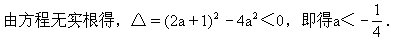
离为d，则

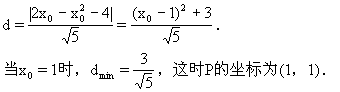
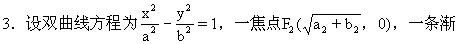
似证明．

3．证明：从双曲线的一个焦点到一条渐近线的距离等于虚半轴长．

作业答案：

2．求抛线y=x2上到直线y=2x-4的距离为最小的点P的坐标．

1．一条定抛物线C1∶y2=1-x与动圆C2∶(x-a)²+y2=1没有公共点，求a的范围．

(三)巩固练习(用一小黑板事先写出．)

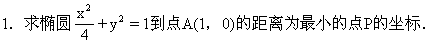
2．已知圆(x-1)²+y2=1与抛物线y2=2px有三个公共点，求P的取值范围．

顶点．

请三个学生演板，其他同学作课堂练习，教师巡视．解答为：

1．设P的坐标为(x，y)，则

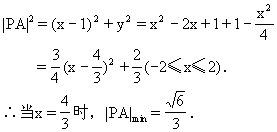
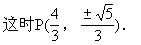
2．由两曲线方程消去y得：x2-(2-2P)x=0．

解得：x1=0，x2=2-2P．

∵0＜x＜2，　 ∴0＜2-2P＜2，　 即0＜P＜1．

故P的取值范围为(0，1)．

四个交点为A(4，1)，B(4，-1)，C(-4，-1)，D(-4，1)．

所以A、B、C、D是矩形的四个顶点．

(二)与圆锥曲线有关的几种典型题

1．圆锥曲线的弦长求法

设圆锥曲线C∶f(x，y)=0与直线l∶y=kx+b相交于A(x1，y1)、B(x₂，y2)两点，则弦长|AB|为：

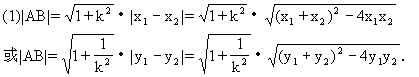
(2)若弦AB过圆锥曲线的焦点F，则可用焦半径求弦长，|AB|=|AF|+|BF|．

A、B两点，旦|AB|=8，求倾斜角α．

分析一：由弦长公式易解．

由学生演板完成．解答为：

∵　 抛物线方程为x2=-4y，　 ∴焦点为(0，-1)．

设直线l的方程为y-(-1)=k(x-0)，即y=kx-1．

将此式代入x2=-4y中得：x2+4kx-4=0．

∴x1+x₂=-4，x1+x2=-4k．

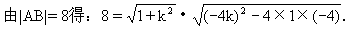
∴ k=±1．

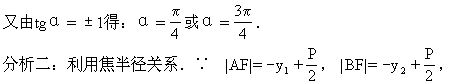
∴|AB|=-(y1+y₂)+p=-[(kx₁-1)+(kx₂-1)]+p=-k(x1+x₂)+2+p．由上述解法易求得结果，由学生课外完成．

2．与圆锥曲线有关的最值(极值)的问题

在解析几何中求最值，关键是建立所求量关于自变量的函数关系，再利用代数方法求出相应的最值．注意点是要考虑曲线上点坐标(x，y)的取值范围．

例2　 已知x2+4(y-1)²=4，求：

(1)x2+y²的最大值与最小值；

(2)x+y的最大值与最小值．

解(1)：

将x2+4(y-1)2=4代入得：

x2+y²=4-4(y-1)2+y²=-3y²+8y

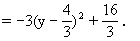
由点(x，y)满足x2+4(y-1)2=4知：

4(y-1)²≤4　 即|y-1|≤1．　 ∴0≤y≤2．

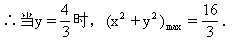
当y=0时，(x2+y²)min=0．

解(2)：

分析：显然采用(1)中方法行不通．如果令u=x+y，则将此代入x2+4(y-1)²=4中得关于y的一元二次方程，借助于判别式可求得最值．

令x+y=u，　 则有x=u-y．

代入x2+4(y-1)2=4得：

5y2-(2u+8)y+u2=0．

又∵0≤y≤2，(由(1)可知)

∴[-(2u+8)]2-4×5×u2≥0．

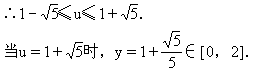
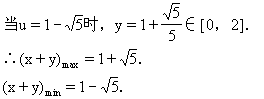
3．与圆锥曲线有关的证明问题

它涉及到线段相等、角相等、直线平行、垂直的证明方法，以及定点、定值问题的判断方法．

例3　 在抛物线x2＝4y上有两点A(x₁，y1)和B(x2，y2)且满足|AB|=y₁+y2+2，求证：

(1)A、B和这抛物线的焦点三点共线；

证明：

(1)∵抛物线的焦点为F(0，1)，准线方程为y=-1．

∴ A、B到准线的距离分别d1＝y1+1，d2=y₂+1(如图2－46所示)．

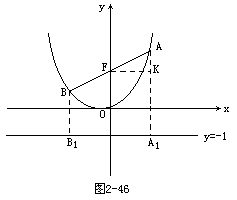
由抛物线的定义：

|AF|=d1=y₁+1，|BF|=d2=y₂+1．

∴|AF|+|BF|=y1+y₂+2=|AB|．

即A、B、F三点共线．

(2)如图2－46，设∠AFK=θ．

∵|AF|=|AA1|=|AK|+2

=|AF|sinθ+2，

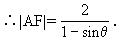
又|BF|=|BB1|=2-|BF|sinθ．

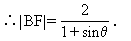
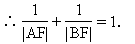
小结：与圆锥曲线有关的证明问题解决的关键是要灵活运用圆锥曲线的定义和几何性质．

4．圆锥曲线与圆锥曲线的相交问题

直线与圆锥曲线相交问题，一般可用两个方程联立后，用△≥0来处理．但用△≥0来判断双圆锥曲线相交问题是不可靠的．解决这类问题：方法1，由“△≥0”与直观图形相结合；方法2，由“△≥0”与根与系数关系相结合；方法3，转换参数法(以后再讲)．

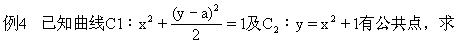
实数a的取值范围．

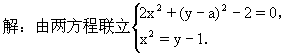
可得：y2=2(1-a)y+a2-4=0．

∵ △=4(1-a)²-4(a²-4)≥0，

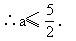
如图2－47，可知：

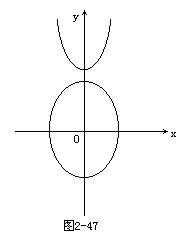
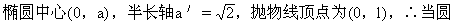
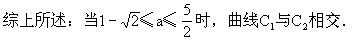
(一)引入

与圆锥曲线有关的几种典型题，如圆锥曲线的弦长求法、与圆锥曲线有关的最值(极值)问题、与圆锥曲线有关的证明问题以及圆锥曲线与圆锥曲线有关的证明问题等，在圆锥曲线的综合应用中经常见到，为了让大家对这方面的知识有一个比较系统的了解，今天来讲一下“与圆锥曲线有关的几种典型题”．

演板、讲解、练习、分析、提问．