
1.平移变换 研究函数y=f(x)与y=f(x+a)+b的图象之间的关系
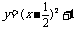 例四、函数
例四、函数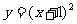 -2和
-2和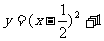 的图象分别是由
的图象分别是由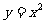 函数的图象经过如何变化得到的。
函数的图象经过如何变化得到的。
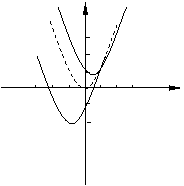
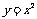 解:
1)将
解:
1)将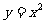 的图象沿 x轴向左平移1个单位再沿y轴向下平移2个单位得
的图象沿 x轴向左平移1个单位再沿y轴向下平移2个单位得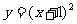 -2的图象;
-2的图象;
|
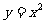 的图象沿x轴向右平移
的图象沿x轴向右平移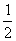 个 单位再沿y轴向上平移1个单位得函数
个 单位再沿y轴向上平移1个单位得函数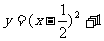 的图象。
的图象。
小结:1。 将函数y=f(x)的图象向左(或向右)平移|k|个单位(k>0向左,k<0向右)得y=f(x+k)图象;
 例三、已知
例三、已知
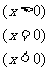
 画出它的图象,并求f(1),f(-2)。
画出它的图象,并求f(1),f(-2)。
解:f(1)=3×12-2=1
f(-2)=-1
 1。
1。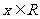 2。
2。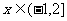 3。
3。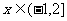 且xÎZ
且xÎZ
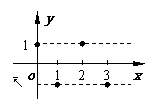 1。
1。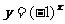
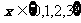 2。
2。 
解:
解: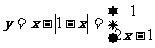
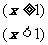
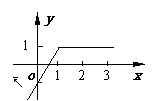
注意:由于定义域从而导致
函数图象只是若干个孤立点。

|
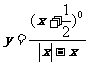 注意:先写成分段函数再作图。
注意:先写成分段函数再作图。
解:定义域为

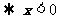 且x¹
且x¹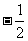
强调:定义域十分重要。
今天主要研究函数的图象。
1.由弦长公式易求得:k=-4
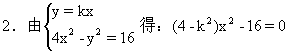
当4-k2=0,k=±2, y=±2x为双曲线的渐近线,直线与双曲线相离
当4-k2≠0时,△=4(4-k2)×(-6)
(1)当△>0,即-2<k<2时,直线与双曲线有两个交点
(2)当△<0,即k<-2或k>2时,直线与双曲线无交点
(3)当△=0,即k=±2时,为渐近线,与双曲线不相切
故当-2<k<2时,直线与双曲线相交
当k≤-2或k≥2时,直线与双曲线相离

3.已知抛物线x=y2+2y上存在关于直线y=x+m对称的相异两点,求m的取值范围.
作业答案:
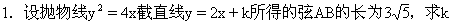
的值.
2.k取何值时,直线y=kx与双曲线4x2-y2=16相交、相切、相离?
(三)小结
本课主要研究了点、直线与圆锥曲线的三种位置关系及重要条件.
(二)讲授新课
1.点M(x0,y0)与圆锥曲线C:f(x,y)=0的位置关系

的焦点为F1、F2,y2=2px(p>0)的焦点为F,一定点为P(x0,y0),M点到抛物线的准线的距离为d,则有:
(由教师引导学生完成,填好小黑板)
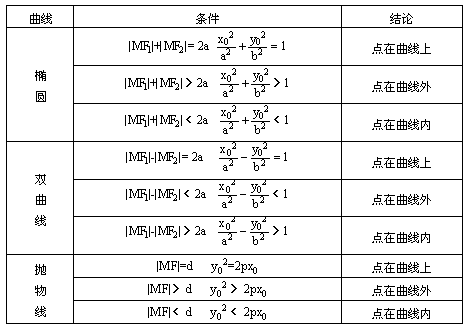
上述结论可以利用定比分点公式,建立两点间的关系进行证明.
2.直线l∶Ax+Bx+C=0与圆锥曲线C∶f(x,y)=0的位置关系:
直线与圆锥曲线的位置关系可分为:相交、相切、相离.对于抛物线来说,平行于对称轴的直线与抛物线相交于一点,但并不是相切;对于双曲线来说,平行于渐近线的直线与双曲线只有一个交点,但并不相切.这三种位置关系的判定条件可引导学生归纳为:
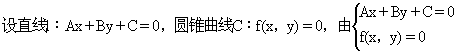
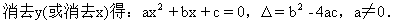
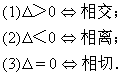
注意:直线与抛物线、双曲线有一个公共点是直线与抛物线、双曲线相切的必要条件,但不是充分条件.
3.应用
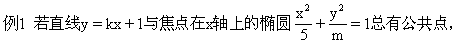
求m的取值范围.
解法一:考虑到直线与椭圆总有公共点,由直线与圆锥曲线的位置关系的充要条件可求.
由一名同学演板.解答为:
由椭圆方程及椭圆的焦点在x轴上,知:0<m<5.
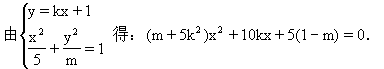
又 ∵直线与椭圆总有公共点,
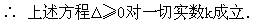
即(10k)2-4x(m+5k2)×5(1-m)≥0,
亦即5k2≥1-m对一切实数k成立.
∴1-m≤0,即m≥1.
故m的取值范围为m∈(1,5).
解法二:由于直线过定点(0,1),而直线与椭圆总有公共点,所以定点(0,1)必在椭圆内部或边界上,由点与椭圆的位置关系的充要条件易求.
另解:
由椭圆方程及椭圆的焦点在x轴上知:0<m<5.
又∵直线与椭圆总有公共点.
∴ 直线所经过的定点(0,1)必在椭圆内部或边界上.
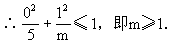
故m的取值范围为m∈(1,5),
小结:解法一由直线与圆锥曲线的位置关系的充要条件求,思路易得,但计算量大;解法二由点与圆锥曲线的位置关系的充要条件求,思路灵活,且简捷.

称,求m的取值范围.
解法一:利用判别式法.
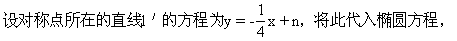
并整理得:
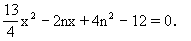
∵直线l′与椭圆C相交于两点,
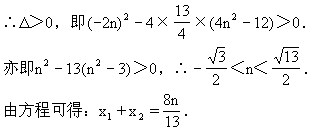
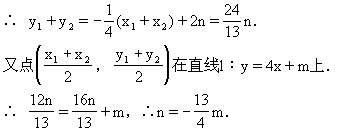
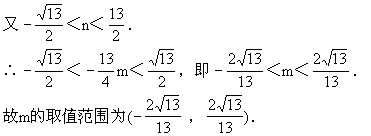
解法二:利用内点法.
设两对称点为P1(x1,y1),P2(x2,y2),P1P2的中点为M(x0,y0),
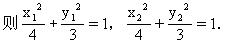
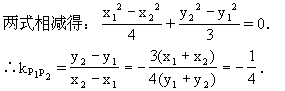
∴y1+y2=3(x1+x2).(1)
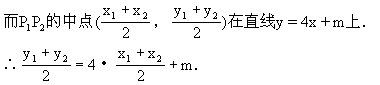
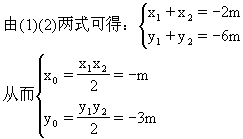
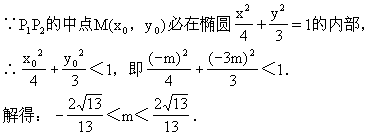
小结:本例中的判别式法和内点法,是解决圆锥曲线上存在两点关于直线的对称的一般方法,类似可解抛物线、双曲线中的对称问题.
练习1:(1)直线过点A(0,1)且与抛物线y2=x只有一个公共点,这样的直线有几条?
(2)过点P(2,0)的直线l与双曲线x2-y2=1只有一个公共点,这样的直线有几条?
由学生练习后口答:(1)3条,两条切线和一条平行于x轴的直线;(2)2条,注意到平行于渐近线的直线与双曲线只有一个交点,故这样的直线也只有2条.
练习2:求曲线C∶x2+4y2=4关于直线y=x-3对称的曲线C′的方程.
由教师引导方法,学生演板完成.解答为:
设(x′,y′)是曲线C上任意一点,且设它关于直线y=x-3的对称点为(x,y).
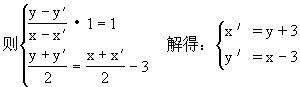
又(x′,y′)为曲线C上的点,
∴(y+3)2+4(x-3)2=4.
∴曲线C的方程为:4(x-3)2+(y+3)2=4.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com