2、在△ABC中，设命题p: 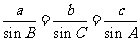,命题q: △ABC是等边三角形，那么命题p是命题q的(　 )

A.充分不必要条件　　 B.必要不充分条件　　　 C.充要条件　　 D.既不充分也不必要条件

总结：对于给出条件是边角关系混合在一起的问题，一般地，应运用正弦定理和余弦定理，要么把它统一为边的关系，要么统一为角的关系。再利用三角形的有关知识进行转化，化简

ⅲ综合运用

例2：已知圆O的半径为R,它的内接△ABC满足2R()=()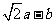sinB,求△ABC面积的最大值

例3：设a.b.c是△ABC中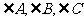的对边，其外接圆半径为1，且(sinA+sinB+sinC)(sinB+sinC-sinA)=3sinBsinC,b,c是方程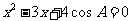的两根(b>c)

①　　 求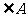的度数及a,b,c的值

②　　 判断△ABC的形状，并求其内切圆的半径

Ⅱ小结

作业：苏大对应部分

3、能解决一些有关三角形的综合问题；

Ⅱ能力目标：能通过本节课的学习，培养学生一定的归纳总结及迁移能力

教学重点：正余弦定理的合理运用

教学难点：正确选择正余弦定理

教学手段：多媒体教学

教学过程：

Ⅰ复习回顾：

ⅰ解斜三角形的基本类型及解法：

⑴已知两角和一边(如：A,B,及边c)解法：正弦定理

⑵已知两边及夹角(如：a,b及C)解法：余弦定理

⑶已知两边及一边的对角(如：a,b及A)解法：正弦定理。注意解的个数

练习：不解三角形，确定下列判断中正确的是(　 )

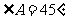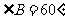C.a=6,b=9, ,有两解；　　　 D.b=9,c=10, ,无解

⑷已知三边(如：a,b.c) 解法：余弦定理

总结：在解斜三角形时，三条边，三个角，已知其中三个元素(至少有一条边)就可以求其他元素。

ⅱ判断三角形的形状

常见的一些结论：

①　　 若⊿ABC为锐角三角形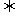cosA>0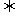

②　　 若⊿ABC为钝角三角形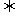cosA<0

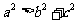
③　　 若⊿ABC为直角三角形cosA=0

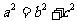
④　　 若sin2A=sin2B,则A=B, 或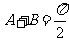

例1：△ABC中，若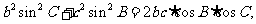试判断三角形的形状

练习：1、在△ABC中，若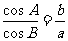，则三角形是_________三角形；

2、能根据正余弦定理判断处三角形的形状；

5．检验结果行不行：对题目的所求结果进行检验，并对其结果进行物理意义上的表述和讨论。

此外，在解题过程中，要特别注意以下两点。

第一：对物体受力分析要全面，切忌漏力，要时刻关注电场力F＝qE，洛伦兹力F＝qvB在具体情景中随物体带电属性(电荷的正负)、运动状态(速度的大小和方向)的变化特点；

第二，力学的规律普遍适于力电综合问题的求解。利用能量观点分析求解时，不再拘泥于机械能间转化，要总揽全局，站在更高的角度来分析能量间的转化途径与转化方向，从而列出能量转化和守恒方程。

4．找规律、列方程：在对物理状态和物理过程深刻把握的基础上，寻找题设条件与所求未知物理量的联系，从力的观点或能量的观点，依物理规律(牛顿第二定律，能的转化与守恒，动量守恒定律等)列出方程求解；

3．分析状态和过程：对全过程层层分析，对每一个中间过程的特点规律加以研究，分析挖掘相邻过程中的临界状态和临界条件，寻找各阶段物理量的变化与联系；

2．选对象，建模型：通过对整个题目的情景把握，选取研究对象，通过抽象、概括或类比等效的方法建立相应的物理模型，并对其进行全面的受力分析；

力电综合类题目以力和能量为主线，通过力学知识和电学知识的串接渗透作为背景，进行综合命题，其解题思路和解题步骤如下。

1．画草图，想情景：审题是解题的首要环节，在全面审视题目的条件，解答要求的基础上，对题目的信息进行加工处理，画出示意图(包括受力分析图，运动情景图和轨迹图)，借助图示建立起清晰的物理情景；

(三)创新试题

1．解析：(1)由题意，要使两电荷总是以相同的速度通过y轴，磁场中的电荷必须垂直y轴通过，因P点电荷为正电荷，故起始运动方向竖直向上，且一个周期内P点电荷两次以相反的速度通过y轴。

由牛顿运动定律得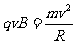　　 电荷在磁场中运动的周期为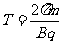

所以电场变化周期和点电荷圆周运动周期相同，即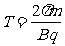

P点电荷经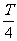第一次通过y轴，Q点电荷在电场中往复直线运动，

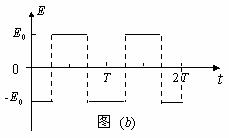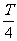在0-内有qE₀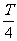=mv　 而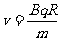

可求得，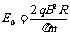

起始方向为-x方向。

(2)见图

2．解析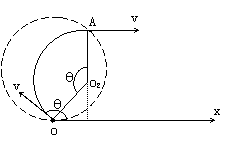：(1)当θ=60°时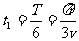，；当θ=90°时，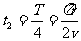

(2)如右图所示，因∠OO₂A=θ故O₂A⊥Ox

而O₂A与电子射出的速度方向垂直，可知电子射出方向一定与Ox轴方向平行，即所有的电子射出圆形磁场时，速度方向沿x轴正向。

(3)上述的粒子路径是可逆的，(2)中从圆形磁场射出的这些速度相同的电子再进入一相同的匀强磁场后，一定会聚焦于同一点，磁场的分布如下图所示。

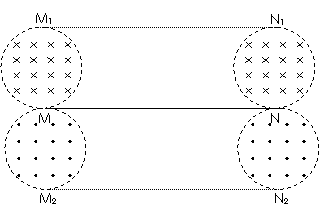注：①四个圆的半径相同，半径r的大小与磁感应强度的关系是r=mv₀/qB；

②下方的两圆形磁场与上方的两圆形磁场位置关于MN对称且磁场方向与之相反；

③只要在矩形区域M₁N₁N₂M₂内除图中4个半圆形磁场外无其他磁场，矩形M₁N₁N₂M₂区域外的磁场均可向其余区域扩展。

(二)解答题

1．解析：(1)设液珠的电量为q，质量为m

由题意知，当液珠在C点时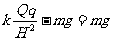　 解得比荷为：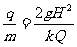

(2)当液珠速度最大时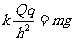　　　 　　　 得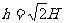

(3)设BC间的电势差大小U_CB，由题意得U_CB=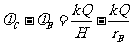

对由释放至液珠到达最高点(速度为零)的全过程应用动能定理得

qU_CB-mg(r_B-H)=0　　 即q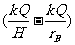-mg(r_B-H)=0

将第(1)问的结果代入化简r_B²-3Hr_B+2H²=0　 解得r_B=2H　 r_B′=H(舍去)

2．解析：该同学所得结论有不完善之处。

为使小球始终沿水平面运动，电场力在竖直方向的分力必须小于等于重力，

即：qEsinθ≤mg　　　 所以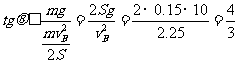

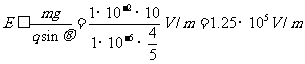　即：7.5×10⁴V/m＜E≤1.25×10⁵V/m

3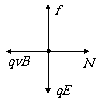．解析：小球在沿杆向下运动时，受力情况如图所示：

在水平方向：N=qvB　 所以摩擦力f=μN=μqvB

当小球做匀速运动时：qE=f=μqv_bB

小球在磁场中做匀速圆周运动时，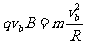

又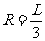，所以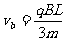

小球从a运动到b的过程中，由动能定理得：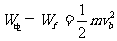

而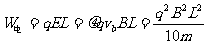　 所以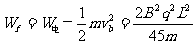

则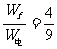

4．解析：(1)粒子在电场中被加速，由动能定理得

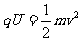
α粒子在磁场中偏转，则牛顿第二定律得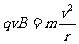

联立解得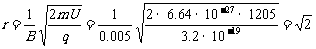(m)

(2)由几何关系可得，α粒子恰好垂直穿过分界线，故正确图象为

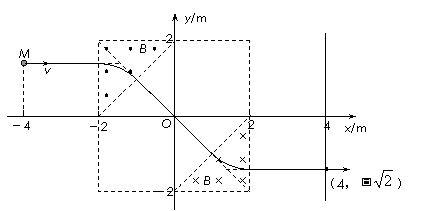
(3)带电粒子在磁场中的运动周期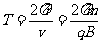

α粒子在两个磁场中分别偏转的弧度为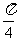，在磁场中的运动总时间

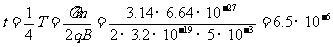(s)

5．解答：(1)用左手定则判断出：磁场方向为－x方向或－y方向。

(2)在未加匀强磁场时，带电小球在电场力和重力作用下落到P点，设运动时间为t，小球自由下落，有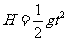

小球沿x轴方向只受电场力作用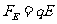

小球沿x轴的位移为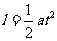　 小球沿x轴方向的加速度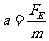

联立求解，得：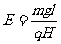

(3)带电小球在匀强磁场和匀强电场共存的区域运动时，洛仑兹力不做功

电场力做功为W_E=qEL

重力做功为W_G=mgH

设落到N点速度大小为v，根据动能定理有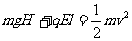

解得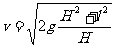

6．解答：(1)不加电场时，小球运动的时间为t，水平射程为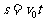，下落高度h=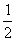gt²

加电场后小球在空间的运动时为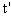，小球运动的加速度为a

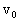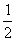2s=　　h=at^,2

解得: t′=2t　 a=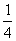g 由此可以判断:电场方向竖直向下。

并解得电场力的大小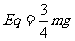　　 即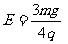

(2)加上匀强电场后，小球做匀速直线运动，故小球所受重力、电场力和洛仑兹力三个力而处于平衡，由于重力大于电场力，所以洛仑兹力方向竖直向上。

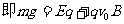
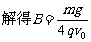　 用左手定则可得：磁场方向垂直于纸面向外