
1.在△ABC中,A:B:C=1:2:3,则a:b:c等于 ▲ .
20、已知二次函数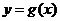 的导函数的图像与直线
的导函数的图像与直线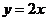 平行,且
平行,且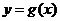 在
在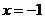 处取得极小值
处取得极小值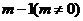 .设
.设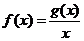 .(1)若曲线
.(1)若曲线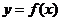 上的点
上的点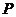 到点
到点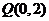 的距离的最小值为
的距离的最小值为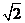 ,求
,求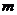 的值;(2)
的值;(2)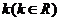 如何取值时,函数
如何取值时,函数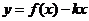 存在零点,并求出零点.
存在零点,并求出零点.
19、将数列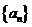 中的所有项按第一行排3项,以下每一行比上一行多一项的规则排成如下数表:
中的所有项按第一行排3项,以下每一行比上一行多一项的规则排成如下数表: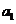


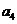
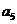
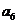
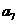

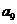
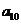
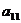
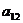
……
记表中的第一列数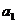 ,
, ,
,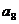 ,… ,构成数列
,… ,构成数列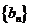 . (Ⅰ)设
. (Ⅰ)设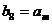 ,求
,求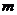 的值;(Ⅱ)若
的值;(Ⅱ)若 ,对于任何
,对于任何 ,都有
,都有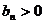 ,且
,且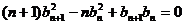 .求数列
.求数列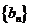 的通项公式;(Ⅲ)对于(Ⅱ)中的数列
的通项公式;(Ⅲ)对于(Ⅱ)中的数列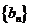 ,若上表中每一行的数按从左到右的顺序均构成公比为
,若上表中每一行的数按从左到右的顺序均构成公比为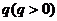
18、某校学生社团心理学研究小组在对学生上课注意力集中情况的调查研究中,发现其注
意力指数 与听课时间
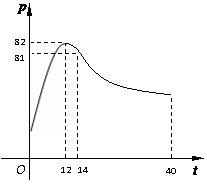
与听课时间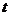 之间的关系满足如图所示的曲线.当
之间的关系满足如图所示的曲线.当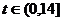 时,曲线是二次函数图象的一部分,当
时,曲线是二次函数图象的一部分,当 时,曲线是函数
时,曲线是函数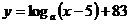 (
(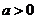 且
且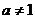 )图象的一部分.根据专家研究,当注意力指数
)图象的一部分.根据专家研究,当注意力指数 大于80时听课效果最佳.
大于80时听课效果最佳.
 (1) 试求
(1) 试求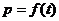 的函数关系式;(2) 老师在什么时段内安排核心内容能使得学生听课效果最佳?请说明理由.
的函数关系式;(2) 老师在什么时段内安排核心内容能使得学生听课效果最佳?请说明理由.
17、已知圆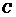 方程为:
方程为: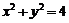 .
.
(Ⅰ)直线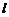 过点
过点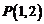 ,且与圆
,且与圆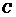 交于
交于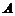 、
、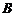 两点,若
两点,若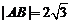 ,求直线
,求直线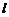 的方程;
的方程;
(Ⅱ)过圆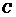 上一动点
上一动点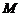 作平行于
作平行于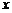 轴的直线
轴的直线 ,设
,设 与
与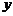 轴的交点为
轴的交点为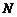 ,若向量
,若向量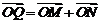 ,求动点
,求动点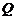 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.
16、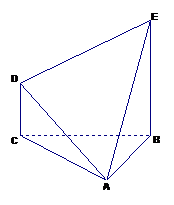 何体ABCDE中,
何体ABCDE中,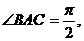 DC⊥平面ABC,EB⊥平面ABC,AB=AC=BE=2,CD=1,(I)求证:;
DC⊥平面ABC,EB⊥平面ABC,AB=AC=BE=2,CD=1,(I)求证:;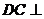 平面ABE;(II)设平面ABE与平面ACD的交线为直线l,求证:
平面ABE;(II)设平面ABE与平面ACD的交线为直线l,求证: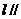 平面BCDE;(III)设F是BC的中点,求证:平面AFD⊥平面AFE。
平面BCDE;(III)设F是BC的中点,求证:平面AFD⊥平面AFE。
15、已知向量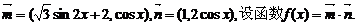
(I)求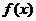 的最小正周期与单调递减区间。(II)在△ABC中,a、b、c、分别是角A、B、C的对边,若
的最小正周期与单调递减区间。(II)在△ABC中,a、b、c、分别是角A、B、C的对边,若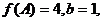 △ABC的面积为
△ABC的面积为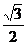 ,求
,求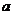 的值。
的值。
14.平面几何中有命题“正三角形内任意一点到三边的距离之和等于定值,大小为边长的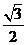 倍”,请你写出此命题在立体几何中类似的真命题____________________________.
倍”,请你写出此命题在立体几何中类似的真命题____________________________.
13.对于函数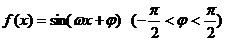 ,以下列四个命题中的两个为条件,余下的两个为结论,写出你认为正确的一个命题 (序号表示)
。
,以下列四个命题中的两个为条件,余下的两个为结论,写出你认为正确的一个命题 (序号表示)
。
①函数f (x)图像关于直线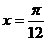 对称; ②函数f (x)在区间
对称; ②函数f (x)在区间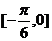 上是增函数;③函数f (x)图像关于点
上是增函数;③函数f (x)图像关于点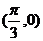 对称; ④函数f (x)周期为
对称; ④函数f (x)周期为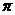 .
.
11.过抛物线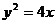 焦点的直线交抛物线于A、B两点,过B点作抛物线的准线
焦点的直线交抛物线于A、B两点,过B点作抛物线的准线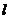 的垂线,垂足为C,已知点A(4,4),则直线AC的方程为
12.右图给出的是计算
的垂线,垂足为C,已知点A(4,4),则直线AC的方程为
12.右图给出的是计算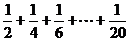 的值的一个流程图,其中判断
的值的一个流程图,其中判断
框内应填入的条件是____________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com