
20、(1)设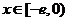 ,则
,则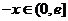 ,所以
,所以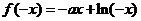
又因为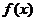 是定义在
是定义在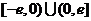 上的奇函数,所以
上的奇函数,所以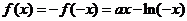
故函数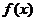 的解析式为
的解析式为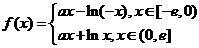
(2)证明:当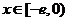 且
且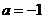 时,
时,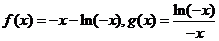 ,设
,设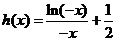 ,因为
,因为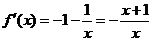 ,所以当
,所以当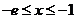 时,
时,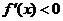 ,此时
,此时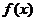 单调递减;当
单调递减;当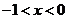 时,
时,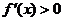 ,此时
,此时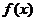 单调递增,所以
单调递增,所以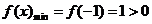 , 又因为
, 又因为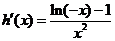 ,所以当
,所以当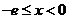 时,
时,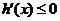 ,此时
,此时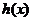 单调递减,所以
单调递减,所以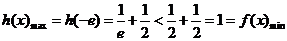
所以当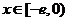 时,
时,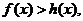 即
即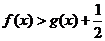
(3)解:假设存在实数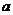 ,使得当
,使得当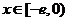 时,
时,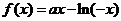 有最小值是3,则
有最小值是3,则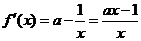
(ⅰ)当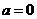 ,
,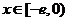 时,
时,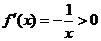 .
.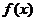 在区间
在区间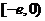 上单调递增,
上单调递增,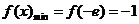 ,不满足最小值是3
,不满足最小值是3
(ⅱ)当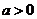 ,
,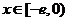 时,
时,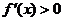 ,
,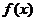 在区间
在区间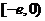 上单调递增,
上单调递增,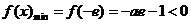 ,也不满足最小值是3
,也不满足最小值是3
(ⅲ)当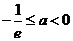 ,由于
,由于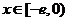 ,则
,则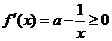 ,故函数
,故函数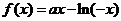 是
是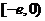 上的增函数.
上的增函数.
所以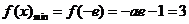 ,解得
,解得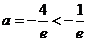 (舍去)
(舍去)
(ⅳ)当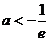 时,则
时,则
当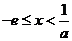 时,
时,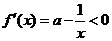 ,此时函数
,此时函数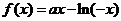 是减函数;
是减函数;
当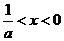 时,
时,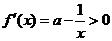 ,此时函数
,此时函数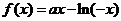 是增函数.
是增函数.
所以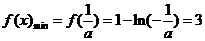 ,解得
,解得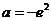
综上可知,存在实数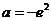 ,使得当
,使得当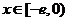 时,
时,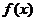 有最小值3
有最小值3
19、解:(1)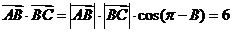 ①
①
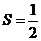
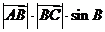 ②;由①、②得,
②;由①、②得,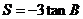 .
.
由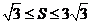 可得,
可得,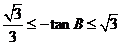 ,又
,又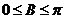 ,所以
,所以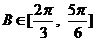 .
.
(2)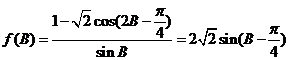 ,
,
因为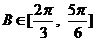 ,所以
,所以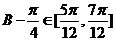 ,
,
当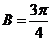 时,
时,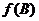 取最大值
取最大值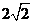 ;当
;当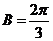 或
或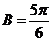 时,
时,
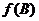 取最小值
取最小值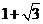 .… 综上,所求函数的值域为
.… 综上,所求函数的值域为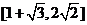 .
.
18、(Ⅰ)设日销量为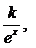 则
则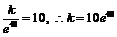 . 则日售量为
. 则日售量为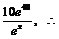 日利润
日利润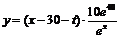 .
. 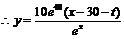 ,其中
,其中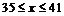 .
.
(Ⅱ)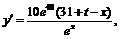 令
令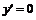 得
得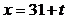 .
.
①当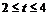 时,
时,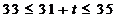 .
.  当
当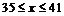 时,
时,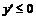 .
.
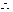 当
当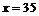 时,
时,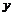 取最大值,最大值为
取最大值,最大值为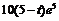 .
.
②当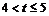 时,
时,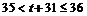 ,函数
,函数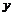 在
在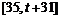 上单调递增,在
上单调递增,在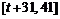 上单减.
上单减.  当
当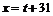 时,
时,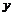 取最大值
取最大值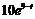 .
.
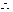 当
当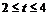 时,
时,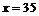 时,日利润最大值为
时,日利润最大值为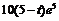 元
元
当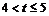 时,
时,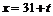 时,日利润最大值为
时,日利润最大值为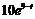 元.
元.
17.解: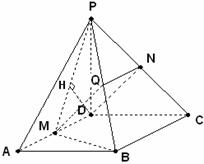 (1)证明:取PB中点Q,连结MQ、NQ,因为M、N分别是棱AD、PC中点,所以
(1)证明:取PB中点Q,连结MQ、NQ,因为M、N分别是棱AD、PC中点,所以
QN//BC//MD,且QN=MD,于是DN//MQ.
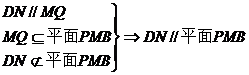 .
.
(2)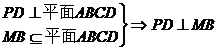
又因为底面ABCD是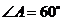 、边长为
、边长为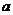 的菱形,且M为AD中点,
的菱形,且M为AD中点,
所以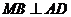 .
.
又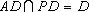
所以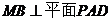 .
.
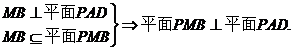
(3)因为M是AD中点,所以点A与D到平面PMB等距离.
过点D作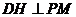 于H,由(2)平面PMB
于H,由(2)平面PMB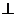 平面PAD,所以
平面PAD,所以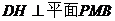 .
.
故DH是点D到平面PMB的距离.
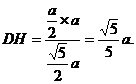
 所以点A到平面PMB的距离为
所以点A到平面PMB的距离为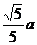 .
.
16.解:(1)A中2张钱币取1张,有2种情况, B中3张钱币取1张,有3种情况,
∴互换一次有2´3 = 6种情况,其中10元币恰是一张的情况有3种,
∴A袋中10元钱币恰是一张的概率为P1
=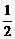 .答略
.答略
(2)A袋中恰有一张10元币的概率为P1 = 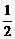 ;A袋中恰有两张10元币的概率为P2 =
;A袋中恰有两张10元币的概率为P2 = 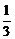 ;
;
∴ A袋中10元钱币至少是一张的概率P = P1 + P2
= 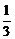 +
+ 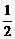 =
= 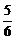 .
.
另解:. A袋中恰有0张10元币的概率为P0
= 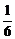 ,
,
∴A袋中10元钱币至少是一张的概率P = 1 – P0 = 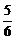 .答略.
.答略.
15、(Ⅰ)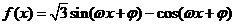
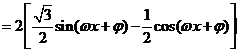
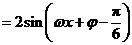 .
.
因为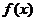 为偶函数,所以对
为偶函数,所以对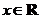 ,
,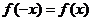 恒成立,
恒成立,
因此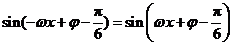 .
.
即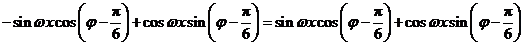 ,
,
整理得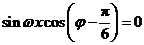 .因为
.因为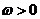 ,且
,且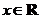 ,所以
,所以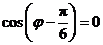 .
.
又因为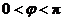 ,故
,故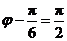 .所以
.所以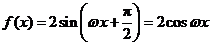 .
.
由题意得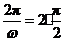 ,所以
,所以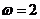 .故
.故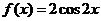 .因此
.因此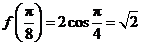 .
.
(Ⅱ)将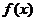 的图象向右平移
的图象向右平移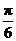 个单位后,得到
个单位后,得到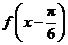 的图象,再将横坐标变为原来的4倍得到
的图象,再将横坐标变为原来的4倍得到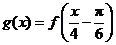 ,所以
,所以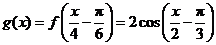 .
.
当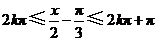 (
(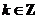 ),即
),即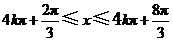 (
(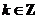 )时,
)时,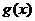 单调递减,因
单调递减,因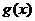 在
在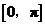 的单调递减区间
的单调递减区间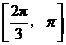 .
.
1.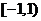 ; 2.
; 2.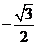 ;
3.
;
3.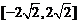 ;
4.充分不必要; 5.
;
4.充分不必要; 5.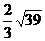 ;6.
;6.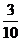 ; 7.
; 7.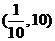 ; 8.1
9.
; 8.1
9.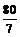 ; 10.①③ ; 11.
; 10.①③ ; 11.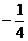 ; 12.
; 12.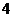 ;
13.
;
13.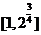 ; 14.
; 14.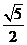 .
.
20.(本小题满分16分)
已知函数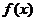 是定义在
是定义在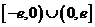 上的奇函数,当
上的奇函数,当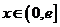 时,
时, 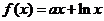 (其中e是自然界对数的底,
(其中e是自然界对数的底,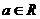 )(1)求
)(1)求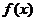 的解析式;
的解析式;
(2)设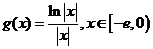 ,求证:当
,求证:当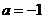 时,
时,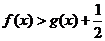 ;
;
(3)是否存在实数a,使得当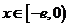 时,
时,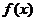 的最小值是3 ?如果存在,求出实数a的值;如果不存在,请说明理由。
的最小值是3 ?如果存在,求出实数a的值;如果不存在,请说明理由。
掘港中学高三数学期中复习自主训练题
19.(本小题满分15分)
已知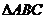 的面积
的面积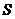 满足
满足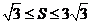 ,且
,且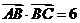 .(1)求角
.(1)求角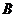 的取值范围;
的取值范围;
(2)求函数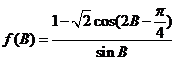 的值域.
的值域.
18.某工厂生产某种儿童玩具,每件玩具的成本为30元,并且每件玩具的加工费为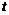 元(其中
元(其中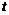 为常数,且
为常数,且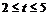 ),设该工厂每件玩具的出厂价为
),设该工厂每件玩具的出厂价为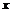 元(
元(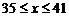 ),根据市场调查,日销售量与
),根据市场调查,日销售量与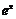 (
(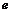 为自然对数的底数)成反比例,当每件玩具的出厂价为40元时,日销售量为10件.(Ⅰ)求该工厂的日利润
为自然对数的底数)成反比例,当每件玩具的出厂价为40元时,日销售量为10件.(Ⅰ)求该工厂的日利润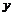 (元)与每件玩具的出厂价
(元)与每件玩具的出厂价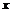 元的函数关系式;
元的函数关系式;
(Ⅱ)当每件玩具的日售价为多少元时,该工厂的利润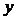 最大,并求
最大,并求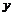 的最大值.
的最大值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com