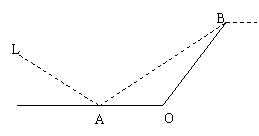
17. 某城市有一条公路，自西向东经过A点到市中心O点后转向东北方向OB，现要修建一条铁路L，

L在OA上设一站A，在OB上设一站B，铁路在AB部分为直线段，现要求市中心O与AB的距离为10 km，

问把A、B分别设在公路上离中心O多远处才能使|AB|最短?并求其最短距离.

16. 如图, 在直三棱柱ABC－A₁B₁C₁中,∠ACB＝90°，E、F、G分别是AA₁、AC、BB₁的中点，且CG⊥C₁G.

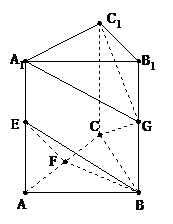(Ⅰ)求证：CG∥平面BEF；网

(Ⅱ)求证：平面BEF⊥平面A₁C₁G.

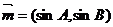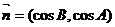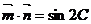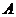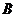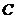15. 已知向量，，，其中、、为△ABC的内角.

(Ⅰ)求角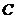的大小；

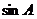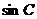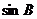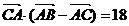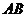(Ⅱ)若，，成等差数列，且，求的长.

14. 设函数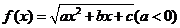的定义域为D，

若所有点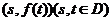构成一个正方形区域，则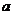的值为__________；

13. 在正三棱锥A－BCD中，E、F是AB、BC的中点，EF⊥DE，若BC＝a，

则正三棱锥A－BCD的体积为___________；

12. 设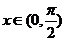，则函数(的最小值是__________；

11. 已知函数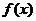,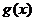满足,,,,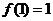

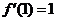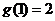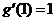则函数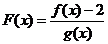的图象在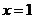处的切线方程为_________________；

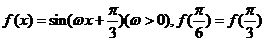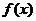10. 已知，且在区间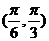有最小值，无最大值，则____；

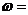9. 椭圆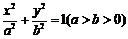的一个焦点为F，点P在椭圆上，

且△OPF(O为坐标原点)为等边三角形，则椭圆的离心率e＝_________；

8. 学习合情推理后，甲、乙两位同学各举一个例子．

甲：由“若三角形周长为l，面积为S, 则其内切圆半径r =”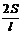

类比可得“若三棱锥表面积为S，体积为V，则其内切球半径r =”；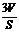

乙：由“若直角三角形两直角边长分别为a、b，则其外接圆半径r =”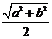

类比可得“若三棱锥三条侧棱两两垂直， 侧棱长分别为a、b、c，则其外接球半径r =”.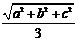

这两位同学类比得出的结论正确的是__________；