
5.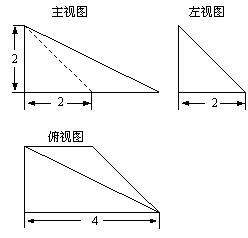 已知一个空间几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是 ▲ cm3.
已知一个空间几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是 ▲ cm3.

4.已知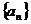 为等差数列,若
为等差数列,若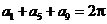 ,则
,则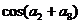 的值为 ▲ .
的值为 ▲ .
3.若函数 的图象的相邻两条对称轴的距离是
的图象的相邻两条对称轴的距离是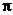 ,则
,则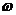 的值为 ▲ .
的值为 ▲ .
2.若复数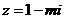 (
(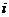 为虚数单位,
为虚数单位,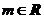 ),若
),若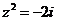 ,则复数
,则复数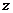 的虚部为 ▲ .
的虚部为 ▲ .
1.为了检查某超市货架上的奶粉是否含有三聚氰胺,要从编号依次为01到50的袋装奶粉中抽取5袋进行检验,现将50袋奶粉按编号顺序平均分成5组,用每组选取的号码间隔一样的系统抽样方法确定所选取的 袋奶粉的编号,若第4组抽出的号码为36,则第1组中用抽签的方法确定的号码是
▲ .
袋奶粉的编号,若第4组抽出的号码为36,则第1组中用抽签的方法确定的号码是
▲ .
20、(16分)已知函数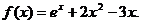
(1)求曲线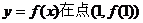 处的切线方程;
处的切线方程;
(2)求证函数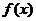 在区间[0,1]上存在唯一的极值点,并用二分法求函数取得极值时相应x的近似值(误差不超过0.2);(参考数据e≈2.7,
在区间[0,1]上存在唯一的极值点,并用二分法求函数取得极值时相应x的近似值(误差不超过0.2);(参考数据e≈2.7,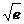 ≈1.6,e0.3≈1.3)
≈1.6,e0.3≈1.3)
(3)当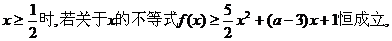 试求实数
试求实数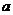 的取值范围.
的取值范围.
江苏省南通市2010届四星级高中内部交流卷
19、(16分)已知直线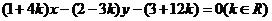 所经过的定点
所经过的定点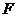 恰好是椭圆
恰好是椭圆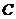 的一个焦点,且椭圆
的一个焦点,且椭圆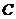 上的点到点
上的点到点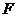 的最小距离为2.
的最小距离为2.
(1)求椭圆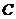 的标准方程;
的标准方程;
(2)已知圆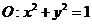 ,直线
,直线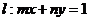 . 试证明:当点
. 试证明:当点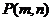 在椭圆
在椭圆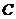 上运动时,直线
上运动时,直线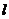 与圆
与圆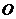 恒相交;并求直线
恒相交;并求直线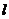 被圆
被圆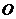 所截得的弦长的取值范围.
所截得的弦长的取值范围.
18、(15分)某工厂生产某种儿童玩具,每件玩具的成本为30元,并且每件玩具的加工费为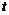 元(其中
元(其中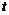 为常数,且
为常数,且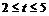 ),设该工厂每件玩具的出厂价为
),设该工厂每件玩具的出厂价为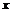 元(
元(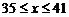 ),根据市场调查,日销售量与
),根据市场调查,日销售量与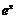 (
(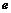 为自然对数的底数)成反比例,当每件玩具的出厂价为40元时,日销售量为10件.
为自然对数的底数)成反比例,当每件玩具的出厂价为40元时,日销售量为10件.
(1)求该工厂的日利润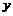 (元)与每件玩具的出厂价
(元)与每件玩具的出厂价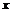 元的函数关系式;
元的函数关系式;
(2)当每件玩具的日售价为多少元时,该工厂的利润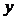 最大,并求
最大,并求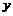 的最大值.
的最大值.
15(14分)、已知: 命题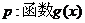 的图象与函数
的图象与函数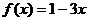 的图象关于直线
的图象关于直线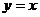 对称,且
对称,且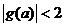 .命题
.命题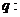 集合
集合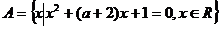 ,
,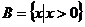 ,且
,且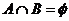 .求实数
.求实数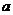 的取值范围,使命题
的取值范围,使命题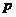 、
、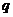 有且只有一个是真命题.
有且只有一个是真命题.
16(14分)、在等差数列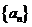 中,
中,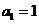 ,前
,前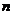 项和
项和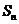 满足条件
满足条件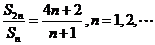 ,
,
(1)求数列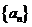 的通项公式;
的通项公式;
(2)记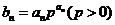 ,求数列
,求数列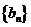 的前
的前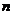 项和
项和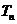 。
。
17.(本题满分14分)在长方体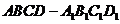 中,
中,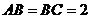 ,过
,过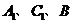 三点的的平面截去长方体的一个角后.得到如图所示的几何体
三点的的平面截去长方体的一个角后.得到如图所示的几何体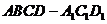 ,且这个几何体的体积为
,且这个几何体的体积为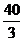 .
.
(1)求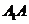 的长;
的长;
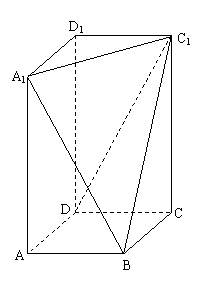 (2)在线段
(2)在线段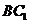 上是否存在点
上是否存在点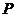 ,使直线
,使直线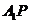 与
与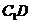 垂直,如果存在,求线段
垂直,如果存在,求线段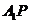 的长,如果不存在,请说明理由.
的长,如果不存在,请说明理由.
14、已知定义在R上的函数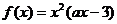 ,若函数
,若函数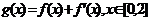 ,在x=0处取得最大值,则正数a的范围 ▲ .
,在x=0处取得最大值,则正数a的范围 ▲ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com