
8.已知函数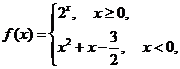 若
若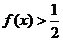 ,则
,则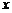 的取值范围是 ▲ .
的取值范围是 ▲ .
7.已知函数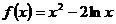 ,则
,则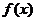 的最小值为 ▲
.
的最小值为 ▲
.
6.若函数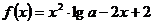 在区间
在区间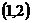 内有且只有一个零点,那么实数
内有且只有一个零点,那么实数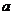 的取值范围是 ▲__.
的取值范围是 ▲__.
5.函数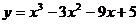 的单调递减区间是______▲________.
的单调递减区间是______▲________.
4.已知函数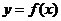 的图象在点
的图象在点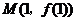 处的切线方程是
处的切线方程是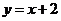 ,
,
则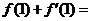 ▲ .
▲ .
3.设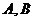 是非空集合,定义:
是非空集合,定义: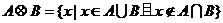 .已知
.已知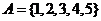 ,
,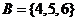 ,则
,则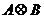 为__▲___.
为__▲___.
2.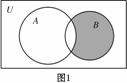 函数
函数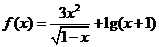 的定义域为 ___▲ .
的定义域为 ___▲ .
1.如图1所示,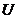 是全集,A、B是
是全集,A、B是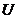 的子集,则阴影部分所表示的集合是_ _▲______.
的子集,则阴影部分所表示的集合是_ _▲______.
15(本题满分14分)设命题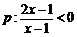 ,命题
,命题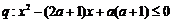 ,若p是q的充分不必要条件,求实数
,若p是q的充分不必要条件,求实数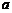 的取值范围.
的取值范围.
解:由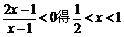 ,设集合
,设集合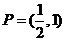
由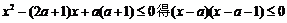
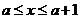 ,设集合
,设集合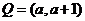
p是q的充分不必要条件得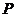 是
是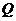 的真子集,故
的真子集,故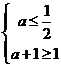 得
得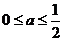
16(本题满分14分)
已知函数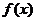 =
=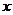 +
+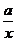 (x>0), a为常数,且
(x>0), a为常数,且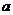
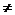 0.
0.
(1)研究函数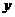 =
=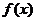 的单调性,并说明理由;
的单调性,并说明理由;
(2)如果函数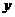 =
=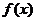 的值域为
的值域为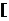 6,+∞
6,+∞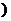 ,求
,求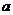 的值.
的值.
解:(1)由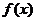 =
=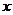 +
+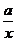 得
得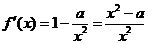 ,
2分
,
2分
当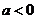 时,
时,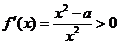 恒成立,
恒成立,
所以函数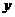 =
=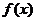 在
在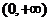 上为增函数;
4分
上为增函数;
4分
当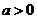 时,令
时,令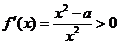 ,解得
,解得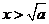 ,
,
令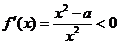 ,解得
,解得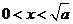 ,
,
所以函数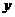 =
=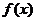 在
在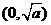 上为减函数;在
上为减函数;在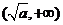 上为增函数。 7分
上为增函数。 7分
(2)由(1)可知当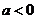 时,函数
时,函数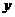 =
=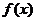 在
在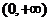 上为增函数,
上为增函数,
此时函数的值域为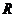 ,不合题意;
9分
,不合题意;
9分
当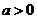 时,函数
时,函数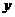 =
=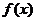 在
在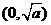 上为减函数;
上为减函数;
在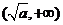 上为增函数,此时函数的值域为
上为增函数,此时函数的值域为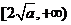 ,即
,即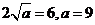 。
。
综上,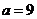 。
14分
。
14分
17(本题满分15分)已知定义域为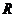 的函数
的函数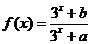 是奇函数.
是奇函数.
(1)求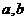 的值;
的值;
(2)讨论函数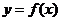 的单调性;
的单调性;
(3)若对任意的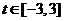 ,不等式
,不等式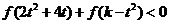 恒成立,求实数
恒成立,求实数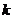 的取值范围.
的取值范围.
解:方法一:
由定义在R上的函数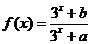 是奇函数得对一切
是奇函数得对一切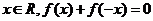 恒成立
恒成立
即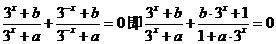 ,
,
整理得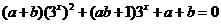 对任意
对任意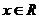 恒成立,
恒成立,
故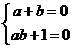 ,解得
,解得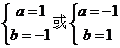 ,
,
又因为函数的定义域为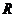 ,故
,故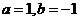 。
5分
。
5分
方法二:由题意可知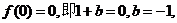 此时
此时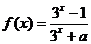 ,
,
又由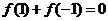 得
得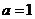 ,此时
,此时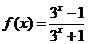 ,经检验满足
,经检验满足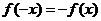 符合题意。
符合题意。
(不检验扣1分) 5分
(2)由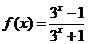 得
得
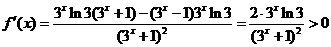 恒成立,
恒成立,
故函数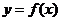 在R上为增函数。
10分
在R上为增函数。
10分
(3) 函数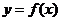 为奇函数且在R上为增函数
为奇函数且在R上为增函数
由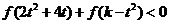 得
得
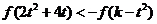
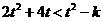 12分
12分
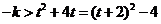 对一切
对一切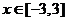 恒成立
恒成立
所以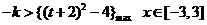
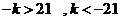 15分
15分
注:若选择用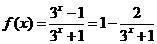 在R上为增函数,此时要用定义给出证明。
在R上为增函数,此时要用定义给出证明。
18(本题满分15分)某车间有200名工人,要完成6000件产品的生产任务,每件产品由3个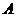 型零件和1个
型零件和1个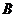 型零件配套组成.每个工人每小时能加工5个
型零件配套组成.每个工人每小时能加工5个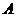 型零件或者1个
型零件或者1个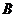 型零件,现在把这些工人分成两组同时工作(分组后人数不再进行调整),每组加工同一种型号的零件.设加工
型零件,现在把这些工人分成两组同时工作(分组后人数不再进行调整),每组加工同一种型号的零件.设加工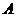 型零件的工人人数为
型零件的工人人数为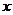 名(
名(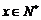 ).
).
(1)设完成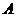 型零件加工所需时间为
型零件加工所需时间为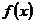 小时,完成B型零件加工所需时间为
小时,完成B型零件加工所需时间为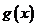 小时,写出
小时,写出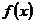 ,
,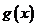 的解析式;
的解析式;
(2)当A、B两种零件全部加工完成,就算完成工作.全部完成工作所需时间为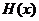 小时,写出
小时,写出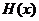 的解析式;
的解析式;
(3)为了在最短时间内完成工作,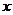 应取何值?
应取何值?
解:(1)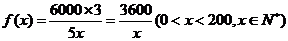 ,
2分
,
2分
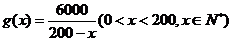 。
4分
。
4分
(2)令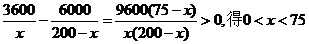
故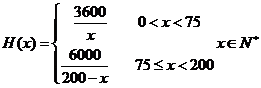 9分
9分
(3)即求函数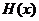 的最小值。当
的最小值。当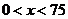 时,
时,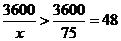 ,当
,当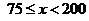 时,
时,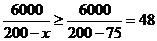 ,故当
,故当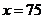 时
时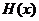 的最小值为
的最小值为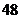 。
。
综上,为了在最短时间内完成工作,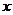 应取
应取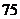 。
15分
。
15分
19(本题满分16分)已知函数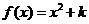
(1)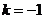 时,设,求
时,设,求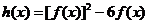 ,
,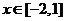 的最大值.
的最大值.
(2)若函数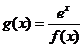 ,且
,且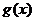 在区间(2,3)上不单调,求实数k的取值范围.
在区间(2,3)上不单调,求实数k的取值范围.
解(1)当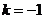 时,
时,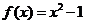 ,又
,又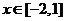 ,故
,故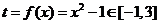
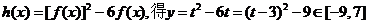 ,
,
也即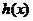 的最大值为7.此时
的最大值为7.此时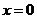 。
7分
。
7分
(2)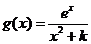 ,
,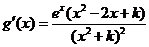 ,因为
,因为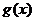 在区间(2,3)上不单调,故
在区间(2,3)上不单调,故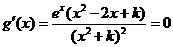 在区间(2,3)上有根,且不能有两个相等的根。
在区间(2,3)上有根,且不能有两个相等的根。
令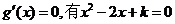
则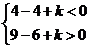 ,解得
,解得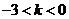 。
16分
。
16分
20(本题满分16分)已知函数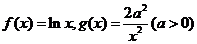 ,设
,设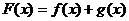 。
。
(1)求F(x)的单调区间;
(2)若以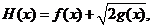 图象上任意一点
图象上任意一点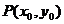 为切点的切线的斜率
为切点的切线的斜率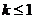 恒成立,求实数
恒成立,求实数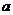 的最小值;
的最小值;
(3)是否存在实数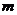 ,使得函数
,使得函数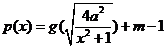 的图象与
的图象与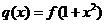 的图象恰好有四个不同的交点?若存在,求出
的图象恰好有四个不同的交点?若存在,求出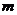 的取值范围,若不存在,说明理由。
的取值范围,若不存在,说明理由。
解.(1) 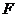
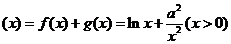
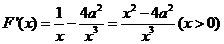
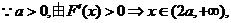
由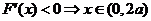 。
。
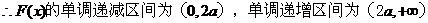 4分
4分
(2)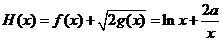 ,
,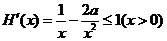 ,则
,则
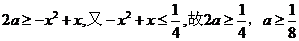 ,
,
所以实数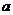 的最小值为
的最小值为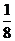 。
10分
。
10分
(3)若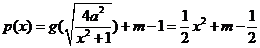 的图象与
的图象与
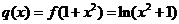 的图象恰有四个不同交点,
的图象恰有四个不同交点,
即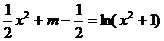 有四个不同的根,亦即
有四个不同的根,亦即
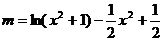 有四个不同的根。
有四个不同的根。
令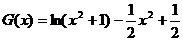 ,
,
则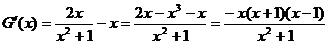 。
。
当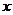 变化时
变化时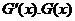 的变化情况如下表:
的变化情况如下表:
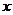 |
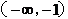 |
(-1,0) |
(0,1) |
(1,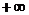 ) ) |
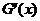 的符号 的符号 |
+ |
- |
+ |
- |
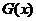 的单调性 的单调性 |
↗ |
↘ |
↗ |
↘ |
由表格知: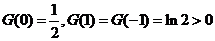 。
。
又因为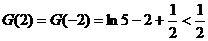 可知,当
可知,当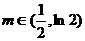 时,
时,
方程
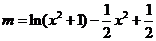 有四个不同的解.
有四个不同的解.
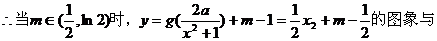
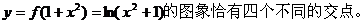 16分
16分
14.对于在区间[a,b]上有意义的两个函数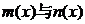 ,如果对于区间[a,b]中的任意x均有
,如果对于区间[a,b]中的任意x均有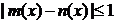 ,则称
,则称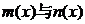 在[a,b]上是“密切函数”, [a,b]称为“密切区间”,若函数
在[a,b]上是“密切函数”, [a,b]称为“密切区间”,若函数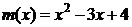 与
与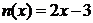 在区间[a,b]上是“密切函数”,则
在区间[a,b]上是“密切函数”,则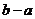 的最大值为 1
.
的最大值为 1
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com