
1.已知集合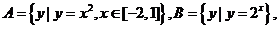 则
则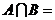 ▲ .
▲ .
24.(本题满分10分)
已知集合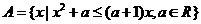 .
.
(Ⅰ)求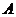 ;
;
(Ⅱ)若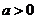 ,以
,以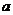 为首项,
为首项,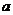 为公比的等比数列前
为公比的等比数列前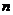 项和记为
项和记为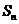 ,对于任意的
,对于任意的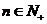 ,均有
,均有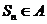 ,求
,求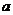 的取值范围.
的取值范围.
23.(本题满分10分)
已知数列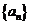 的前
的前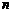 项和为
项和为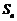 ,通项公式为
,通项公式为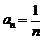 ,
,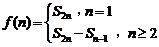 .
.
(Ⅰ)计算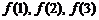 的值;
的值;
(Ⅱ)比较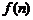 与1的大小,并用数学归纳法证明你的结论.
与1的大小,并用数学归纳法证明你的结论.
22.(本题满分10分)
设曲线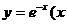 ≥0)在点M(t,
≥0)在点M(t, 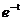 )处的切线
)处的切线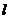 与x轴y轴所围成的三角形面积为
与x轴y轴所围成的三角形面积为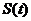 ,
,
求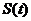 的解析式.
的解析式.
21.(本题满分10分)
求函数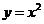 (
(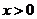 )与函数
)与函数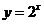 的图像所围成的封闭区域的面积.
的图像所围成的封闭区域的面积.
20.(本题满分16分)
已知函数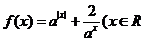 ,
,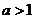 ).
).
(Ⅰ)求函数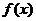 的值域;
的值域;
(Ⅱ)记函数g(x) = f
(-x),x∈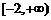 ,若g(x)的最小值与a无关,求a的取值范围;
,若g(x)的最小值与a无关,求a的取值范围;
(Ⅲ)若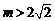 ,直接写出(不需给出演算步骤)关于x的方程f(x)=m
的解集.
,直接写出(不需给出演算步骤)关于x的方程f(x)=m
的解集.
数学Ⅱ(附加题)
19.(本题满分16分)
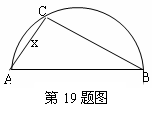
两镇A和B相距20km,现计划在两镇外以AB为直径的半圆弧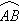 上选择一点C建造垃圾处理厂,其对镇区的影响度与所选地点到镇的的距离有关,对镇A和镇B的总影响度为镇A与镇B的影响度之和,记C点到镇A的距离为x km,建在C处的垃圾处理厂对镇A和镇B的总影响度为y,统计调查表明:垃圾处理厂对镇A的影响度与所选地点到镇A的距离的平方成反比,比例系数为4;对镇B的影响度与所选地点到镇B的距离的平方成反比,比例系数为k,当垃圾处理厂建在
上选择一点C建造垃圾处理厂,其对镇区的影响度与所选地点到镇的的距离有关,对镇A和镇B的总影响度为镇A与镇B的影响度之和,记C点到镇A的距离为x km,建在C处的垃圾处理厂对镇A和镇B的总影响度为y,统计调查表明:垃圾处理厂对镇A的影响度与所选地点到镇A的距离的平方成反比,比例系数为4;对镇B的影响度与所选地点到镇B的距离的平方成反比,比例系数为k,当垃圾处理厂建在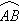 的中点时,对镇A和镇B的总影响度为0.065.
的中点时,对镇A和镇B的总影响度为0.065.
(Ⅰ)将y表示成x的函数;
(Ⅱ)讨论(Ⅰ)中函数的单调性,并判断弧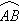 上是否存在一点,使建在此处的垃圾处理厂对镇A和镇B的总影响度最小?若存在,求出该点到镇A的距离;若不存在,说明理由.
上是否存在一点,使建在此处的垃圾处理厂对镇A和镇B的总影响度最小?若存在,求出该点到镇A的距离;若不存在,说明理由.
18.(本题满分15分)
已知分别以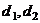 为公差的等差数列
为公差的等差数列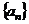 ,
,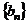 ,满足
,满足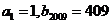 .
.
(Ⅰ)若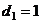 ,且存在正整数
,且存在正整数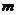 ,使得
,使得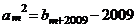 ,求
,求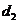 的最小值;
的最小值;
(Ⅱ)若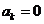 ,
,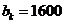 且数列
且数列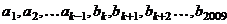 ,的前项
,的前项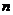 和
和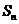 满足
满足
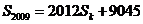 ,求
,求 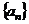 的通项公式.
的通项公式.
17.(本题满分15分)
已知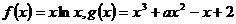 .
.
(Ⅰ)如果函数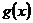 的单调递减区间为
的单调递减区间为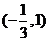 ,求函数
,求函数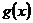 的解析式;
的解析式;
(Ⅱ)在(Ⅰ)的条件下,求函数y=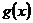 的图像在点
的图像在点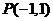 处的切线方程;
处的切线方程;
(Ⅲ)若不等式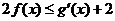 的解集为P,且
的解集为P,且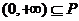 ,求实数
,求实数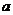 的取值范围.
的取值范围.
16.(本题满分14分)
已知定义在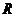 的函数
的函数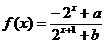 (
(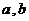 为实常数).
为实常数).
(Ⅰ)当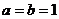 时,证明:
时,证明: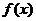 不是奇函数;
不是奇函数;
(Ⅱ)设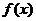 是奇函数,求
是奇函数,求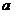 与
与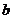 的值;
的值;
(Ⅲ)当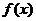 是奇函数时,证明对任何实数
是奇函数时,证明对任何实数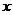 、c都有
、c都有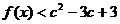 成立.
成立.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com