
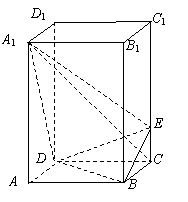
22.(本题满分10分)如图,正四棱柱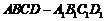 中,
中,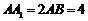 ,点
,点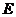 在
在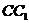 上且
上且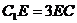 .
.
(Ⅰ)证明: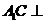 平面
平面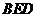 ;
;
(Ⅱ)求二面角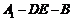 的大小.
的大小.
21.(1)(本题满分10分)设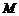 是把坐标平面上的点
是把坐标平面上的点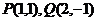 分别变换成点
分别变换成点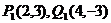 .
.
(Ⅰ)求矩阵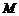 ;(Ⅱ)求椭圆
;(Ⅱ)求椭圆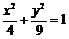 在
在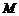 的作用下的新曲线的方程.
的作用下的新曲线的方程.
(2)(本题满分10分)已知椭圆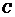 的极坐标方程为
的极坐标方程为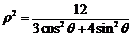 .
.
(1) 求曲线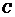 的普通方程;(2)若点
的普通方程;(2)若点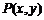 为曲线
为曲线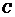 上任一点,求
上任一点,求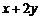 的取值范围.
的取值范围.
20. (本题满分16)已知函数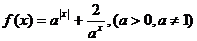
(1)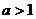 ,解关于
,解关于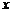 的方程
的方程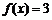 .
.
(2)记函数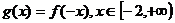 ,若
,若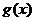 的最值与
的最值与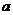 无关,求
无关,求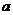 的取值。
的取值。
Ⅱ 必做题部分
19.(本题满分16)在金融危机中,某钢材公司积压了部分圆钢,经清理知共有 根.现将它们堆放在一起.
根.现将它们堆放在一起.
(1)若堆放成纵断面为正三角形(每一层的根数比上一层根数多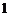 根),并使剩余的圆钢尽可能地少,则剩余了多少根圆钢?
根),并使剩余的圆钢尽可能地少,则剩余了多少根圆钢?
(2)若堆成纵断面为等腰梯形(每一层的根数比上一层根数多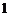 根),且不少于七层,
根),且不少于七层,
(Ⅰ)共有几种不同的方案?
(Ⅱ)已知每根圆钢的直径为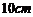 ,为考虑安全隐患,堆放高度不得高于
,为考虑安全隐患,堆放高度不得高于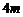 ,则选择哪个方案,最能节省堆放场地?
,则选择哪个方案,最能节省堆放场地?
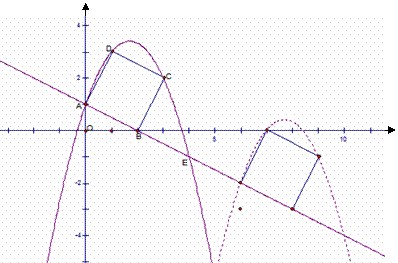
18. (本题满分15)如图,直线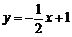 交坐标轴于
交坐标轴于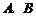 两点,以线段
两点,以线段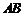 为边向上作正方形
为边向上作正方形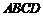 ,过点
,过点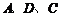 的抛物线与直线的另一个交点为
的抛物线与直线的另一个交点为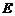 .
.
(1) 求抛物线的解析式.
(2) 若正方形以每秒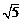 个单位长度沿射线
个单位长度沿射线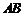 下滑,直至顶点
下滑,直至顶点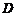 落在
落在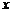 轴上时停止.设正方形落在
轴上时停止.设正方形落在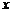 轴下方部分的面积为
轴下方部分的面积为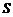 ,求
,求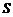 关于滑行时间的函数关系式,并写出自变量的取值范围.
关于滑行时间的函数关系式,并写出自变量的取值范围.
 (3)在(2)的条件下,求有多长时间面积
(3)在(2)的条件下,求有多长时间面积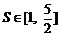 .
.
17. (本题满分15)已知圆 :
: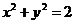 交
交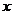 轴于
轴于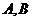 两点,曲线
两点,曲线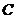 是以
是以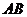 为长轴,离心率为
为长轴,离心率为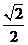 的椭圆,其左焦点为
的椭圆,其左焦点为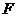 .若
.若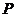 是圆
是圆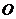 上一点,连结
上一点,连结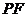 ,过原点
,过原点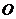 作直线
作直线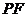 的垂线交椭圆
的垂线交椭圆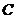 的左准线于点
的左准线于点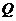 .
.
(Ⅰ)求椭圆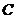 的标准方程;
的标准方程;
(Ⅱ)若点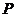 的坐标为(1,1),求证:直线
的坐标为(1,1),求证:直线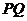 与圆
与圆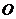 相切;
相切;
(Ⅲ)试探究:当点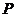 在圆
在圆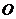 上运动时(不与
上运动时(不与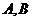 重合),直线
重合),直线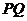 与圆
与圆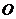 是否保持相切的位置关系?若是,请证明;若不是,请说明理由.
是否保持相切的位置关系?若是,请证明;若不是,请说明理由.
16.
(本题满分14)设向量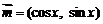 ,
,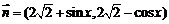 ,若
,若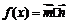
求: (1)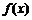 的单调递增区间
的单调递增区间
(2)若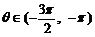 ,且
,且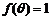 ,求
,求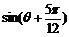 的值.
的值.
15.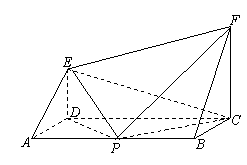 (本题满分14)如图,
(本题满分14)如图,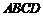 为矩形,
为矩形,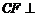 平面
平面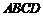 ,
,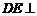 平面
平面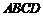 ,
,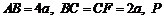 为
为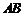 的中点.
的中点.
(1)求证:平面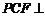 平面
平面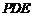 ;(2)求四面体
;(2)求四面体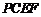 的体积.
的体积.
14.当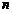 为正整数时,函数
为正整数时,函数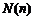 表示
表示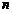 的最大奇因数,如
的最大奇因数,如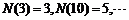 ,
,
设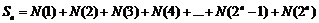 ,则
,则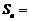 .
.
13. 已知函数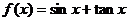 .项数为2009的等差数列
.项数为2009的等差数列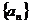 满足
满足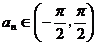 ,且公差
,且公差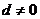 .若
.若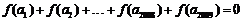 ,则当
,则当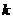 =__________时
=__________时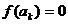 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com