
3. 数列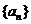 满足递推关系式
满足递推关系式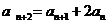 ,
,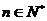 且
且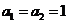 则
则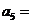 11 .
11 .
2.若不等式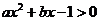 的解集为
的解集为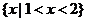 ,则
,则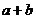 = 1 .
= 1 .
1.已知数列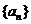 为等差数列,且
为等差数列,且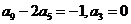 ,则公差
,则公差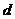 =
= 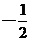 .
.
20.(本题满分16分)设数列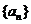 为等差数列首项为
为等差数列首项为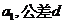 ,数列
,数列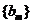 定义如下:对于正整数
定义如下:对于正整数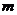 ,
,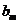 是使得
是使得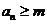 成立的所有
成立的所有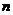 中的最小值.
中的最小值.
(1)若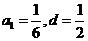 ,求
,求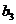 ;
;
(2)若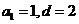 ,求数列
,求数列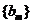 的前
的前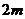 项的和;
项的和;
高三文科数学第2页 (共2页)
19.(本题满分16分)某厂家拟在2010年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)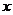 万件与年促销费用
万件与年促销费用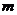 万元
万元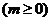 满足
满足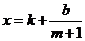 (
(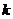 、b为常数),如果不搞促销活动,则该产品的年销售量只能是1万件,如果投入1万元搞促销活动,则该产品的年销售量是2万件.已知2010年生产该产品的固定投入为4万元,每生产1万件该产品需要再投入36万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金,不包括促销费用).
、b为常数),如果不搞促销活动,则该产品的年销售量只能是1万件,如果投入1万元搞促销活动,则该产品的年销售量是2万件.已知2010年生产该产品的固定投入为4万元,每生产1万件该产品需要再投入36万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金,不包括促销费用).
(1)将2010年该产品的利润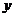 万元表示为年促销费用
万元表示为年促销费用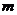 万元的函数;
万元的函数;
(2)该厂家2010年的促销费用投入多少万元时,厂家的利润最大?
18.(本题满分15分)已知关于x的不等式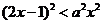 (
(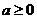 )
)
(1)求此不等式的解集;
(2)若不等式的解集中整数恰好有3个,求正实数a的取值范围.
17.(本题满分15分)已知等比数列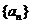 的前
的前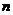 项和为
项和为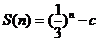 ,数列
,数列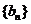
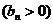 的首项为
的首项为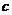 ,且前
,且前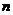 项和
项和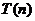 满足
满足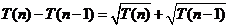 (
(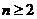 ).
).
(1)设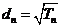 ,求证数列
,求证数列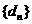 为等差数列,并求其通项公式;
为等差数列,并求其通项公式;
(2)求数列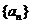 和
和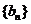 的通项公式;
的通项公式;
(3)若数列{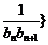 前
前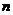 项和为
项和为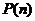 ,问
,问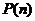 >
>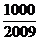 的最小正整数
的最小正整数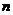 是多少? .
是多少? . 

16.(本题满分14分)数列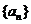 为等差数列,
为等差数列,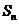 为其前n项和,已知
为其前n项和,已知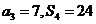
(1)求数列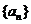 的通项公式和前n项和公式;
的通项公式和前n项和公式;
(2)若p,q为正整数,试比较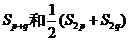 的大小.
的大小.
15.(本题满分14分)等比数列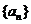 中,已知
中,已知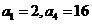 w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m 

(1)求数列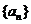 的通项公式;
的通项公式;
(2)若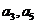 分别为等差数列
分别为等差数列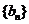 的第3项和第5项,问
的第3项和第5项,问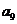 是不是数列
是不是数列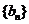 中的项,如果是求出是第几项;如果不是说明理由.
中的项,如果是求出是第几项;如果不是说明理由.
14.设集合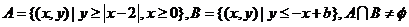 ,若
,若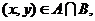 且
且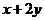 的最大值为11,则
的最大值为11,则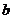 的值是 ▲ .
的值是 ▲ .
高三文科数学第1页 (共2页)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com