3．函数y = e^x + e^−x(e是自然对数的底数)的值域是　 ▲　 ．

2．在△ABC 中，“B=60°”是“A，B，C 成等差数列”的　 ▲　 条件(指充分性和必要性)．

1．已知P = {−1，0，}，Q = { y | y = sin θ，θ∈R}，则P ∩ Q = 　　▲　 ．

20．(本小题满分16分)

已知函数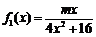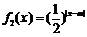，，其中m∈R．

(1)若0<m≤2，试判断函数f (x)=f₁ (x)+f₂ (x)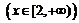的单调性，并证明你的结论；

(2)设函数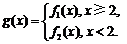 若对任意大于等于2的实数x₁，总存在唯一的小于2的实数x₂，使得g (x₁) = g (x₂) 成立，试确定实数m的取值范围．

19．(本小题满分16分)

某连锁分店销售某种商品，每件商品的成本为4元，并且每件商品需向总店交a元(1≤a≤3)的管理费，预计当每件商品的售价为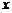元(8≤x≤9)时，一年的销售量为(10－x)²万件．

(1)求该连锁分店一年的利润L(万元)与每件商品的售价x的函数关系式L(x)(销售一件商品获得的利润l＝x－(a+4))；

(2)当每件商品的售价为多少元时，该连锁分店一年的利润L最大，并求出L的最

大值M(a)．

18．(本小题满分15分)

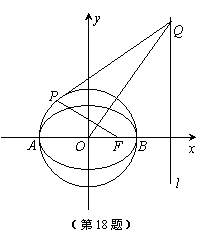如图，已知圆O：x²+y²=2交x轴于A，B两点，点P(－1,1)为圆O上一点．曲线C是以AB为长轴，离心率为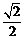的椭圆，点F为其右焦点．过原点O作直线PF的垂线交椭圆C的右准线l于点Q．

(1)求椭圆C的标准方程；

(2)证明：直线PQ与圆O相切．

17．(本小题满分15分)

已知等差数列{a_n}中，首项a₁＝1，公差d为整数，且满足a₁+3＜a₃，a₂+5＞a₄，数列{b_n}满足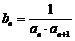，其前n项和为S_n．

(1)求数列{a_n}的通项公式a_n；

(2)若S₂为S₁，S_m(m∈N*)的等比中项，求m的值．

16．(本小题满分14分)

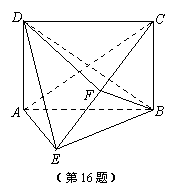如图，四边形ABCD为矩形，平面ABCD⊥平面ABE，BE＝BC，F为CE上的一点，且BF⊥平面ACE．

　 (1)求证：AE⊥BE；

　 (2)求证：AE∥平面BFD．

15．(本小题满分14分)

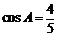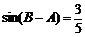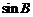在△ABC中，已知，，求的值．

14．若函数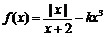有三个不同的零点，则实数k的取值范围为　 　▲　　 ．