
2.经过点(-2,3),且与直线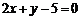 垂直的直线方程为 ▲ .
垂直的直线方程为 ▲ .
1.集合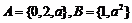 ,若
,若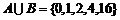 ,则
,则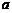 的值为 ▲ .
的值为 ▲ .
20.(本题满分16分)已知二次函数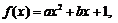 对于任意的实数
对于任意的实数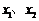
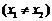 ,
,
都有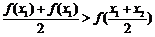 成立,且
成立,且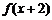 为偶函数.
为偶函数.
(1)求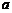 的取值范围;
的取值范围;
(2)求函数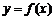 在
在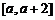 上的值域;
上的值域;
(3)定义区间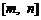 的长度为
的长度为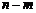 .是否存在常数
.是否存在常数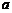 ,使的函数
,使的函数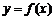 在区间
在区间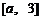 的值域为
的值域为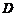 ,且
,且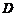 的长度为
的长度为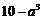 .
.
19.(本题满分16分)已知数列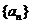 、
、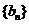 中,对任何正整数
中,对任何正整数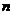 都有:
都有:
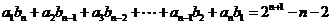 .
.
(1)若数列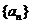 是首项和公差都是1的等差数列,求证:数列
是首项和公差都是1的等差数列,求证:数列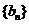 是等比数列;
是等比数列;
(2)若数列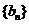 是等比数列,数列
是等比数列,数列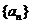 是否是等差数列,若是请求出通项公式,若不是请说明理由;
是否是等差数列,若是请求出通项公式,若不是请说明理由;
18.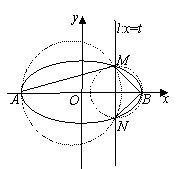 (本题满分15分)已知椭圆
(本题满分15分)已知椭圆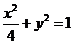 的左、右两个顶点分别为A,B,直线
的左、右两个顶点分别为A,B,直线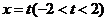 与椭圆相交于M,N两点,经过三点A,M,N的圆与经过三点B,M,N的圆分别记为圆C1与圆C2.
与椭圆相交于M,N两点,经过三点A,M,N的圆与经过三点B,M,N的圆分别记为圆C1与圆C2.
(1)求证:无论t如何变化,圆C1与圆C2的圆心距是定值;
(2)当t变化时,求圆C1与圆C2的面积的和S的最小值.
17.(本题满分15分)已知不等式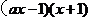 <0 (a∈R).
<0 (a∈R).
(1) 若x=a时不等式成立,求a的取值范围;
(2) 当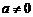 时,解这个关于x的不等式.
时,解这个关于x的不等式.
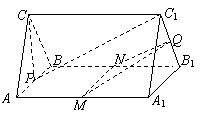 15(本题满分14分)如图已知在三棱柱ABC--A1B1C1中,AA1⊥面ABC,AC=BC,M、N、P、Q分别是AA1、BB1、AB、B1C1的中点.
15(本题满分14分)如图已知在三棱柱ABC--A1B1C1中,AA1⊥面ABC,AC=BC,M、N、P、Q分别是AA1、BB1、AB、B1C1的中点.
(1)求证:面PCC1⊥面MNQ;
(2)求证:PC1∥面MNQ.
16.(本题满分14分)某工厂三个车间共有工人1000名,各车间男、女工人数如下表:
|
|
第一车间 |
第二车间 |
第三车间 |
|
女工 |
173 |
100 |
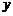 |
|
男工 |
177 |
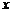 |
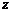 |
已知在全厂工人中随机抽取1名,抽到第二车间男工的概率是0.15.
(1)求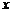 的值;
的值;
(2)现用分层抽样的方法在全厂抽取50名工人,问应在第三车间抽取多少名?
(3)已知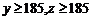 ,求第三车间中女工比男工少的概率.
,求第三车间中女工比男工少的概率.
14.已知函数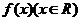 满足
满足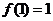 ,且
,且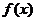 在
在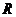 上的导数
上的导数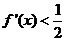 ,则不等式
,则不等式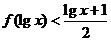 的解集为 ▲ .
的解集为 ▲ .
13.对于数列{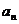 },定义数列{
},定义数列{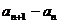 }为数列{
}为数列{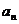 }的“差数列”,若
}的“差数列”,若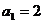 ,{
,{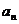 }的“差数列”的通项公式为
}的“差数列”的通项公式为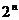 ,则数列{
,则数列{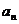 }的前
}的前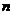 项和
项和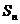 = ▲ .
= ▲ .
12.给出下列关于互不相同的直线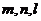 和平面
和平面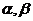 的四个命题:
的四个命题:
(1)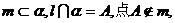 则
则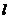 与m不共面;
与m不共面;
(2)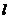 、m是异面直线,
、m是异面直线,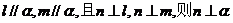 ;
;
(3)若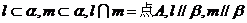 ,则
,则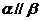 ;
;
(4)若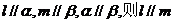
其中真命题是 ▲ .(填序号)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com