3.　　　　 引导学生应用集合与对应的语言描述各个实例中两个变量间的依赖关系；

1.　　　　 复习初中所学函数的概念，强调函数的模型化思想；

2、 提高内容：

(1)　　　 已知X={x|x²+px+q=0，p²-4q>0},A={1,3,5,7,9},B={1,4,7,10}，且

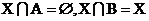，试求p、q；

(2)　　　 集合A={x|x²+px-2=0},B={x|x²-x+q=0},若A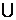B={-2，0，1}，求p、q；

(3)　　　 A={2，3，a²+4a+2}，B={0，7，a²+4a-2，2-a}，且A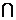B ={3，7}，求B

1、 书面作业：P₁₃习题1.1，第6-12题

6.　　　　 课堂练习 (1)设A={奇数}、B={偶数}，则A∩Z=A，B∩Z=B，A∩B=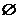 (2)设A={奇数}、B={偶数}，则A∪Z=Z，B∪Z=Z，A∪B=Z

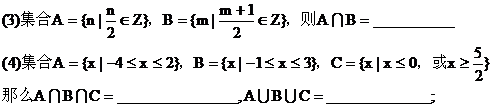
5.　　　　 集合基本运算的一些结论：

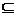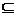A∩BA，A∩BB，A∩A=A，A∩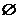=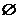,A∩B=B∩A

A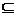A∪B，B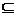A∪B，A∪A=A，A∪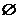=A,A∪B=B∪A

(C_UA)∪A=U，(C_UA)∩A=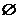

若A∩B=A，则A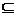B，反之也成立

若A∪B=B，则A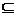B，反之也成立

若x∈(A∩B)，则x∈A且x∈B

若x∈(A∪B)，则x∈A，或x∈B

4.　　　　 求集合的并、交、补是集合间的基本运算，运算结果仍然还是集合，区分交集与并集的关键是“且”与“或”，在处理有关交集与并集的问题时，常常从这两个字眼出发去揭示、挖掘题设条件，结合Venn图或数轴进而用集合语言表达，增强数形结合的思想方法。

3.　　　　 补集

全集：一般地，如果一个集合含有我们所研究问题中所涉及的所有元素，那么就称这个集合为全集(Universe)，通常记作U。

补集：对于全集U的一个子集A，由全集U中所有不属于集合A的所有元素组成的集合称为集合A相对于全集U的补集(complementary set),简称为集合A的补集，

记作：C_UA

即：C_UA={x|x∈U且x∈A}

补集的Venn图表示

说明：补集的概念必须要有全集的限制

例题(P₁₂例8、例9)

2.　　　　 交集

一般地，由属于集合A且属于集合B的元素所组成的集合，叫做集合A与B的交集(intersection)。

记作：A∩B　　　　　　　　　　　 读作：“A交B”

　　　 即：　 A∩B={x|∈A，且x∈B}

交集的Venn图表示

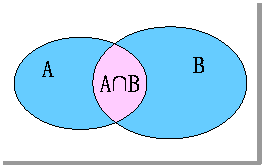
说明：两个集合求交集，结果还是一个集合，是由集合A与B的公共元素组成的集合。

例题(P_9-10例6、例7)

拓展：求下列各图中集合A与B的并集与交集

说明：当两个集合没有公共元素时，两个集合的交集是空集，而不能说两个集合没有交集