4．　　 某影院的某场电影的每一张电影票有唯一确定的座位与它对应；

3．　　 对于任意一个三角形，都有唯一确定的面积和它对应；

2．　　 对于坐标平面内任何一个点A，都有唯一的有序实数对(x,y)和它对应；

复习初中已经遇到过的对应：

1．　　 对于任何一个实数a，数轴上都有唯一的点P和它对应；

课本P₂₈ 习题1．2(A组) 第1-7题 (B组)第1题

从具体实例引入了函数的的概念，用集合与对应的语言描述了函数的定义及其相关概念，介绍了求函数定义域和判断同一函数的典型题目，引入了区间的概念来表示集合。

(三)课堂练习

求下列函数的定义域

(1)

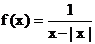
(2)

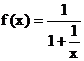
(3)

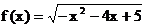
(4)

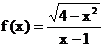
(5)

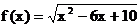
(6)

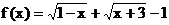
(二)典型例题

1．求函数定义域

　　　 课本P₂₀例1

　　　 解：(略)

　　　 说明：

1 函数的定义域通常由问题的实际背景确定，如果课前三个实例；

2 如果只给出解析式y=f(x)，而没有指明它的定义域，则函数的定义域即是指能使这个式子有意义的实数的集合；

3 函数的定义域、值域要写成集合或区间的形式．

巩固练习：课本P₂₂第1题

2．判断两个函数是否为同一函数

课本P₂₁例2

解：(略)

　　　 说明：

1 构成函数三个要素是定义域、对应关系和值域．由于值域是由定义域和对应关系决定的，所以，如果两个函数的定义域和对应关系完全一致，即称这两个函数相等(或为同一函数)

2 两个函数相等当且仅当它们的定义域和对应关系完全一致，而与表示自变量和函数值的字母无关。

巩固练习：

1 课本P₂₂第2题

2 判断下列函数f(x)与g(x)是否表示同一个函数，说明理由？

(1)f ( x ) = (x －1) ⁰；g ( x ) = 1

(2)f ( x ) = x； g ( x ) =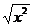

(3)f ( x ) = x ²；f ( x ) = (x + 1) ²

(4)f ( x ) = | x | ；g ( x ) =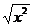

(一)函数的有关概念

1．函数的概念：

设A、B是非空的数集，如果按照某个确定的对应关系f，使对于集合A中的任意一个数x，在集合B中都有唯一确定的数f(x)和它对应，那么就称f：A→B为从集合A到集合B的一个函数(function)．

记作：　　　　　　　　　 y=f(x)，x∈A．

其中，x叫做自变量，x的取值范围A叫做函数的定义域(domain)；与x的值相对应的y值叫做函数值，函数值的集合{f(x)| x∈A }叫做函数的值域(range)．

注意：

1 “y=f(x)”是函数符号，可以用任意的字母表示，如“y=g(x)”；

2 函数符号“y=f(x)”中的f(x)表示与x对应的函数值，一个数，而不是f乘x．

2．　 构成函数的三要素：

定义域、对应关系和值域

3．区间的概念

　　　 (1)区间的分类：开区间、闭区间、半开半闭区间；

　　　 (2)无穷区间；

　　　 (3)区间的数轴表示．

4．一次函数、二次函数、反比例函数的定义域和值域讨论

　　　 (由学生完成，师生共同分析讲评)

4.　　　　 根据初中所学函数的概念，判断各个实例中的两个变量间的关系是否是函数关系．