2.若是纯虚数，则实数的值是　 ▲ 　。

1.已知集合，则　 ▲　 。

20．(本题满分16分)

已知点(1，)是函数且)的图象上一点，等比数列的前项和为,数列的首项为，且前项和满足－=+().

(1)求数列和的通项公式；

(2)若数列{前项和为，问>的最小正整数是多少? .　 　

19．(本题满分16分)

设，

(1)令，讨论在(0.+∞)内的单调性并求极值；

(2)求证：当时，恒有。

18．(本题满分16分)

已知圆C：x²+y²+2x-4y+3=0；

(1)若圆C的切线在x轴和y轴上的截距相等，求此切线的方程。

(2)从圆C外一点P(x₁,y₁)向该圆引一条切线，切点为M，O为坐标原点，且有|PM|=|PO|，求使得|PM|取得最小值的点P的坐标。

17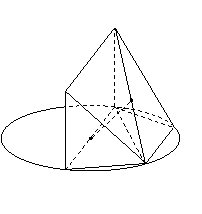．(本题满分14分)

如图，为圆的直径，点、在圆上，且，矩形所在的平面和圆所在的平面互相垂直，且，.

(Ⅰ)求证：平面；

(Ⅱ)设的中点为，求证：平面；

(Ⅲ)求四棱锥的体积．

16. (本题满分14分)

已知集合，

(1)当时，求；

(2)若，求实数的取值范围.

15．(本题满分14分)

在中，为锐角，角所对的边分别为，且

(I)求的值；

(II)若，求的值。

14．若曲线不存在垂直于轴的切线，则实数取值范围是　　 ★　　 ．

13．函数的图象关于轴对称，定义域为，则 的值域为　 ★　 .