
1.设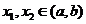 且
且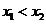 ,若恒有
,则
,若恒有
,则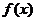 在
在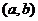 上 。
上 。
7.奇偶性运算:奇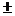 奇= 偶
奇= 偶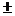 偶= 奇
偶= 奇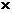 偶= 奇
偶= 奇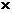 奇= 偶
奇= 偶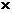 偶=
偶=
6.常见函数的奇偶性: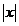 为 ;
为 ;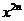 为 (
为 (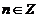 );
);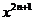 为
(
为
(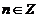 )
)
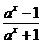 为
;
为
;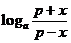 为
(
为
(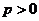 )。
)。
5.若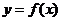 为奇函数且
为奇函数且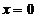 有意义,则有
有意义,则有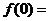 。
。
4.若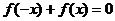 ,则函数
,则函数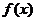 为
。
为
。
若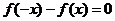 ,则函数
,则函数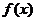 为
。
为
。
3.设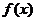 为定义在A上的奇函数,是指 对一切
为定义在A上的奇函数,是指 对一切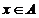 恒成立,特别地,取定值
恒成立,特别地,取定值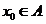 有等式
。
有等式
。
2.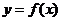 具有奇偶性的一个必要条件式定义域关于
对称。
具有奇偶性的一个必要条件式定义域关于
对称。
1.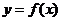 满足
则为奇函数,其图像关于
中心对称;
满足
则为奇函数,其图像关于
中心对称;
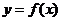 满足
则为偶函数,其图像关于
对称。
满足
则为偶函数,其图像关于
对称。
8.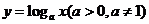 当
当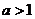 时,函数在
上递 。
时,函数在
上递 。
当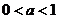 时,函数在
上递 。
时,函数在
上递 。
7.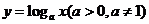 定义域为
;值域为
。
定义域为
;值域为
。
若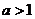 ,
,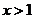 则
则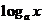 0;若
0;若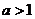 ,
,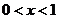 则
则 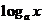 0
0
若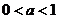 ,
,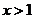 则
则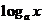 0;若
0;若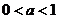 ,
,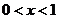 则
则 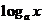 0
0
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com