
第一节:单项填空(共15小题,每小题1分,满分15分)
从A、B、C、D四个选项中,选出可以填入空白处的最佳选项,并在答题卡上将该项涂黑。
21. -Thank you for having bought me a ticket for the World Expo in Shanghai!
- ________.
A. Come on B. All right C. No problem D. With pleasure
22.[解析](Ⅰ)∵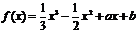 ,∴
,∴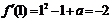 ,
,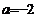
∴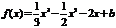 ,∴
,∴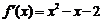 .令
.令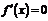 , 即
, 即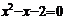 ,
,
解得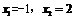 (3分),当
(3分),当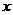 变化时,
变化时,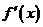 ,
,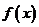 变化情况如下表:
变化情况如下表:
 ……(6分)
……(6分)
∵函数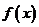 的图象与
的图象与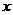 轴有三个交点,∴
轴有三个交点,∴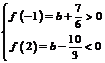 ,∴
,∴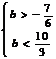 ,
,
∴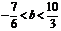 .∴
.∴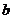 的取值范围为
的取值范围为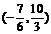 ………………………………………(8分)
………………………………………(8分)
(Ⅱ)由(Ⅰ)知,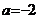 ,函数
,函数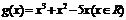 .∴
.∴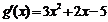 ,令
,令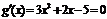 得,
得,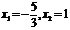 ,列表如下:
,列表如下:

由上表知,函数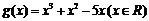 的单调增区间为
的单调增区间为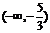 和
和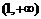 ,单调减区间为
,单调减区间为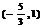 .………(12分)
.………(12分)
21.[解析](Ⅰ)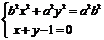 消去
消去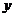 得:
得: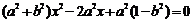
令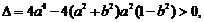 得
得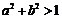 .……………………(2分)
.……………………(2分)
设点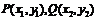 ,则
,则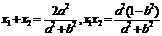 ,由
,由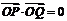 ,得
,得
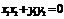 ,即
,即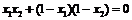 ,化简得
,化简得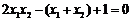 ,
,
则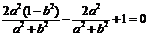 ,即
,即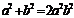 ,故
,故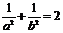 .…………………(6分)
.…………………(6分)
(Ⅱ)∵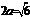 ,∴
,∴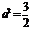 ,由(Ⅰ)知
,由(Ⅰ)知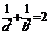 ,∴
,∴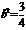 ,∴椭圆的标准方程为
,∴椭圆的标准方程为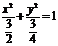 .
.
∵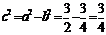 ,∴
,∴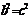 ,即
,即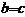 .∴焦点在以短轴为直径的圆上。(8分)
.∴焦点在以短轴为直径的圆上。(8分)
(Ⅲ)由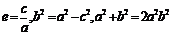 ,化简得:
,化简得: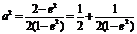 (10分)
(10分)
由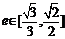 得
得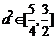 ,即
,即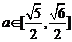 ,故椭圆的长轴长的取值范围是
,故椭圆的长轴长的取值范围是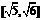 .(12分)
.(12分)
20.[解析](Ⅰ)∵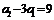 ,
,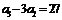 ,∴
,∴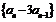 是以3为公比的等比数列.
是以3为公比的等比数列.
∴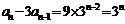 .等式两边同除以
.等式两边同除以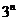 ,得
,得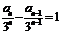 ,∴
,∴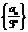 是等差数列.(4分)
是等差数列.(4分)
(Ⅱ)根据(Ⅰ)可知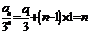 ,∴
,∴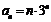
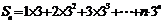 ①
①
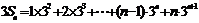 ②,①-②得:
②,①-②得: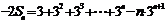
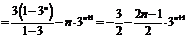 ,∴
,∴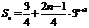 .………………………(12分)
.………………………(12分)
19.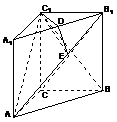 [解析]解法一:(Ⅰ)在直三棱柱ABC-A1B1C1中,∵CC1⊥
[解析]解法一:(Ⅰ)在直三棱柱ABC-A1B1C1中,∵CC1⊥
平面ABC,∴CC1⊥AC,∵BC=CC1,∴BCC1B1为正方形.∴BC1
⊥B1C(2分),又∵∠ACB=90°,∴AC⊥BC∴AC⊥平面BCC1B1,
∵B1C为AB1在平面BCC1B1内的射影,BC1⊥B1C,∴AB1⊥BC1,
(4分)
(Ⅱ)∵BC//B1C,∴BC//平面AB1C1,∴点B到平面AB1C1
的距离等于点C到平面AB1C1的距离(5分)连结A1C交AC1
于H,∵ACC1A1是正方形,∴CH⊥AC1.∵B1C1⊥A1C1,B1C1
⊥CC1,∴B1C1⊥A1C1,B1C1⊥CC1,∴B1C1⊥平面ACC1A1.
∴B1C1⊥CH.∴CH⊥平面AB1C1,∴CH的长度为点C到平面AB1C1的距离.
∵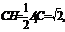 ∴点B到平面AB1C1的距离等于
∴点B到平面AB1C1的距离等于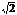 (8分)
(8分)
(Ⅲ)取A1B1的中点D,连接C1D,∵△A1B1C1是等腰三角形,所以C1D⊥A1B1,又∵直三棱柱ABC-A1B1C1中,侧面A1B1BA⊥底面A1B1C1,∴C1D⊥侧面A1B1BA.作DE⊥AB1于E,;连C1E,则DE为C1E的平面A1B1BA内的射影,∴C1E⊥AB1
∴∠C1ED为二面角C1-AB1-A1的平面角.……………………(10分)
由已知C1D=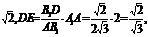 ∴
∴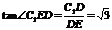 ,∴
,∴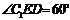
即二面角C1-AB1-A1的大小为60°…………………………(12分)
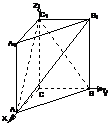 解法二:如图建立空间直角坐标系,依题意A(2,0,0),
解法二:如图建立空间直角坐标系,依题意A(2,0,0),
B(0,2,0),A1(2,0,2),B1(0,2,2),C1(0,0,2).(2分)
(Ⅰ)证明: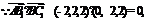
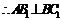
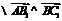 …(4分)
…(4分)
(Ⅱ)设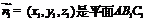 的法向量,由
的法向量,由
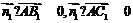 得
得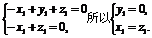 令
令
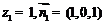 (6分),
(6分),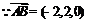 ,∴点B到平面
,∴点B到平面
AB1C1的距离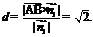 ……………………(8分)
……………………(8分)
(Ⅲ)解设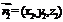 是平面A1AB1的法向量,由
是平面A1AB1的法向量,由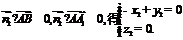
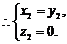 令
令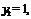 则
则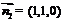 (10分),
(10分),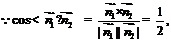
∴二面角C1-AB-A1的大小为60°.…………………………(12分)
18.[解析]基本事件的总数为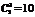 ,事件“
,事件“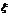 ≤
≤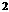 ”,即“
”,即“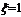 ”所包含的基本事件有6个:“123”,“124”,“125”,“134”,“135”,“145”; “
”所包含的基本事件有6个:“123”,“124”,“125”,“134”,“135”,“145”; “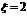 ”所包含的基本事
”所包含的基本事
件有3个:“234”,“235”,“245”,∴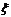 ≤
≤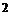 的概率为
的概率为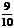 ;(6分),事件“
;(6分),事件“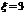 ”所包含的基本事件有1个:“345”,∴
”所包含的基本事件有1个:“345”,∴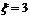 的概率为
的概率为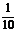 .……(12分)
.……(12分)
17.[解析](Ⅰ)由已知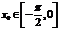 ,且
,且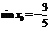 ,可得
,可得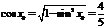 ,
,
∴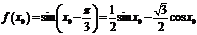 ,
,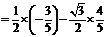
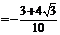 ; …(5分)
; …(5分)
(Ⅱ)将函数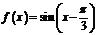 的图象向左平移
的图象向左平移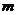 个单位,得
个单位,得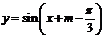 图象关于
图象关于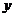 轴对称,∴
轴对称,∴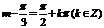 (7分),∴
(7分),∴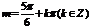 ,又∵
,又∵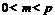
∴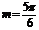 ,∴
,∴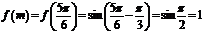 .………………………(10分)
.………………………(10分)
16.[答案]25[解析]不等式表示的平面区域如图所示阴
影部分,当直线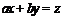 (a>0,b>0)过直线x-y+2=0与直
(a>0,b>0)过直线x-y+2=0与直
线3x-y-6=0的交点(4,6)时,目标函数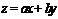 (a>0,b>0)取得最大12,∴4a+6b=12,即2a+3b=6.
(a>0,b>0)取得最大12,∴4a+6b=12,即2a+3b=6.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com