22.(1)证明：由条件知M点的坐标为，其中，

，　　 　　　　　　　　…… 3分

，即成等比数列．　　　 　　　　　　　　…… 4分

(2)由条件知， 　　　　　　　…… 6分

椭圆方程为　　　　　　 　　　　…… 8分

(3)[文科]设点A、B，

当轴时，A、B，所以．　　　 …… 9分

设直线的方程为，

代入椭圆方程得．…………… 11分

所以…………………………………………… 13分

由得

代入得，解得．

所以直线的方程为．　　　　　　 …… 16分

[理科]设点P(x,y)，A、B，由 ，得

当轴时，A、B，

此时P不在椭圆上．　　　 　　　　　　　　　　…… 9分

设直线的方程为，代入椭圆方程得

．　　　　　　　　 …… 11分

所以 … 13分

把点P(x,y)代入椭圆方程得，解得，

所以直线的方程为．　　　　　　 …… 16分

22. (2010年4月上海杨浦、静安、青浦、宝山四区联合高考模拟)(本题满分16分)本题共有3个小题，第1小题满分4分，第2小题满分4分，第3小题满分8分．

已知为椭圆,的左右焦点，是坐标原点，过作垂直于轴的直线交椭圆于，设 .

(1)证明： 成等比数列；

(2)若的坐标为，求椭圆的方程；

(3)[文科]在(2)的椭圆中，过的直线与椭圆交于、两点，若，求直线的方程．

[理科]在(2)的椭圆中，过的直线与椭圆交于、两点，若椭圆上存在点，使得 ，求直线的方程．

19．(1)方法一：如图，以线段的中点为原点，

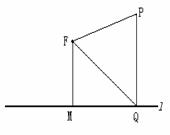　 以线段所在的直线为轴建立直角坐标系．

则，．　　　 　　　……………………………2分

设动点的坐标为，则动点的坐标为

，， 　　…………2分

由，得，…2分

方法二：由得，．…………………………2分

所以，动点的轨迹是抛物线，以线段的中点

为原点，以线段所在的直线为轴建立直角坐标系，可得轨迹的方程为：．…………………………………………………………4分

(2)方法一：如图，设直线的方程为，，，……1分

则. ……………………………………………………………………………1分

联立方程组消去得，

，，故 …………………………………………1分

　 ……………………………………………………………………………1分

由，得，

，，……………………………………………………2分

整理得，，，

.…………………4分

方法二：由已知，，得.　　 …………………2分

于是，，　　 ① …………………………………………………3分

如图，过、两点分别作准线的垂线，垂足分别为、，

则有　　 ② …………………………………………………3分

由①，②得.…………………………………………………………………2分

19．(上海市闸北区2010年4月高三第二次模拟理科)(满分16分)本题有2小题，第1小题6分，第2小题10分．

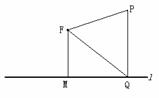　 如图，平面上定点到定直线的距离，为该平面上的动点，过作直线的垂线，垂足为，且．

(1)试建立适当的平面直角坐标系，求动点的轨迹的方程；

(2)过点的直线交轨迹于、两点，交直线于点，

已知，，求证：为定值．

22．解：(1)，-----------------------------------------------------2分

代入----------------------------------　 4分

当时，点 在圆上-------------------------------------------5分

(2)在椭圆上，即

可设------------------------------------------------------------------------7分

又，于是

(令)

点在双曲线上--------------------------------------------------------------------10分

(3)圆的方程为

设由

　----------------------------------------------------------------------------------------------12分

又

，------------14分

又原点到直线距离 ，即原点到直线的距离恒为

直线恒与圆相切。---------------------------------------------------------16分

22．(上海市徐汇区2010年4月高三第二次模拟理科)(本题满分16分；第(1)小题5分，第(2)小题5分，第(3)小题6分)

设、为坐标平面上的点，直线(为坐标原点)与抛物线交于点(异于).

(1)　　　 若对任意，点在抛物线上，试问当为何值时，点在某一圆上，并求出该圆方程；

(2)　　　 若点在椭圆上，试问：点能否在某一双曲线上，若能，求出该双曲线方程，若不能，说明理由；

(3)　　　 对(1)中点所在圆方程，设、是圆上两点，且满足，试问：是否存在一个定圆，使直线恒与圆相切.

21．(上海市松江区2010年4月高考模拟理科)(本题16分，其中第(1)小题8分，第(2)小题8分)

已知椭圆的方程为，长轴是短轴的2倍，且椭圆过点，斜率为的直线过点，为直线的一个法向量，坐标平面上的点满足条件．

(1)写出椭圆方程，并求点到直线的距离；

(2)若椭圆上恰好存在3个这样的点，求的值．

解：(1)由题意得　 解得　 …………3分

∴椭圆方程为：　　　　　　　　　　　　 …………4分

直线的方程为，其一个法向量，设点B的坐标为，由及　 得　 　…………6分

∴到直线的距离为　 …………8分

(2)由(1)知，点B是椭圆上到直线的距离为1的点，即与直线的距离为1的二条平行线与椭圆恰好有三个交点。　　　　　　　　　

设与直线平行的直线方程为

由得，即

………①…………10分

当时，………②

又由两平行线间的距离为1，可得………③

把②代入③得，即，

即，或　　　　　　　　　　　　　　　　　　　　 …………12分

当时，代入②得，代回③得或　　

当，时，由①知

此时两平行线和与椭圆只有一个交点，不合题意；…………14分

当时，代入②得，代回③得或

当，时，由①知

此时两平行线和，与椭圆有三个交点，

∴　　　　　　　　　　 　　　　…………16分

23、解：(1)　 　　　　

　 。　　　　　　　 ……………………………………4分

(2)　 　　由得

由 得　　 　

……………………………………6分

……………………………………8分

设，则

　　　　　　 ……………………………………10分

。　　　　　 ……………………………………12分

(3),　 ,

　　　　　　　　　 ……………………………………14分

因为

　……………………………………16分

　　 即　

　　 ，　 　　　

……………………………………18分