21．(本题满分14分)

已知函数

　 (I)(i)求函数的图象的交点的坐标；

　　　 (ii)设函数的图象在交点处的切线分别为是否存在这样的实数，使得？若存在，请求出的值和相应交点的坐标；若不存在，请说明理由.

　 (II) 求函数在上最小值.

20．(本题满分14分)

设分别为椭圆的左、右顶点，椭圆长半轴的长等于焦距，且.

(1)　 求椭圆的方程；

(2)　 设为直线上不同于点的任意一点，

若直线分别与椭圆相交于异于的点，

证明点在以为直径的圆内.

19． (本题满分14分)

已知数列是以首项为，公比的等比数列，设，

数列.

(1)求证：是等差数列；

(2)求数列的前项和；

(3)若一切正整数恒成立，求实数的取值范围.

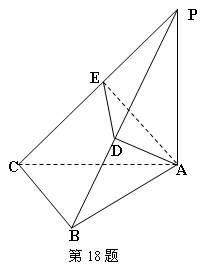
18．(本题满分14分)

如图，平面， ．垂直于于，

垂直于于．，．

(1)求证：平面；

　(2)求与平面所成的角；

17. (本题满分12分)

第19届南非世界杯的主办城市开普敦有甲乙两个相邻的观光景点，某日甲景点内有2个美国旅游团和2个日本旅游团，乙景点内有2个美国旅游团和3个日本旅游团 . 现从甲景点中的4个旅游团选出其中一个旅游团，与从乙景点中的5个旅游团中选出的其中一个旅游团进行互换.

　　　 (1)求互换后甲景点恰有2个美国旅游团的概率；

　　　 (2)求互换后甲景点内美国旅游团数的期望.

16．(本题满分12分)

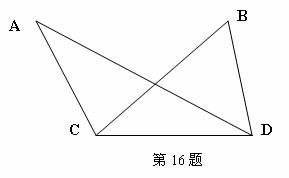2010年上海世博会上展馆与展馆位于观光路的同侧,在观光路上相距千米的两点分别测得，(在同一平面内)，求展馆之间的距离.

(二)选做题(14 ~ 15题，考生只能从中选做一题.若两题都做，只计算14题的得分)

14. 在极坐标中，圆的圆心到直线

的距离为　　　　　　　　　 .

15．如右图，直线与圆相切于点，割线经过圆心，

弦⊥于点，，，则　　　　　　 ..

(一)必做题(9-13题)

9．的展开式中，只有第六项的系数最大，则的系数是　　　　　　 .

10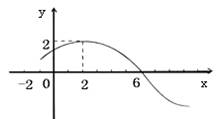．已知函数的图象如图所示，则函数的解析式 　　　　　　　.

11．椭圆的两个焦点在圆上，则此椭圆的离心率　　　　　　 　.

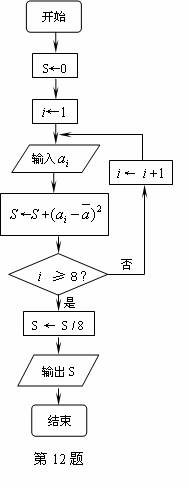
12. 对一个作直线运动的质点的运动过程观测了8次,

得到如下表所示的数据.

观测次数	1	2	3	4	5	6	7	8
观测数据	40	48	46	43	44	43	47	41

在上述统计数据的分析中,其中一部分的计算见右图所示

的算法流程图(其中是这8个数据的平均数),

则输出的S的值是　　　　　 .

13.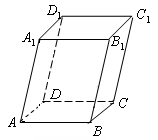 定义向量运算“”：的结果为一个向量，其模为，且与向量均垂直．则右图平行六面体的体积用表示为　　　　　　　　　 ．(用运算符号“”及数量积“”表示)

8. 定义在上的函数, 若关于的方程有个不同实数解、、，且，则下列结论错误的是(　　　 )

．　　　 . 　　　　. 　　　.

7．在第16届广州亚运会中，某国家队从名运动员中选名运动员参加米接力赛，

且这人中甲、乙两人不跑第一棒，则不同的选择方案共有(　　　 )

　　 　．种 　　　　 ．种　 　　　 ．种　　　 　　 ．种