8.关于地球同步卫星，它们具有相同的

A．质量　　　 B．高度　　 C．向心加速度　　　 D．周期

5.水能是可再生能源，可持续地利用它来发电，为人类提供“清洁”的能源.一水力发电站，水流的落差为h=20m,水流冲击水轮机发电时，水流动能的20%将转化为电能，若发电机的功率是200kw,g取10m/s²,则每分钟流下的水量是(水流初始动能不计)

A．1.5×10⁶ kg　　 B．3×10⁵ kg　　　 C．6×10⁴ kg　　　 D．6×10⁵ kg 6.某消防队员从一平台上跳下，下落2m后双脚触地，接着他用双腿弯屈的方法缓冲，使自身重心又下降了0.5m．在着地过程中地面对他双脚的平均作用力估计为 　　 A．自身所受重力的2倍B．自身所受重力的4倍 　　 C．自身所受重力的5倍D．自身所受重力的10倍 7.如图，一很长的、不可伸长的柔软轻绳跨过光滑定滑轮，绳两端各系一小球a和b．a球质量为m，静置于地面；b球质量为3m， 用手托住，高度为h，此时轻绳刚好拉紧．从静止开始释放b后，a可能达到的最大高度为

A．h　　　 B．1.5h　　 C．2h　　 D．2.5h

4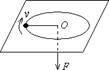．如右图所示，质量为m的物体用细绳经过光滑小孔牵引在光滑水平面 上做匀速圆周运动，拉力为某个值F时，转动半径为R，当拉力逐渐减小 到F/4时，物体仍做匀速圆周运动，半径为2R，则外力对物体所做的功 大小是

A．　　　　 B．　　　　 C．　　 　　D．零

3.如图所示，水平天花板下用长度相同的绝缘细线悬挂起来的两个相同的带电小球A、B，左边放一个带正电的固定球时，两悬线都保持竖直方向．下面说法中正确的是

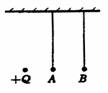A．A球带正电，B球带负电，并且A球带电荷量较大

B．A球带负电，B球带正电，并且A球带电荷量较大

　C．A球带负电，B球带正电，并且A球带电荷量较小

D．A球带正电，B球带负电，并且A球带电荷量较小

2. 两个分别带有电荷量和+的相同金属小球(均可视为点电荷)，固定在相距为的两处，它们间库仑力的大小为。两小球相互接触后将其固定距离变为，则两球间库仑力的大小为

　　 A．　　　　　 B．　　　　　 C．　　　　　 D．

1.宇宙飞船正在离地面高的轨道上做匀速圆周运动，飞船内一弹簧秤下悬挂一质量为m的重物，g为地面处重力加速度，则弹簧秤的读数为

A．mg　 B．mg C．mg　　 D．0

22、(本小题满分14分)

解(1)∵函数图象关于原点对称，∴对任意实数，　 1分

，即恒成立，

，　

．　 3分

∵ x = 1时，取极小值－，

∴ 3a + c = 0且a + c = －，

解得a = ，c = －1．　 5分

　 (2)当时，图象上不存在这样的两点使结论成立．　 6分

假设图象上存在两点、，使得过此两点处的切线互相垂直，

则由知两点处的切线斜率分别为，

且…………(*)　 8分

∵x₁、，，　

此与(*)相矛盾，故假设不成立．　 9分

(3)证明：f^/(x) = x²－1，令f^/(x) = 0，得x = ±1，

∵ x Î (－¥,－1)或x Î (1, + ¥)时，f^/(x)>0；x Î (－1,1)时，f^/(x)<0，　 10分

上是减函数，且，　 11分

∴在[－1，1]上，有| f(x) |≤成立，　　 12分

于是当x­₁，x₂ Î [－1,1]时，．　 14分

21、(本小题满分12分)

解：(1) 由a₂ = 6，= 1，= 2，= 3，　 1分

解得a­₁ = 1，a₃ = 15，a₄ = 28．　 3分

(2) 由此猜想a_n = n (2n－1) ．　 4分

下面用数学归纳法加以证明：

①　　 当n = 1时，a₁ = 1×(2×1－1) = 1，结论正确；

当n = 2时，a₁ = 2×(2×2－1) = 6，结论正确．　 5分

②　　 假设n = k (k≥2)时结论正确，即a_k = k(2k－1) ．

则当n = k + 1时，∵　 = k，

∴　　 (k－1)a_{k + 1} = (k + 1)a _k－(k + 1) = (k + 1)k(2k－1)－(k + 1)

= (k + 1)(2k²－k－1) = (k + 1)(2k + 1)(k－1)，

∵　　 k－1 ≠ 0，∴　　 a_{k + 1} = (k + 1)[2(k + 1)－1]，

即当n = k + 1时，结论正确．　　　　　　　　　　 7分

由①②可知，{a_n} 的通项公式是a_n = n (2n－1) ．　 8分

(3) ∵　　 　= 　= ( －)　 10分

∴　　 (+ + ┄ + ) = (1－) = ．　 12分

20、(本小题满分12分)

解：(1)设切去正方形边长为x，则焊接成的长方体的底面边长为4－2x，高为x，　 1分

所以V=(4－2x)²·x = 4(x³－4x² + 4x)　 (0<x<2) ．　　 3分

∴　　 V^/ = 4(3x²－8x + 4)，　　 4分

令V^/ = 0，即4(3x²－8x + 4) = 0，解得x₁ = ，x₂ = 2 (舍去) ．　 6分

又当x<时，V^/>0；当<x<2时，V^/<0．　　 7分

∴　　 当x = 时，V取得最大值V₁ = ．　 8分

(2)重新设计方案如下：

如图①，在正方形的两个角处各切下一个边长为1的小正方形；如图②，将切下的小正方形焊在未切口的正方形一边的中间；如图③，将图②焊成长方体容器.新焊长方体容器底面是一个长方形，长为3，宽为2，此长方体容积V₂ = 3×2×1 = 6，显然V₂>V₁．

故第二种方案符合要求．

　　　　　 图①　　　　　　　　　　　 图②　　　　　　　　　 　　　图③

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 12分

19、(本小题满分12分)

解：设z = a + bi (a,b Î R)，则z² = (a²－b²) + 2abi ，　 2分

　　 ∴　　 (a²－b²) + 2abi = 3 + 4i 　Û ，　 3分

　　 解得 或 ，　　 5分

　　 即z = 2 + i或z = －2－i ．　　　 6分

　　 又z³－6z + = 　= － ，　　 8分

　　 当z = 2 + i时，z³－6z + 　= －　= －+ i ；　 10分

　　 当z = －2 － i时，z³－6z + 　= －　= － i ．　 12分