7. 已知

　　 的单调区间；

　　 (2)若

　　 讲解: (1) 对 已 知 函 数 进 行 降 次 分 项 变 形　 , 得 ,

　　 (2)首先证明任意

事实上,

　　 而

　　 　.

6.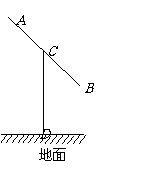某建筑的金属支架如图所示，根据要求至少长2.8m，为的中点，到的距离比的长小0.5m，，已知建筑支架的材料每米的价格一定，问怎样设计的长，可使建造这个支架的成本最低？

解析：设

　　　 连结BD.

　　　 则在中，

　　　 设

　　　 则

　　　 等号成立时

　　　 答：当时，建造这个支架的成本最低.

5. 某公司租地建仓库，每月土地占用费y₁与车库到车站的距离成反比，而每月库存货物的运费y₂与到车站的距离成正比，如果在距车站10公里处建仓库，这两项费用y₁和y₂分别为2万元和8万元，那么要使这两项费用之和最小，仓库应建在离车站多少公里处?

解析：由已知y₁=；y₂=0.8x(x为仓库与车站距离)费用之和y=y₁+y₂=0.8x+ ≥2=8当且仅当0.8x=即x=5时“=”成立

答：5公里处

综合拔高训练

4. 半径为4的球面上有A、B、C、D四点，且AB，AC，AD两两互相垂直，则、、面积之和的最大值为　　　　　　　　　　　　 (　 )C

　　 A．8　　　　　　　 B．16　　　　　　 C．32　　　　　　 D．64

解析：由AB，AC，AD两两互相垂直，将之补成长方体知AB²+AC²+AD²=(2R)²=64．

　　 ≤=．

等号当且仅当取得，所以的最大值为32 ，选C．

3. (广东省梅州、揭阳两市四校2008届高三第三次联考)设x，y均为正实数，且，则xy的最小值为 　　　　

解析：由可化为xy =8+x+y,x，y均为正实数

　xy =8+x+y(当且仅当x=y等号成立)即xy-2-8

可解得,即xy16故xy的最小值为16。

2. 设实数x,y满足，则x+y的取值范围是____．

解析：．答案为(-∞,-1]∪[1, +∞)_

1. 设x≠0，则函数在x=____时，y有最小值____．

解：．答案为： __±1__；3

7. (广东省潮州金中08-09学年高三上学期期中考试)某种汽车的购车费用是10万元，每年使用的保险费、养路费、汽油费约为万元，年维修费用第一年是万元，以后逐年递增万元。问这种汽车使用多少年时，它的年平均费用最小？最小值是多少？

解析：设使用年的年平均费用为万元　　　　　　　 则使用年的维修总费用为 万元　　

　 依题得 　　

　　　　　　　　 -　

当且仅当 即时取等号 时取得最小值3 万元　　　　　　　　　　　 答：这种汽车使用10年时，它的年平均费用最小，最小值是3 万元.

★ 抢 分 频 道 ★

基础巩固训练

6.已知函数，若在(0，+)上恒成立，求的取值范围。

解析：因为在(0，+)上恒成立，即

∴　 　　　　　∵ 的最小值为4　　　 ∴　

解得

5.设x>0,y>0且x≠y,求证

证明：由x>0,y>0且x≠y,要证明

只需　　　 即

只需

由条件,显然成立.∴原不等式成立

考点3 基本不等式在实际中的应用

题型1.处理恒成立的有关问题

例1. (2008·中山)若,且恒成立,则的最小值是________

[解题思路]分离系数得令求最大值即可

解析: 事实上求函数的最大值,即的最大值,运用基本不等式不难得到.

[名师指引]分离系数法是处理参数取值范围的常用方法.

题型2.处理函数应用题

.例2.(2008·梅县)某厂生产某种产品的年固定成本为250万元,每生产千件,需另投入成本为.当年产量不足80千件时,(万元);当年产量不小于80千件时,(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.

(1)写出年利润(万元)关于年产量(千件)的函数解析式;

(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?

[解题思路]凑出基本不等式的形式.

解析: (1)当时,

当时,

∴

(2)当时,,此时,当时,取得最大值(万元);

当时,

此时,当时,即时,取得最大值1000万元.

所以,当产量为100千件时,该厂在这一商品中所获利润最大,最大利润为1000万元.　　　

[名师指引]形如函数的形式求最值时可考虑用基本不等式，但要注意条件的限制,可借助函数的图像解题，必要时借助于导数.

题型3.处理数列应用题

例3. 某乡为提高当地群众的生活水平,由政府投资兴建了甲、乙两个企业,2007年该乡从甲企业获得利润320万元,从乙企业获得利润720万元.以后每年上交的利润是：甲企业以1.5倍的速度递增,而乙企业则为上一年利润的.根据测算,该乡从两个企业获得的利润达到2000万元可以解决温饱问题,达到8100万元可以达到小康水平.

(1)若以2007年为第一年,则该乡从上述两个企业获得利润最少的一年是那一年,该年还需要筹集多少万元才能解决温饱问题？

(2)试估算2015年底该乡能否达到小康水平？为什么？

[解题思路]经审题抽象出数列模型

[解析](Ⅰ)若以2007年为第一年,则第n年该乡从这两家企业获得的利润为

　　 ==

　 当且仅当,即n=2时,等号成立，

所以第二年(2008年)上交利润最少，利润为960万元.

由2000–960=1040(万元)知：还需另筹资金1040万元可解决温饱问题.

(Ⅱ)2015年为第9年,该年可从两个企业获得利润

所以该乡到2015年底可以达到小康水平.

[名师指引]本题重点考查数列的相关知识,基本不等式起到了工具性的作用.

[新题导练]