4.已知,求证:

解析：∵ ∴①　 又∵②　 ③

　 由①②③得 ∴,又不等式①、②、③中等号成立的条件分别为,,故不能同时成立,从而.

3. 已知一动直线与两坐标轴的正半轴围成的三角形的面积的数值比直线的纵、横截距之和大1，求这三角形面积的最小值．

解析：　 设直线的方程(a>0，b>0)，则，∵a+b>2，

∴≥，即≥0，解得≥，

∴≥，当a=b=2+时，三角形面积的最小值为5+2

考点2　 利用基本不等式证明

题型：用综合法证明简单的不等式

例1.　　　　　　 已知,求证:.

[解题思路]因为是轮换对称不等式，可考虑由局部证整体.

[解析] ,

相加整理得.

　 当且仅当时等号成立.

[名师指引]综合法证明不等式常用两个正数的算术平均数不小于它们的几何平均数这一结论，运用时要结合题目条件，有时要适当变形.

例2. 已知a，b为正数，求证：≥．

[解题思路]观察结构用基本不等式加以证明.

解析1：∵ a>0，b>0，

∴ ≥，

　 ≥，

两式相加，得

≥，

∴ ≥．

解析2. ≥

．

∴≥．

解析3.∵ a>0，b>0，∴，

∴ 欲证 ≥，

即证 ≥，

只要证　 ≥，

只要证　 ≥，

即证　 ≥，

只要证 a³+b³≥ab(a+b)，

只要证 a²+b²-ab≥ab，

即证 (a-b)²≥0．

∵ (a-b)²≥0成立，∴ 原不等式成立 ．

[名师指引]当要证明的不等式形式上比较复杂时，常通过分析法寻求证题思路．

“分析法”与“综合法”是数学推理中常用的思维方法，特别是这两种方法的综合运用能力，对解决实际问题有重要的作用． 这两种数学方法是高考考查的重要数学思维方法．

[新题导练]

2. .(2008·华附)已知则的最小值为　　　　　

解析:∵，当且仅当时取等号.

1.若，则=_____时,有最小值，最小值为_____.

解析:∵, ∴, ∴,∴=

，当且仅当即时.

4．已知试从几何变换的角度求解矩阵的逆矩阵.

3．已知曲线C₁的参数方程为(为参数)，曲线C₂的极坐标方程为，曲线C₁、C₂交于点A、B

　 (1)求A、B两点的极坐标

　 (2)求弦AB的长度

2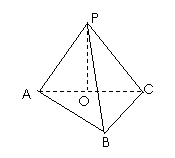．如图，在三棱锥P-ABC中，AB⊥BC，AB=BC=kPA，点O是AC的中点，OP⊥底面ABC

　 (1)当k=时，求PA与平面PBC所成角的正弦值

　 (2)当k取何值时，O在平面PBC内的射影恰好是△PBC的重心

1．一个博彩者，放6个白球，6个红球在一个袋子中，定下规则：凡愿摸彩者，每人交1元钱，然后可以从袋中摸出5个球，中彩情况如下表：

试计算：

　 (1)摸一次能获得20元奖品的概率；

　 (2)按摸10000次统计，这个博彩者能否赚钱，如果赚钱，求净赚多少钱？(精确到元)

20．(本题满分18分，第1题6分，第2题6分，第3题6分)

已知函数f(x)=e^x－x(e为自然对数的底数)，

　 (1)求f(x)的最小值；

　 (2)设不等式f(x)>－ax的解集为P，且{x|0≤x≤2}P，求实数a的取值范围；

　 (3)设n∈N*，探究的整数部分的值，并证明你的结论。

东台市三仓中学2008届高三考前抢分练习一

数 学 附 加 题 部 分

19．(本题满分16分，第1题4分，第2题6分，第3题6分)

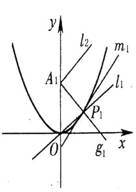已知函数y=x²的图象为曲线C，过原点作斜率为1的直线l₁与曲线C在第一象限交于点P₁，曲线C在点P₁处的切线为m₁，过点P₁且与m₁垂直的直线g₁交y轴于A₁(0，a₁)，又过A₁作l₁的平行线l₂与曲线C在第一象限交于点P₂，曲线C在点P₂处的切线为m₂，过点P₂且与m₂垂直的直线g₂交y轴于A₂(0，a₂)，……，依此继续下去：过点A_n(0, a_n)作与l_n平行的直线l_n+1与曲线C在第一象限交于点P_n+1，曲线C在点P_n+1处的切线为m_n+1，过点P _n+1与且m _n+1垂直的直线g _n+1交y轴于点A _n+1 (0, a _n+1)。

(1)求a₁ ；

(2)求a _n+1关于a _n的函数解析式a _n+1=f(a _n)，(其中n∈N*)；

(3)①证明：a_n>(+)²；并利用①证明a_n>

②证明：a­_n<3×2^n-1-