20. (本题满分16分)已知函数.

(1)若函数图象上任意一点处的切线的倾斜角均不小于，求实数的取值范围；

(2)设，若存在，不等式成立，求实数的取值范围；

(3)已知，试讨论关于的方程在区间上的实根的个数.(参考数据： 　)

2009-2010学年度第二学期高二期中考试

19. (本题满分16分)袋中装有黑球和白球共7个，从中任取2个球都是白球的概率为，现在甲、乙两人从袋中轮流摸取1球，甲先取，乙后取，然后甲再取……取后不放回，直到两人中有一人取到白球时即止，每个球在每一次被取出的机会是等可能的，用表示取球终止时所需要的取球次数．

(1)求袋中原有白球的个数；

(2)求随机变量的概率分布；

(3)求甲取到白球的概率．

18．(本题满分16分)等差数列的前项和为，，.

(1)求数列的通项与前项和；

(2)设，求证数列中任意不同的三项都不可能构成等比数列.

17．(本题满分14分)已知正项数列和中，₁ = (),　当≥2时，　

(1)证明：对任意有；

(2)求数列的通项公式.

16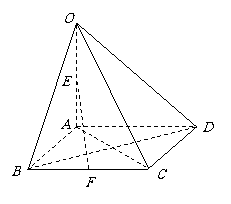．(本题满分14分)在四棱锥中，底面为菱形，⊥平面，为的中点，为的中点，求证：

(1)平面⊥平面；

(2)// 平面.

15．(本题满分14分)已知的展开式中，某一项的系数是它前一项系数的2倍，而又等于它后一项系数的.

(1)求展开后所有项的系数之和及所有项的二项式系数之和；

(2)求展开式中的有理项.

14．已知复数(其中i为虚数单位)，若对一切恒成立，则实数a的取值范围为　　 ▲　　 　.

第二卷

13．已知命题：若数列为等差数列，且，，则.那么对于数列为等比数列，且，，则可得到　　 ▲　　 　.

12．若直线是曲线上一点处的切线，则实数的值为　　 ▲　　 　.

11．设，，，…，，，则

　　 ▲　　 　.