20．(本小题满分14分)

已知抛物线：的焦点为，过点作直线交抛物线于、两点；椭圆的中心在原点，焦点在轴上，点是它的一个顶点，且其离心率．

(1)求椭圆的方程；

(2)经过、两点分别作抛物线的切线、，切线与相交于点．证明：；

(3) 椭圆上是否存在一点，经过点作抛物线的两条切线、(、为切点)，使得直线过点？若存在，求出抛物线与切线、所围成图形的面积；若不存在，试说明理由．

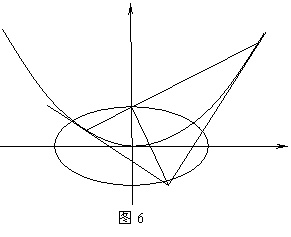
19．(本小题满分14分)

设函数(，)．

(1)若函数在其定义域内是减函数，求的取值范围；

(2)函数是否有最小值？若有最小值，指出其取得最小值时的值，并证明你的结论．

18．(本小题满分14分)

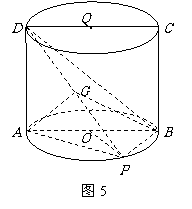
如图5，四边形是圆柱的轴截面，点在圆柱的底面圆周上，是的中点，圆柱的底面圆的半径，侧面积为，．

(1)求证：；

(2)求二面角的平面角的余弦值．

17．(本小题满分12分)

上海世博会深圳馆1号作品《大芬丽莎》是由大芬村507名画师集体创作的999幅油画组合而成的世界名画《蒙娜丽莎》，因其诞生于大芬村，因此被命名为《大芬丽莎》．某部门从参加创作的507名画师中随机抽出100名画师，测得画师年龄情况如下表所示．

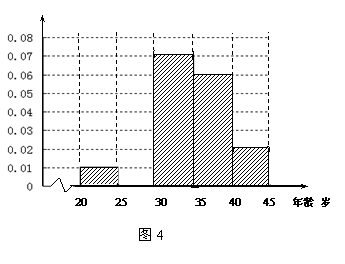
(1)频率分布表中的①、②位置应填什么数据？并在答题卡中补全频率分布直方图(图4)，再根据频率分布直方图估计这507个画师中年龄在岁的人数(结果取整数)；

(2)在抽出的100名画师中按年龄再采用分层抽样法抽取20人参加上海世博会深圳馆志愿者活动，其中选取2名画师担任解说员工作，记这2名画师中“年龄低于30岁”的人数为ξ，求ξ的分布列及数学期望．

分组 (单位：岁)	频数	频率
	5	0.050
	①	0.200
	35	②
	30	0.300
	10	0.100
合计	100	1.00

16．(本小题满分12分)

已知，，设．

(1)求函数的最小正周期及其单调递增区间；

(2)若分别是锐角的内角的对边，且，，试求的面积．

(二)选做题(14、15题，考生只能从中选做一题)

14．(坐标系与参数方程选做题)

在极坐标系中，若圆的极坐标方程为，若以极点为原点，以极轴为轴的正半轴建立相应的平面直角坐标系中，则在直角坐标系中，圆心的直角坐标是　　　　 ．

15．(几何证明选讲选做题)

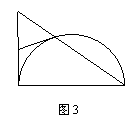
如图3，在中，，以为直径作半圆交于，过作半圆的切线交于，若，，则=　　 　　　．

(一)必做题(9-13题)

9．设全集，则a的值为　　　　　 ．

10．在的展开式中，项的系数是　　　　　 ．

11．已知双曲线的两条渐近线的夹角为，则双曲线的离心率为

　　　　　 ．

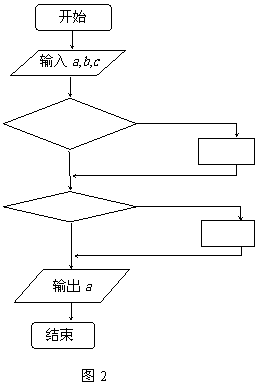
12．给出以下一个算法的程序框图(图2)，如果，，，则输出的结果是　　　　 ．(注：框图中的的赋值符号“＝”也可以写成“←”或“：＝”)

13．设是边长为的正内的一点，点到三边的距离分别为，则；类比到空间，设是棱长为的空间正四面体内的一点，则点到四个面的距离之和=　　　　　 ．

8．将长度为1的线段随机折成三段，则三段能构成三角形的概率是

A．　　　　　　　　　　　　　 B．　　　　　　　　　　　　　 C．　　　　　　　　　　　　　 D．

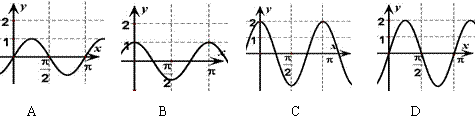
7．已知是实数，则函数的导函数的图象可能是

6．设，，则以下不等式中，不恒成立的是

A．

B．

C．

D．