12．为了减少运费，最需要接近市场的是(　　 )

A. 制糖厂　　　 B. 造船厂　　　　 C　 瓶装饮料厂　 D . 普通服装厂

11．下列企业属于动力指向型工业的是(　　 )

A．炼铝厂　　　 B．水产品加工厂　　 C．服装厂　　 D．电子元件厂

10．农民扩大或缩小某种农产品种植面积最终取决于(　　 )

A．气候　　　　　 B．市场　　　 C．地形　　　 　 D．交通运输

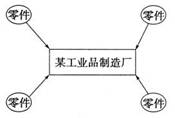读右图，图中椭圆代表分布于不同国家的零件生产厂家。完成8-9题。

8．图中所示的工业部门可能是(　 )

C．飞机制造工业　 　D．钢铁冶炼工业

9．该工厂的零部件生产出现了全球化趋势。这样做的最终目的是(　 　)

A．增加产品的国际化程度，从而更好地被世界各国人选购

B．充分发挥各地优势，降低生产成本，提高经济效益

C．带动相关各国经济的发展，从而促进全球经济水平的提高

D．跨国公司为显示其实力，从而提高某品牌知名度

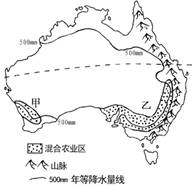
读“某区混合农业分布图”，回答6-7题。

6．关于图中混合农业区的叙述正确的是(　)

　　 ①小麦种植业和牧羊业混合经营

②甘蔗、果树种植和养鱼有机结合

③实行牧草与作物轮作

④投入大量廉价劳动力精耕细作

A．①③　 　B．①④　 C．②③　 D．②④

7．该区东南部混合农业经营的主要限制因素是(　)

A．多山地丘陵、耕地面积小　　　　 B．气候炎热干燥、蒸发旺盛

C．处于大分水岭的背风坡，降水少，水源不足　　　　 D．土壤贫瘠

近年来，北京和天津政府相继做出决定，停止两市的水稻种植，将原有的稻田改种玉米和小麦。据此回答3-5题。

3.政府做出此项决定的主要原因是(　)

A．稻米生产过剩，价格太低　　　　　　 B．水稻产量低于玉米和小麦

C．为了节约水资源　　　　　　　　　　 D．北方居民习惯吃面食

4.上述材料所体现出的影响农业的区位因素是(　)

A．技术　　　 B．市场　　 　C．交通运输　　　 D．政府政策

5.关于我国商品谷物农业的叙述正确的是 (　　 )

A．我国商品谷物农业主要分布在黄淮海平原

B．我国商品谷物农业主要分布在地广人稀的东北和西北

C．我国商品谷物农业的经营模式与国外一致--由农场主经营

D．我国商品谷物农业种植的主要是水稻和玉米

2．珠江三角洲的花卉种植业，从投入多少分，属于(　　 )

A．密集农业　　　 B．粗放农业　　　 C．自给农业　　 D．商品农业

1．能反映农业生产特点正确的是(　　 )

A．人误地一时，地误人一年--主观性　　

　B．离离原上草，一岁一枯荣--地域性

C. 橘生淮南则为橘，生于淮北则为枳-- 灵活性　

　D. 白露早，寒露迟，秋分种麦正当时--季节性

21、三次函数f(x)=x³+ax²+bx+a²在x=1处有极值0

①求函数f(x)的解析式　

②求它的对称中心的横坐标(无需证明)

③(理)过异于对称中心的任一点P₁(x₁,y₁)作f(x)图像的切线，切于另一点P₂(x₂,y₂)，再过P₂(x₂,y₂)作f(x)图像的切线，和f(x)切于点P₃(x₃,y₃)，如此下去，得到P₄(x₄,y₄)、P₅(x₅,y₅)、···、P_n(x_n,y_n)，求当次数n不断增大时P_n 的横坐标趋近于哪一个数？

[答案与解析]

16解：①令代入中得。(4分)

　　　 ②令代入中得(6分)　　　　　　

不等式化为；

又函数是定义在上的增函数，所以

得(12分)

17解：①由题意得f'_x(3,4)=6

f'_y(3,4)=8(6分)

　　　 ②由几何意义可求得z的最小值为(12分)

18解：①由题意，贷款额，利息。(4分)

　　　 ②李佳节省的钱(设为y)即为两种付款方式之间的利息差，则: ，所以

　 令解得，从而时，；时，。

　　　 所以，当时，函数取到最大值，即

银行贷款利率为时，李佳可以节省最多的钱。(12分)

19解：由于f(x)=(x-)+ -

　　　 于是若∈[0 ,1 ] ,即0 ≤a ≤2 ,则最小值为-

(3分)

若不属于[0 ,1 ]则最小值为f(0)和f(1)中的最小者。(6分)

所以F(a)：

当0 ≤a ≤2时为-

当a>2时为1-

　　　　 以下由二次函数知识可以求得当a = 1 时, F( a) 达到最大值(12分)

20解：对任意的，不等式恒成立，即，则恒成立。(3分)

　　 当时，对任意的x不恒成立。(6分)

　　 当时，对任意的x不等式不能恒成立。

(9分)

当时，对任意的x不等式恒成立，则，即(12分)

综上所述，实数a的取值范围是(13分)

21解：①由题意得：

(2分，文科4)

解之得：(4分，文科8分)

于是f(x)=x³+4x²-11x+16或f(x)=x³-3x²+3x+9

检验，当f(x)=x³-3x²+3x +9时，此时，尽管满足了，但在1的左右两侧的导数符号为同号，亦即x=1不是f(x)=x³-3x²+3x+9的极值点。

∴f(x)=x³+4x²-11x+16(6分，文科10分)

②易求得其极值点为x=1和x=-，因而对称中心横坐标-(8分，文科14分)

，设直线P_nP_n-1是过点P_n且与f(x)的图像切于点P_n-1的切线，则一方面切线的斜率为，另一方面切线的斜率为：

=

所以即

　　 又因为，所以，即。

利用待定系数法易知：，故数列为等比数列，所以，即

，

则，不难看出当n 时，点列P₁、P₂、P₃……P_n横坐标趋近于对称中心横坐标-(14分)

20、已知函数，a为常数。如果对任意的，不等式恒成立，求实数a的取值范围。