
5.函数 图象的对称轴方程可以为
图象的对称轴方程可以为
A. B.
B.  C.
C.  D.
D.

4.已知直线 ,则
,则 之间的距离为
之间的距离为
A.1
B. C.
C.
 D.
D.

3. 已知a= ,b=
,b= ,若
,若 ,则
,则 的值为
的值为
A.  B.
B. C.
C.  D.
D. 
2.双曲线 的焦距为
的焦距为
A.10
B. C.
C.
 D. 5
D. 5
1.已知集合 ,
, ,则
,则

A. B.
B. C.
C. D.
D.
(15)(本题满分13分)
设函数 .
.
(Ⅰ)求函数 的最小正周期;
的最小正周期;

(Ⅱ)当 时,求函数
时,求函数 的最大值及取得最大值时的
的最大值及取得最大值时的 的值.
的值.
(16)
(本题满分1 3分)
3分)
某运动员进行20次射击练习,记录了他射击的有关数据,得到下表:
|
环数 |
7 |
8 |
9 |
10 |
|
命中次数 |
2 |
7 |
8 |
3 |
(Ⅰ)求此运动员射击的环数的平均数;
(Ⅱ)若将表中某一环数所对应的命中次数作为一个结果,在四个结果(2次、7次、8次、3次)中,随机取2个不同的结果作为基本事件进行研究,记这两个结果分别为 次、
次、 次,每个基本事件为(m,n).
次,每个基本事件为(m,n).
求“ ”的概率.
”的概率.
(17) (本题满分13分)
如图,在四棱锥 中,底面
中,底面 是正方形,其他四个侧面都是等边三角形,
是正方形,其他四个侧面都是等边三角形, 与
与 的交点为O.
的交点为O.
(Ⅰ)求证: 平面
平面 ;
;
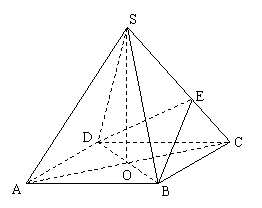 (Ⅱ)已知
(Ⅱ)已知 为侧棱
为侧棱 上一个动点. 试问对于
上一个动点. 试问对于 上任意一点
上任意一点 ,平面
,平面 与平面
与平面 是否垂直?若垂直,请加以证明;若不垂直,请
是否垂直?若垂直,请加以证明;若不垂直,请 说明理由.
说明理由.
(18) (本题满分14分)
已知函数 ,
,
 ,且
,且 .
.
(Ⅰ)若 ,求
,求 的值;
的值;
(Ⅱ)当 时,求函数
时,求函数 的最大值;
的最大值;
(Ⅲ)求函数 的单调递增区间.
的单调递增区间.
(19) (本题满分13分)
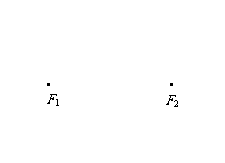 已知椭圆
已知椭圆 的左右焦点分别
的左右焦点分别 为
为 ,
, .在椭圆
.在椭圆 中有一内接三角形
中有一内接三角形 ,其顶点
,其顶点 的坐
的坐 标
标 ,
, 所在直线的斜率为
所在直线的斜率为 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)当 的面积最大时,求直线
的面积最大时,求直线 的方程.
的方程.
20.(本题满分14分)
已知 是递增数列,其前
是递增数列,其前 项和为
项和为 ,
, ,
, 且
且 ,
, .
.
(Ⅰ)求数列 的通项
的通项 ;
;
(Ⅱ)是否存在 ,使得
,使得 成立?若存在,写出一组符合条件的
成立?若存在,写出一组符合条件的 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(Ⅲ)设 ,若对于任意的
,若对于任意的 ,不等式
,不等式
 恒成立,求正整数
恒成立,求正整数 的最大值.
的最大值.
(9)函数 的值域是
.
的值域是
.
 (10)已知向量
(10)已知向量 ,
, ,如果
,如果 与
与 垂直,那么实数
垂直,那么实数
 的值为
.
的值为
.
(11)设变量 ,
, 满足
满足
则该不等式组所表示的平面区域的面积等于
; 的最大值为
.
的最大值为
.
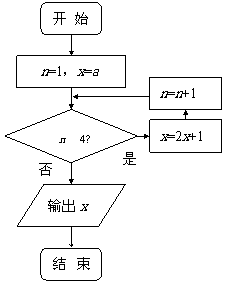
(12)若某程序框图如右图所示,
该程序运行后,输出的 ,
,
则 等于
.[来源:]
等于
.[来源:]
 (1
(1 3)上海世博园中的世博轴是一条1000
3)上海世博园中的世博轴是一条1000 长的直线型通道,中国馆位于世博轴的一侧(
长的直线型通道,中国馆位于世博轴的一侧( 如下图所示). 现测得中国馆到世博轴两端的距离相等,并且从中国馆看世博轴两端的视角为
如下图所示). 现测得中国馆到世博轴两端的距离相等,并且从中国馆看世博轴两端的视角为 . 据此数据计算,中国馆到世博轴其中一端的距离是
. 据此数据计算,中国馆到世博轴其中一端的距离是
 .
.
(14)已知数列 为等差数列,若
为等差数列,若
 ,
, (
( ,
, ),则
),则 .
.
类比等差数列的上述结论,对等比数列 (
( ,
, ),若
),若 ,
,
( ,
, ),则可以得到
),则可以得到 =
.
=
.
(1)已知集合 ,集合
,集合 ,集合
,集合 ,则
,则
等于
(A) (B)
(B) (C)
(C) (D)
(D)
(2)设 为虚数单位,则复数
为虚数单位,则复数 所对应的点位于
所对应的点位于
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
(3)过点 引圆
引圆 的切线,则切线长是
的切线,则切线长是
(A) 2 (B) (C)
(C)  (D)
(D) 
(4)一个正方体的所有顶点都在同一球面上,若球的体积是 ,则正方体的表面积是
,则正方体的表面积是
(A)8 (B)6 (C)4 (D)3
(5)某校共有学生2000名,各年级男、女学生人数如下表,已知在全校学生中随机抽取1名,抽到二年级女生的概率是0.19,现用分层抽样的方法在全校学生中抽取64人,则应在三年级抽取的学生人数为 ( )
( )
|
|
一年级 |
二年级 |
三年级 |
|
女生 |
385 |
 |
 |
|
男生 |
375 |
360 |
 |
(A) (B)
(B) (C)
(C) (D)
(D)
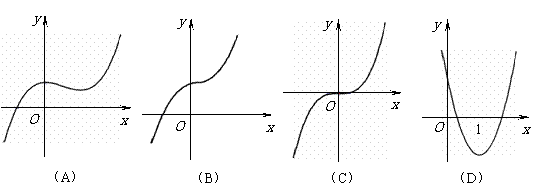 (6)函数
(6)函数 的图象大致是
的图象大致是
(7)一个几何体的三视图如图所示,则此几何体的体积是
(A) (B)
(B)
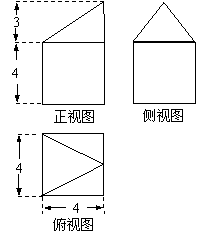 (C)
(C) (D)
(D)
(8)如图所示, 是定义在区间
是定义在区间 (
( )上的奇函数,令
)上的奇函数,令 ,并有关于函数
,并有关于函数 的四个论断:
的四个论断:
①对于 内的任意实数
内的任意实数 (
( ),
), 恒成立;
恒成立;
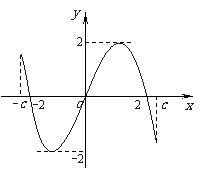 ②若
②若 ,则函数
,则函数 是奇函数;
是奇函数;
③若 ,
, ,则方程
,则方程 必有3个实数根;
必有3个实数根;
④若 ,则
,则 与
与 有相同的单调性.
有相同的单调性.
其中正确的是( )
(A)②③ (B)①④
(C)①③ (D)②④
第II卷(非选择题 共110分)
(15)(共12分)
解:(Ⅰ)由已知得: .
.
∵ 为锐角
为锐角
∴ .
.
∴  .
.
∴ .--------------------6分
.--------------------6分
(Ⅱ)∵
∴ .
.
 为锐角,
为锐角,
∴ ,
,
∴ .
.  -----------12分
-----------12分
(16)(共14分)
(Ⅰ)连接 ,在
,在 中,
中,
∵ 为
为 的中点,
的中点, 为
为 的中点,
的中点,
∴
 ∥
∥
又∵ 平面
平面
∴直线 ∥平面
∥平面 .
--------------------4分
.
--------------------4分
(Ⅱ)在正方体 中,
中,
 平面
平面 ,
,
 平面
平面
∴ .
.

且
∴
∴
同理可证
∵
∴ 平面
平面 .
--------------------9分
.
--------------------9分
(Ⅲ) . -------------14分
. -------------14分
(17)(共13分)
解:(Ⅰ)若 ,
, ,则点
,则点 的个数共有
的个数共有 个,列举如下:
个,列举如下:
 ;
; ;
;
 ;
; ;
;
 .
.
当点 的坐标为
的坐标为 时,点
时,点 位于第四象限.
位于第四象限.
故点 位于第四象限的概率为
位于第四象限的概率为 . ---------------- 6分
. ---------------- 6分
(Ⅱ)由已知可知区域 的面积是
的面积是 .
.
因为直线 与圆
与圆 的
的 弦长为
弦长为 ,
,
如图,可求得扇形的 圆心角为
圆心角为 ,
,
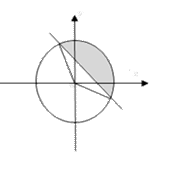 所以扇形的面积为
所以扇形的面积为 ,
,
则满足 的点
的点 构成的区域的面积为
构成的区域的面积为

 ,
,
所以 的概率为
的概率为
 .---------------- 13分
.---------------- 13分
(18)(共14分)
解:(Ⅰ) ,由题意:
,由题意:
 即
即 解得
解得
∴ ,
,
令 ,解得
,解得 ;
;
令 ,解得
,解得 或
或 ,
,
∴ 的减区间为
的减区间为 ;增区间为
;增区间为 ,
, .---------------5
.---------------5 分
分
(Ⅱ)由(Ⅰ)知, 在
在 上单调递增;
上单调递增;
在 上单调递减; 在
上单调递减; 在 上单调递增.
上单调递增.
∴ 时,
时, 的最大值即为
的最大值即为 与
与 中的较大者.
中的较大者.
 ;
; 
∴当 时,
时, 取得最大值.
取得最大值.
要使 ,只需
,只需 ,即:
,即:
解得: 或
或 .
.
∴ 的取值范围为
的取值范围为 . -------------14分
. -------------14分
(19)(共14分)
 解:(Ⅰ)设椭圆方程为
解:(Ⅰ)设椭圆方程为
由已知可得 ,解得
,解得  .
.
所求椭圆的 方程为
方程为  . -------
. ------- ------5分
------5分
(Ⅱ)设
当直线 与
与 轴不垂直时,设直线
轴不垂直时,设直线 的方程为
的方程为 .
.

 ,
, ,
,






 是与
是与 无关的常数
无关的常数 ,
,
∴
∴ ,即
,即 .
.
此时, .
.
当直线 与
与 轴垂直时,则直线
轴垂直时,则直线 的方程为
的方程为 .
.
此时点 的坐标分别为
的坐标分别为
当 时, 亦有
时, 亦有
综上,在 轴上存在定点
轴上存在定点 ,使
,使 为常数.------------ 14分
为常数.------------ 14分
(20)(共13分)
解:(Ⅰ)由 ,得
,得 ,
,
所以 ,故{
,故{ }是等差数列.---------------- 4分
}是等差数列.---------------- 4分
(Ⅱ) 由(Ⅰ)知,  ,所以
,所以 .
.

所以 ------------
------------ ---- 9分
---- 9分
(Ⅲ)
所以
 …
…
 …
… . ---
. --- -------1 3分
-------1 3分
(9) (10)
(10) (11
(11 )
) ;
;
(12) (13)①,④
(14)
(13)①,④
(14)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com