5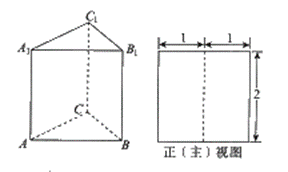．如图，三棱柱ABC-A₁B₁C₁的侧棱长和底面边长均为2，且侧棱底面ABC，其正(主)视图是边长为2的正方形，则此三棱柱侧(左)视图的面积为　 (　　 )

　　　 A．

　　　 B．

　　　 C．

　　　 D．4

4．“”是“”的　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．充分非必要条件

　　　 B．必要非充分条件

　　　 C．充要条件　　　　　

　　　 D．既不充分也不必要条件

3．设变量满足约束条件，则目标函数的最小值为　　　 (　　 )

　　　 A．1　　　　　　　　　　　　 B．2　　　　　　　　　　　　 C．3　　　　　　　　　　　 D．4

2．已知命题，则　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．　　　　　　　　　　　 B．

　　　 C．　　　　　　　　　　　 D．

1．设集合，则等于　　　　　　　　　　　　　　 (　　 )

　　　 A．2　　　　　　　　　　　　 B．3　　　　　　　　　　　　 C．4　　　　　　　　　　　 D．6

20．(本小题满分13分)

给定椭圆，称圆心在原点，半径为的圆是椭圆C的“准圆”.若椭圆C的一个焦点为，其短轴上的一个端点到F的距离为.

(I)求椭圆C的方程和其“准圆”方程；

(II )点P是椭圆C的“准圆”上的一个动点，过点P作直线，使得与椭圆C都只有一个交点，且分别交其“准圆”于点M，N .

(1)当P为“准圆”与轴正半轴的交点时，求的方程；

(2)求证：|MN|为定值.

海淀区高三年级第二学期期末练习

19．(本小题满分14分)

已知函数，

(I)当时，求函数的极值；

(II)若函数在区间上是单调增函数，求实数的取值范围.

18．(本小题满分13分)

若数列满足，为数列的前项和.

(Ⅰ) 当时，求的值；

(Ⅱ)是否存在实数，使得数列为等比数列？若存在，求出满足的条件；若不存在，说明理由.

17．(本小题满分14分)

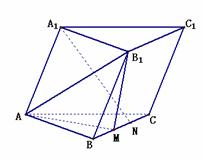在斜三棱柱中，侧面平面， .

(I)求证：；

(II)若M,N是棱BC上的两个三等分点，

求证：平 面.

16．(本小题满分13分)

某园林局对1000株树木的生长情况进行调查，其中槐树600株，银杏树400株. 现用分层抽样方法从这1000株树木中随机抽取100株，其中银杏树树干周长(单位:cm)的抽查结果如下表：

树干周长(单位:cm)
株数	4	18		6

(I)求的值 ;

(II)若已知树干周长在30cm至40cm之间的4株银杏树中有1株患有虫害,现要对这4株树逐一进行排查直至找出患虫害的树木为止.求排查的树木恰好为2株的概率.