
3.[必做题](本题满分10分)
如图所示的几何体是由以等边三角形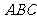 为底面的棱柱被平面
为底面的棱柱被平面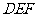 所截而得,已知
所截而得,已知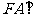 平面
平面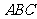 ,
,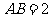 ,
,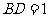 ,
,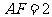 ,
,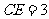 ,
,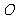 为
为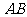 的中点.
的中点.
(Ⅰ)求证: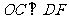 ;
;
(Ⅱ)求平面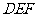 与平面
与平面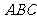 相交所成锐角二面角的余弦值;
相交所成锐角二面角的余弦值;
(Ⅲ)在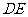 上是否存在一点
上是否存在一点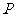 ,使
,使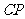
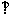 平面
平面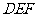 ?如果存在,求出
?如果存在,求出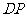 的长;若不存在,说明理由.(选自福州三中第三次月考理)
的长;若不存在,说明理由.(选自福州三中第三次月考理)
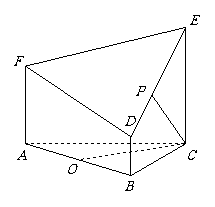
提示:如图,以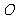 为原点,
为原点,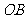 ,
,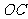 ,
,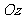 分别为
分别为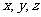 轴建立空间直角坐标系,
轴建立空间直角坐标系,
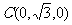 ,
,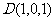 ,
,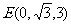 ,
,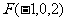 . ……2分
(Ⅰ)
. ……2分
(Ⅰ)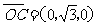 ,
,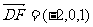 ,
所以
,
所以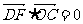 ,即
,即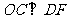 . ……2分
(Ⅱ)平面
. ……2分
(Ⅱ)平面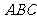 的法向量为
的法向量为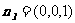 .
设平面
.
设平面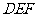 的法向量为
的法向量为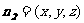 ,
,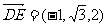 .
由
.
由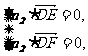 得
得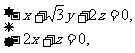 所以
所以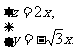 取
取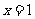 ,得
,得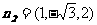 .
所以
.
所以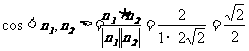 ,所以平面
,所以平面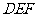 与平面
与平面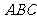 相交所成锐角二面角的余弦值为
相交所成锐角二面角的余弦值为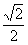 . ……6分
(Ⅲ)假设在
. ……6分
(Ⅲ)假设在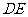 存在一点
存在一点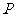 , 设
, 设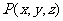 ,
因为
,
因为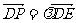 ,故
,故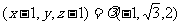 ,
所以
,
所以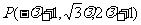 ,所以
,所以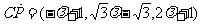 .
因为
.
因为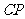
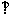 平面
平面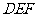 ,所以
,所以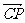 与平面
与平面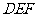 的法向量
的法向量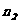 共线,
所以
共线,
所以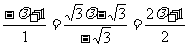 ,解得
,解得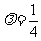 ,
所以
,
所以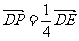 ,即
,即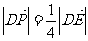 ,所以
,所以 . ……10分
. ……10分
点评:该题考查空间向量的坐标表示、空间向量的数量积、空间向量的共线与垂直、直线的方向向量与平面的法向量;是中档题。
2.[必做题](本题满分10分)
某单位举办2010年上海世博会知识宣传活动,进行现场抽奖.盒中装有9张大小相同的精美卡片,卡片上分别印有“世博会会徽”或“海宝”(世博会吉祥物)图案;抽奖规则是:参加者从盒中抽取卡片两张,若抽到两张都是“海宝”卡即可获奖,否则,均为不获奖.卡片用后放回盒子,下一位参加者继续重复进行.
(I)有三人参加抽奖,要使至少一人获奖的概率不低于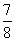 ,则“海宝”卡至少多少张?
,则“海宝”卡至少多少张?
(Ⅱ)现有甲乙丙丁四人依次抽奖,用 表示获奖的人数,求
表示获奖的人数,求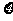 的分布列及
的分布列及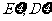 的值.(北京市宣武区理改编)
的值.(北京市宣武区理改编)
提示:(I)记至少一人获奖事件为A,则都不获奖的事件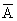 ,设“海宝”卡n张,则任一人获奖的概率
,设“海宝”卡n张,则任一人获奖的概率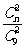 ,所以,
,所以, 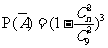 ,由题意:
,由题意: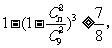 所以,
所以,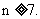
至少7张“海宝”卡………………………………………………4分
(Ⅱ) -
-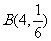 的分布列为
的分布列为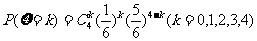 ;
;
 |
0 |
1 |
2 |
3 |
4 |
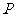 |
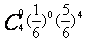 |
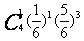 |
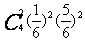 |
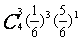 |
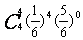 |
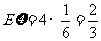 ,
,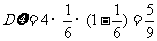 .…………………………………………10分
.…………………………………………10分
点评:该题考查乘法原理、排列组合、二项式定理、n次独立重复试验的模型及二项分布,是中档题。
1.已知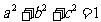 ,若
,若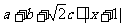 对任意实数a,b,c恒成立,求实数x的取值范围. (选自福建上杭一中12月月考理)
对任意实数a,b,c恒成立,求实数x的取值范围. (选自福建上杭一中12月月考理)
提示: 
 …………………………………………5分
…………………………………………5分
又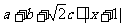 对任意实数a,b,c恒成立,
对任意实数a,b,c恒成立,
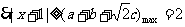
解得 ………………………………………10分
………………………………………10分
点评:该题考查柯西不等式、绝对值不等式求解;是容易题。
22.(本小题满分12分)
已知函数f (x)=ln(1+x)+a (x+1)2 (a为常数).
(Ⅰ)若函数f (x)在x=1处有极值,判断该极值是极大值还是极小值;
(Ⅱ)对满足条件a≤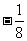 的任意一个a,方程f (x)=0在区间(0,3)内实数根的个数是多少?
的任意一个a,方程f (x)=0在区间(0,3)内实数根的个数是多少?
21.(本小题满分12分)
已知函数f (x)=alnx+x2 (a为实常数).
(Ⅰ)若a=-2,求证:函数f (x)在(1,+∞)上是增函数;
(Ⅱ)求函数f (x)在[1,e]上的最小值及相应的x值;
(Ⅲ)若当x∈[1,e]时,f (x)≤(a+2)x恒成立,求实数a的取值范围.
20.(本小题满分12分)
在一次体操选拔赛中,教练组设置了难度不同的甲、乙两个系列,每个系列都有A和B两个动作.比赛时每位运动员自选一个系列完成,两个动作得分之和为该运动员的成绩.
假设每个运动员完成每个系列中的两个动作的得分是相互独立的.根据赛前训练统计数据,某运动员完成甲系列和乙系列的情况如下表:
表1:甲系列 表2:乙系列
现该运动员最后一个出场,之前其他运动员的最高得分为115分.
(Ⅰ)若该运动员希望获得该项目的第一名,应选择哪个系列?说明理由,并求其获得第一名的概率;
(Ⅱ)若该运动员选择乙系列,求其成绩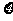 的分布列及其数学期望
的分布列及其数学期望 .
.
19.(本小题满分12分)
用半径为R的圆形铁皮剪出一个圆心角为α的扇形,制成一个圆锥形容器,求:扇形的.圆心角多大时,容器的容积最大?并求出此时容器的最大容积.
18.(本小题满分12分)
现有三人被派去各自独立地解答一道数学问题,已知三人各自解答出的问题概率分别为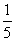 ,
,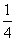 ,
,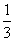 ,且他们是否解答出问题互不影响.
,且他们是否解答出问题互不影响.
(Ⅰ)求恰有二人解答出问题的概率;
(Ⅱ)求“问题被解答”与“问题未被解答”的概率.
17.(本小题满分10分)
已知函数f (x)=(x2-1)3+1,求f (x)的极值.
16.已知函数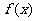 是定义在R上的奇函数,
是定义在R上的奇函数,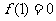 ,
,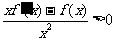
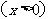 ,则不等式
,则不等式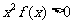 的解集是 .
的解集是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com