
2.设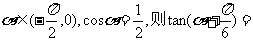 ( )
( )
A.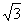 B.
B.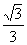 C.-
C.-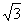 D.-
D.-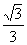
1.设全集U={1,2,3,4,5},集合A={1,2,3},集合B={3,4,5},则(CUA)∪(CUB)=
( )
A.{1,2,3,4,5} B.{3}
C.{1,2,4,5} D.{1,5}
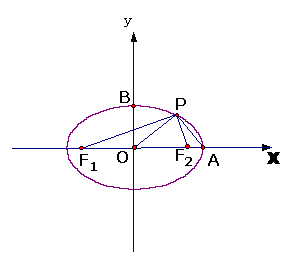
20. (14分)如图,设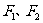 是椭圆
是椭圆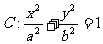 的左右焦点,
的左右焦点,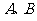 分别是椭圆
分别是椭圆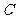 的右顶点和上顶点,
的右顶点和上顶点,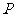 是椭圆
是椭圆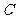 上一点,
上一点,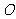 为坐标原点,已知
为坐标原点,已知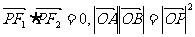 .
.
 (Ⅰ)设椭圆
(Ⅰ)设椭圆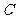 的离心率为
的离心率为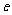 ,证明:
,证明: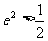 ;
;
(Ⅱ)证明: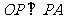 ;
;
(Ⅲ)设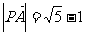 ,求椭圆的长轴长.
,求椭圆的长轴长.
广东省韶关八中2010届高考第二次模拟考试
18. (14分)在M、N两校举行的一次数学解题能力对抗赛中有一道76分的解答题,M校派出选手甲,N校派出选手乙作答。按比赛规则,若该题两选手均未能解出,则每名选手各得0分,若只有一个选手解出,则这个选手得76分,另一名选手得0分;若两选手均解出,则每名选手各得38分.已知甲选手解出这道题的概率是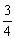 ,乙选手解出这道题的概率是
,乙选手解出这道题的概率是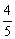 ,且至少有一人能解出该题
,且至少有一人能解出该题
(Ⅰ)求甲选手和乙选手各得38分的概率.
(Ⅱ)分别求出甲选手和乙选手最后得分的数学期望.
(19)(14分)已知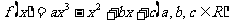 在
在 上是增函数,在[0,3]上是减函数,且方程
上是增函数,在[0,3]上是减函数,且方程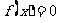 有三个实根,它们分别是
有三个实根,它们分别是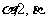 .
.
(Ⅰ)求b的值.并求实数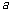 的取值范围.
的取值范围.
(Ⅱ)求证:
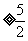
17. (14分)已知正方形ABCD的边长为2,中心为O, 四边形PACE是直角梯形,设 ,且PA=2,CE=1,
,且PA=2,CE=1,
 (Ⅰ)求证PO⊥平面BED
(Ⅰ)求证PO⊥平面BED
(Ⅱ)求二面角E-PB-A的大小.
16. (12分)设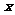 为
为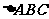 的一个内角,函数
的一个内角,函数
(1)求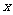 为何值时,
为何值时, 有最大值?并求出该最大值.
有最大值?并求出该最大值.
(Ⅱ)若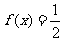 ,求
,求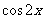 的值。
的值。
15. (12分)已知点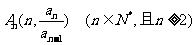 在函数
在函数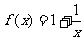 的图像上,且
的图像上,且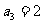 .
.
(Ⅰ)求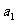
(Ⅱ)求数列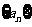 的前
的前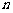 项和.
项和.
14. 已知杨辉三角
1
1 1
1 2 1
1 3 3 1
…………………………
将第4行的第1个数乘以1, 第2个数乘以2, 第3个数乘以4, 第4个数乘以8后,这一行所有数字之和等于
(用数字作答); 若等比数列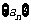 的首项是
的首项是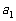 ,公比是
,公比是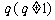 ,将杨辉三角的第
,将杨辉三角的第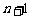 行的第1个数乘以
行的第1个数乘以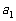 ,第2个数乘以
,第2个数乘以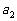 , ,……,第
, ,……,第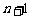 个数乘以
个数乘以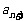 后,这一行的所有数字之和等于
(用
后,这一行的所有数字之和等于
(用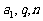 表示)
表示)
13. 正方体ABCD-A1B1C1D1的棱长为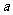 ,E是CC1上的点,当
,E是CC1上的点,当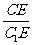 = 时,
= 时,
面A1BD⊥面EBD,此时,三棱锥A1BED的体积= .
12. 已知双曲线C的对称轴为坐标轴,面积是1的等腰直角三角形的一条直角边所在的直线为X轴, 另一条直角边所在的直线为双曲线的一条准线,斜边所在的直线为双曲线的一条渐近线,则双曲线方程为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com