
8.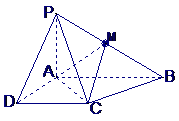 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,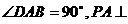 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC=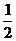 AB=1,M是PB的中点
AB=1,M是PB的中点
(Ⅰ)证明:面PAD⊥面PCD;
(Ⅱ)求AC与PB所成的角;
(Ⅲ)求面AMC与面BMC所成二面角的大小
方法一:
(Ⅰ)证明:∵PA⊥面ABCD,CD⊥AD,
∴由三垂线定理得CD⊥PD.
因而,CD与面PAD内两条相交直线AD,PD都垂直,∴CD⊥面PAD.
 又CD
又CD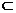 面PCD,∴面PAD⊥面PCD.
面PCD,∴面PAD⊥面PCD.
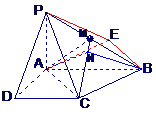
(Ⅱ)解:过点B作BE//CA,且BE=CA,
则∠PBE是AC与PB所成的角.
连结AE,可知AC=CB=BE=AE=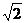 ,又AB=2,
,又AB=2,
所以四边形ACBE为正方形.
由PA⊥面ABCD得∠PEB=90°
在Rt△PEB中BE=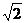 ,PB=
,PB=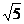 ,
, 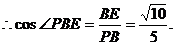

(Ⅲ)解:作AN⊥CM,垂足为N,连结BN.
在Rt△PAB中,AM=MB,又AC=CB, ∴△AMC≌△BMC,
∴BN⊥CM,故∠ANB为所求二面角的平面角
∵CB⊥AC,由三垂线定理,得CB⊥PC,
在Rt△PCB中,CM=MB,所以CM=AM.
在等腰三角形AMC中,AN·MC=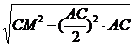 ,
,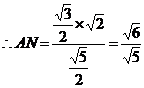
∴AB=2,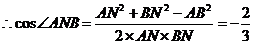 ,故
,故 即为所求.
即为所求.
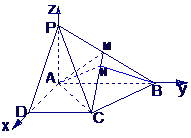
方法二:因为PA⊥PD,PA⊥AB,AD⊥AB,以A为坐标原点AD长为单位长度,如图建立空间直角坐标系,则各点坐标为A(0,0,0)B(0,2,0),C(1,1,0),D(1,0,0),P(0,0,1),M(0,1,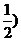 .
.
(Ⅰ)证因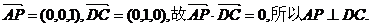
又知AD⊥DC,且AP与与AD是面PAD内的两条相交直线,由此得DC⊥面PAD.
又DC在面PCD上,故面PAD⊥面PCD
 (Ⅱ)解:因
(Ⅱ)解:因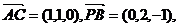
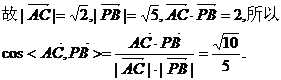
由此得AC与PB所成的角为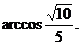
(Ⅲ)解:在MC上取一点N(x,y,z),则存在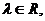 使
使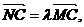
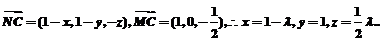
要使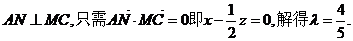
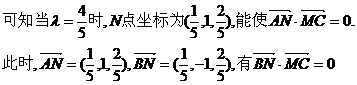
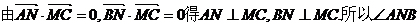 即为所求
即为所求
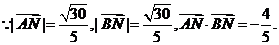
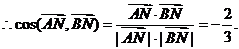

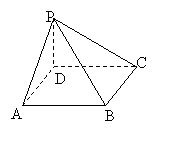
7.在正四面体ABCD中,E、F分别为AD、BC的中点。
(1)求CE与AF所成的角;(2)求直线CE与平面BCD所成的角。
解:(1)连结FD,取FD的中点G,连结GE,∵E、G分别是AD、FD的中点,∴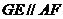 ,故∠CEG(或其补角)即为CE与AF所成的角。设AB=a,在ΔCEG中,
,故∠CEG(或其补角)即为CE与AF所成的角。设AB=a,在ΔCEG中,
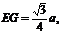
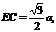
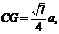
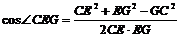
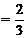
 故CE与AF所成的角为
故CE与AF所成的角为
 。
。
(2)∵正四面体ABCD,∴BC⊥AF,BC⊥DF,
∴BC⊥面AFD,∴面AFD⊥面BCD,过E作EH⊥DF于H,
则EH⊥面BCD,则∠ECH为CE与面BCD所成的角。
在RtΔCEH中,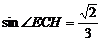 ,
,
即CE与平面BCD成的角为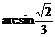 。
。
6.正六棱柱ABCDED-A1B1C1D1E1F1的底面边长为1,侧棱长为,则这个棱柱的侧面对角线E1D与BC1所成的角为 60° 。
5.在△ABC中,M,N分别是AB,AC的中点,PM⊥平面ABC,当BC=18,PM=时,PN和平面ABC所成的角是 30°.
4.已知二面角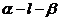 的大小为
的大小为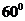 ,
,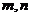 为异面直线,且
为异面直线,且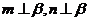 ,则
,则
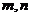 所成的角为( B )
所成的角为( B )
A.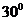 B.
B.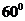 C.
C.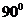 D.
D.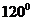
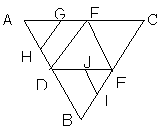
3.如图在正三角形ABC中,E、D、F分别为各边的中
点,G、H、I、J分别为AF、AD、BE、DE的中点,
将三角形沿DE、EF、DF折成三棱锥以后,GH与
IJ所成角的度数为( B )
A.90° B.60° C.45° D.30°
2.如果平面的一条斜线长是它在这个平面上射影长的3倍,那么这条斜线与平面
 所成角的余弦值为( A
)
所成角的余弦值为( A
)
A. B. C. D.
1.平面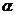 的斜线
的斜线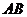 交
交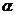 于点
于点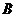 ,过定点
,过定点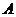 的动直线
的动直线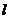 与
与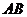 垂直,且交
垂直,且交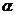 于点
于点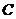 ,则动点
,则动点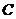 的轨迹是( A )
的轨迹是( A )
(A)一条直线 (B)一个圆 (C)一个椭圆 (D)双曲线的一支
3.二面角的平面角的主要作法:①定义 ②三垂线定义 ③ 垂面法
★★★高考将考什么
[范例1]在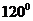 的二面角
的二面角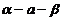 中,
中,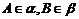 ,已知点A和B到棱的距离分别为2和4,且AB=10。求
,已知点A和B到棱的距离分别为2和4,且AB=10。求
(1)直线AB与棱a所成的角;(2)直线AB与平面β所成的角。
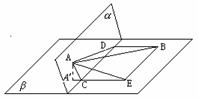 解:(1)如图所示,在平面α内,过A作AC⊥α,垂足为C;在平面β内,过B作BD⊥β,垂足为D;又在平面β内,过B作BE
解:(1)如图所示,在平面α内,过A作AC⊥α,垂足为C;在平面β内,过B作BD⊥β,垂足为D;又在平面β内,过B作BE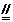 CD,
CD,
连结CE,则∠ABE为AB与α所成的角,CE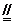 BD,
BD,
从而CE⊥α,∠ACE=1200,∠AEB=900。
在ΔACE中,由余弦定理得
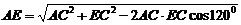
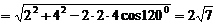
在RtΔAEB中,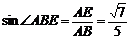 。故直线AB与棱a所成的角为
。故直线AB与棱a所成的角为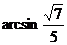
(2)过点A作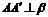 ,则垂足
,则垂足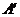 在
在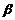 的另一半平面上。
的另一半平面上。
在RtΔAA′C中,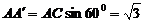 。
。
在RtΔA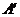 B中,
B中,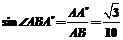 。
。
故直线AB与平面β所成的角为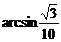
[点晴]本题源于课本,高于课本,不难不繁,体现了通过平移求线线、通过射影求线面角的基本方法。
[文]如右下图,在长方体ABCD-A1B1C1D1中,已知AB= 4, AD =3, AA1= 2.
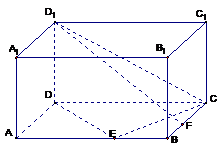 E、F分别是线段AB、BC上的点,且EB= FB=1.
E、F分别是线段AB、BC上的点,且EB= FB=1.
(1) 求二面角C-DE-C1的正切值;
(2) 求直线EC1与FD1所成的余弦值.
解:(I)以A为原点,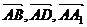 分别为
分别为
x轴,y轴,z轴的正向建立空间直角坐标系,则有
D(0,3,0)、D1(0,3,2)、E(3,0,0)、F(4,1,0)、C1(4,3,2),
故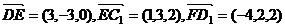
设向量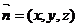 与平面C1DE垂直,则有
与平面C1DE垂直,则有
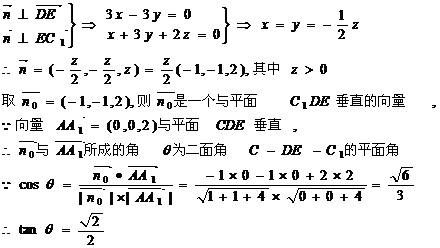
(II)设EC1与FD1所成角为β,则
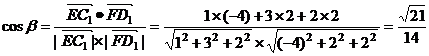 。
。
 [点晴]空间向量在解决含有三维直角的立体几何题中更能体现出它的优点,但必须注意其程序化的过程及计算的公式,本题使用纯几何方法也不难,同学不妨一试。
[点晴]空间向量在解决含有三维直角的立体几何题中更能体现出它的优点,但必须注意其程序化的过程及计算的公式,本题使用纯几何方法也不难,同学不妨一试。
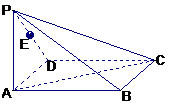
[范例2]如图,在四棱锥P-ABC右,底面ABCD
为矩形,侧棱PA⊥底面ABCD,AB=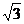 ,BC=1,PA=2,
,BC=1,PA=2,
E为PD的中点
(Ⅰ)求直线AC与PB所成角的余弦值;
(Ⅱ)在侧面PAB内找一点N,使NE⊥面PAC,
并求出N点到AB和AP的距离
解法一:(Ⅰ)建立如图所示的空间直角坐标系,则A、B、C、D、P、E的坐标分别为A(0,0,0),B(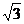 ,0,0),C(
,0,0),C(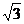 ,1,0),D(0,1,0),P(0,0,2),E(0,
,1,0),D(0,1,0),P(0,0,2),E(0,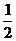 ,2).
,2).
从而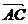 =(
=(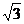 ,1,0),
,1,0),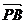 =(
=(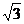 ,0,-2).
,0,-2).
设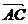 与
与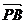 的夹角为
的夹角为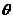 ,则
,则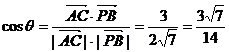 ,
,
∴AC与PB所成角的余弦值为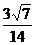

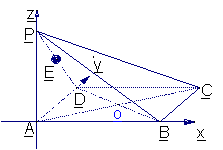 (Ⅱ) N点在侧面PAB内,故可设N点坐标为(x, 0, z),则
(Ⅱ) N点在侧面PAB内,故可设N点坐标为(x, 0, z),则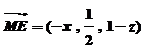
由NE⊥面PAC可得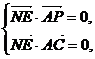
即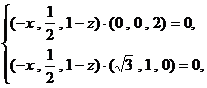
化简得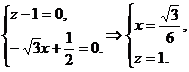
即N点的坐标为(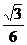 ,0,1),从而N点到AB、AP的距离分别为1,
,0,1),从而N点到AB、AP的距离分别为1,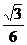

解法二:(Ⅰ)设AC∩BD=O,连OE,则OE//PB,∴∠EOA即为AC与PB所成的角或其补角, 在ΔAOE中,AO=1,OE=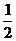 PB=
PB=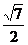 ,AE=
,AE=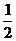 PD=
PD=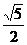 ,
,
∴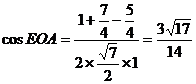 , 即AC与PB所成角的余弦值为
, 即AC与PB所成角的余弦值为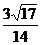
(Ⅱ)在面ABCD内过D作AC的垂线交AB于F,则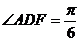 .
.
连PF,则在RtΔADF中DF=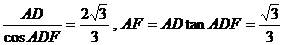 .
.
设N为PF的中点,连NE,则NE//DF,
∵DF⊥AC,DF⊥PA,∴DF⊥面PAC 从而NE⊥面PAC
从而NE⊥面PAC
∴N点到AB的距离=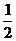 AP=1,N点到AP的距离=
AP=1,N点到AP的距离=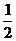 AF=
AF=

[点晴]由线线、线面、面面的位置寻找满足某些条件的点的位置,它能考查学生分析问题、解决问题的能力,两种方法各有优缺点,在向量方法中注意动点的设法,在方法二中注意用分析法寻找思路。
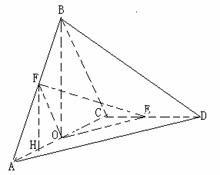 [文]在梯形ABCD中,AB=BC=1,AD=2,
[文]在梯形ABCD中,AB=BC=1,AD=2,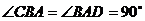 ,沿对角线AC将折起,使点B在平面ACD内的射影O恰在AC上。
,沿对角线AC将折起,使点B在平面ACD内的射影O恰在AC上。
(1)求证:AB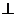 平面BCD
平面BCD
(2)求异面直线BC与AD所成的角。
解:(1)在梯形ABCD中,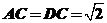 ,AD=2,
,AD=2,
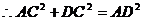 ,
,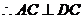
又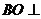 平面ACD,故
平面ACD,故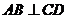
又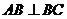 ,且
,且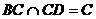
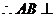 平面BCD
平面BCD
(2)因为BA=BC,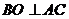 ,
,
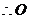 为AC中点,取CD中点E,AB中点F,连结OE、OF、EF,则OE//AD,
为AC中点,取CD中点E,AB中点F,连结OE、OF、EF,则OE//AD,
OF//BC,所以AD与BC所成的角为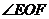 或其补角.
或其补角.
作FH//BO交AC于H,连结HE, 则FH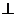 平面ACD
平面ACD
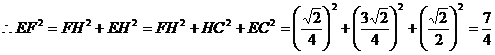
在三角形EOF中,又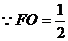 ,EO=1
,EO=1
由余弦定理知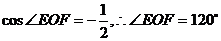
故异面直线BC与AD所成的角为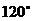
[点晴]折叠问题必须注意折叠前后之间的关系和区别,本题使用空间向量的方法也不失一种好方法。
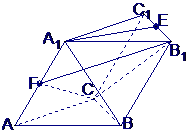
[范例3]如图,在斜三棱柱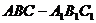 中,
中,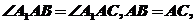
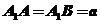 ,侧面
,侧面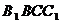 与底面ABC所成的二面角为
与底面ABC所成的二面角为 ,E、F分别是棱
,E、F分别是棱
 的中点
的中点
(Ⅰ)求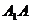 与底面ABC所成的角
与底面ABC所成的角
(Ⅱ)证明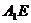 ∥平面
∥平面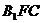
(Ⅲ)求经过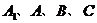 四点的球的体积
四点的球的体积
解:(Ⅰ)过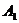 作
作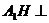 平面
平面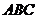 ,垂足为
,垂足为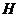
连结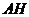 ,并延长交
,并延长交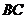 于
于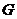 ,
,
于是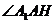 为
为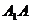 与底面
与底面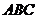 所成的角
所成的角
∵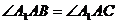 ,∴
,∴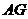 为
为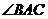 的平分线
的平分线
又∵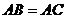 ,∴
,∴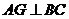 ,且
,且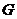 为
为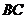 的中点. 由三垂线定理
的中点. 由三垂线定理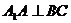 .
.
∵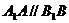 ,且
,且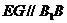 ,∴
,∴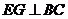 .
.
于是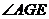 为二面角
为二面角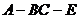 的平面角,即
的平面角,即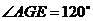 .
.
由于四边形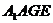 为平行四边形,得
为平行四边形,得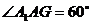 .
.
(Ⅱ)证明:设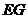 与
与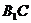 的交点为
的交点为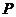 ,则点
,则点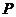 为
为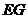 的中点.连结
的中点.连结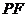 .
.
在平行四边形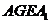 中,因
中,因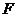 为
为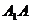 的中点,故
的中点,故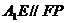 .
.
而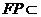 平面
平面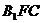 ,
,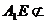 平面
平面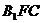 ,所以
,所以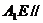 平面
平面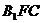 .
.
(Ⅲ)连结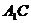 .在
.在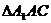 和
和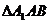 中,由于
中,由于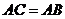 ,
,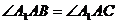 ,
,
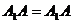 ,则
,则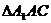 ≌
≌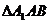 ,故
,故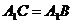 .由已知得
.由已知得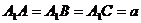
又∵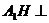 平面
平面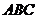 ,∴
,∴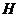 为
为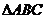 的外心
的外心
设所求球的球心为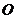 ,则
,则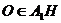 ,且球心
,且球心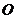 与
与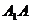 中点的连线
中点的连线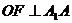
在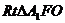 中,
中,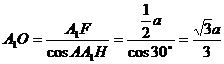 .
.
故所求球的半径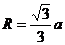 ,球的体积
,球的体积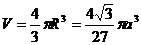 .
.
[点晴](Ⅰ)(Ⅱ)两小题注意使用二面角属于简单立几问题。(Ⅲ)要注意球的几何性质以及平面几何知识的合理利用。
[文]在四棱锥P-ABCD中,ABCD为正方形,PA⊥面ABCD,PA=AB=a,E为BC中点.
(1)求平面PDE与平面PAB所成二面角的大小;
(2)求平面PBA与平面PDC所成二面角的大小
解:(1)延长AB、DE交于点F,则PF为平面PDE与平面PAD所成二面角的棱,
∵PA⊥平面ABCD, ∴AD⊥PA、AB, PA∩AB=A
∴DA⊥平面BPA于A, 过A作AO⊥PF于O,连结OD,
则∠AOD即为平面PDE与平面PAD所成二面角的平面角。
得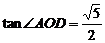 ,故面PDE与面PAD所成二面角的大小为
,故面PDE与面PAD所成二面角的大小为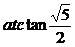
 (2)解法1(面积法)如图∵AD⊥PA、AB,
PA∩AB=A
(2)解法1(面积法)如图∵AD⊥PA、AB,
PA∩AB=A
∴DA⊥平面BPA于A, 同时BC⊥平面BPA于B,
∴△PBA是△PCD在平面PBA上的射影,
设平面PBA与平面PDC所成二面角大小为θ,
cosθ=S△PAB/S△PCD=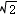 /2
/2 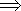 θ=450
θ=450
即平面BAP与平面PDC所成的二面角的大小为45°。
解法2(补形化为定义法)如图将四棱锥P-ABCD补形
得正方体ABCD-PQMN,则PQ⊥PA、PD,于是∠APD是两
面所成二面角的平面角。 在Rt△PAD中,PA=AD,
则∠APD=45°。即平面BAP与平面PDC所成二面角的大小为45°。
[点晴]求线面角、面面角关键在于准确作出角,同样遵循一作二证三计算的步骤,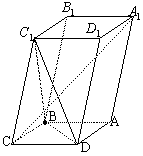 但应用面积射影法求二面角可避免找角,同学们注意经常使用。
但应用面积射影法求二面角可避免找角,同学们注意经常使用。
[范例4]如图,已知平行六面体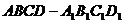 的底
的底
面ABCD是菱形,且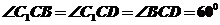 .
.
(I)证明:C1C⊥BD;
(II)假定CD=2,C1C=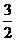 ,记面C1BD为α,面CBD为β,
,记面C1BD为α,面CBD为β,
求二面角α BD β的平面角的余弦值;
(III)当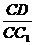 的值为多少时,能使A1C⊥平面C1BD?请给出证明。
的值为多少时,能使A1C⊥平面C1BD?请给出证明。
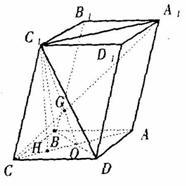 (I)证明:连结
(I)证明:连结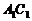 、AC,AC和BD交于O,连结
、AC,AC和BD交于O,连结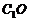 .
.
∵ 四边形ABCD是菱形,∴ AC⊥BD,BC=CD.
又∵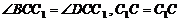 ,
,
∴ 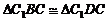 , ∴
, ∴ 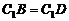 ,
,
∵ DO=OB, ∴ 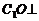 BD,但 AC⊥BD,
BD,但 AC⊥BD,
AC∩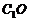 =O, ∴ BD⊥平面
=O, ∴ BD⊥平面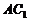 .
.
又 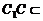 平面
平面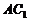 , ∴
, ∴ 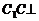 BD.
BD.
(II)解:由(I)知AC⊥BD,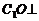 BD,
BD,
∴ 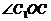 是二面角
是二面角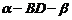 的平面角.
的平面角.
在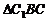 中,BC=2,
中,BC=2,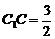 ,
,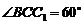 ,
,
∴ 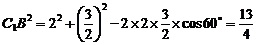 .
.
∵ ∠OCB=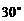 ,∴ OB=
,∴ OB=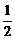 BC=1.∴
BC=1.∴ 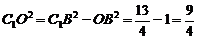 ,
,
∴ 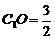 即
即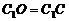 .作
.作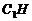 ⊥OC,垂足为H
⊥OC,垂足为H
∴ 点H是OC的中点,且OH 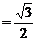 ,所以
,所以 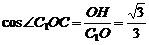 . (III)当
. (III)当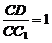 时,能使
时,能使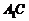 ⊥平面
⊥平面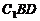 .
.
证法一:∵ 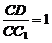 ,∴ BC=CD=
,∴ BC=CD=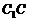 ,又
,又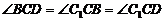 ,
,
由此可推得BD=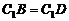 .∴三棱锥C-
.∴三棱锥C- 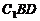 是正三棱锥 设
是正三棱锥 设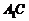 与
与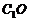 相交于G.∵
相交于G.∵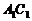 ∥AC,且
∥AC,且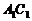 ∶OC=2∶1,∴
∶OC=2∶1,∴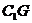 ∶GO=2∶1.
∶GO=2∶1.
又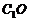 是正三角形
是正三角形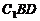 的BD边上的高和中线,
的BD边上的高和中线,
∴点G是正三角形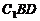 的中心,∴CG⊥平面
的中心,∴CG⊥平面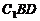 .即
.即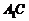 ⊥平面
⊥平面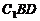
证法二:由(I)知,BD⊥平面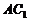 ,∵
,∵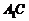
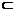 平面
平面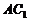 ,∴BD⊥
,∴BD⊥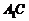 .
.
当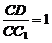 时 ,平行六面体的六个面是全等的菱形,
时 ,平行六面体的六个面是全等的菱形,
同BD⊥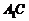 的证法可得
的证法可得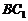 ⊥
⊥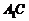 .又 BD∩
.又 BD∩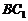 =B,∴
=B,∴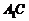 ⊥平面
⊥平面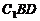 .
.
 [点晴]本题综合考查了立体几何的各种基础知识,(III)作为开放题有一定难度,常使用猜测(或特殊情形猜测)再分析证明的解决方法。
[点晴]本题综合考查了立体几何的各种基础知识,(III)作为开放题有一定难度,常使用猜测(或特殊情形猜测)再分析证明的解决方法。
[文]如图,在四棱锥P-ABCD中,底面ABCD是边长
为a的正方形,并且PD=a,PA=PC=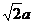 。
。
(1)求证:PD⊥平面ABCD;
(2)求异面直线PB与AC所成的角;
(3)求二面角A-PB-D的大小。
(4)在这个四棱锥中放一个球,求球的最大半径。
解:(1)PC=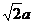 ,PD=PC=a,∴DPDC是RtD,且PD⊥DC,
,PD=PC=a,∴DPDC是RtD,且PD⊥DC,
同理PD⊥AD,又AD∩DC=D, ∴PD⊥平面ABCD。
(2)连BD,因ABCD是正方形,∴BD⊥AC,又PD⊥平面ABCD。
BD是PB在面ABCD上的射影,由三垂线定理得PB⊥AC,∴PB与AC成90°角。
(3)设AC∩BD=O,作AE⊥PB于E,连OE,
∵AC⊥BD,又PD⊥平面ABCD,ACÌ平面ABCD,∴PD⊥AC,
又PD∩BD=D, ∴AC⊥平面PDB,则OE是AE在平面PDB上的射影。
由三垂线定理逆定理知OE⊥PB, ∴ÐAEO是二面角A-PB-D的平面角。
又AB=a,PA=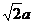 ,PB=
,PB=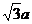 , ∵PD⊥平面ABCD,DA⊥AB,
, ∵PD⊥平面ABCD,DA⊥AB,
∴PA⊥AB,在RtDPAB中,AE•PB=PA•AB。∴AE=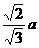 ,又AO=
,又AO=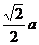
∴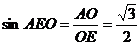 ,ÐAEO=60°,二面角A-PB-D的大小为60°。
,ÐAEO=60°,二面角A-PB-D的大小为60°。
(4)设此球半径为R,最大的球应与四棱锥各个面相切,球心为S,连SA、SB、SC、SD、SP,则把此四棱锥分为五个小四棱锥,它们的高均为R,由体积关系得:
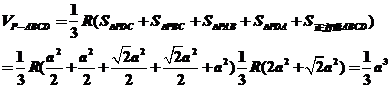
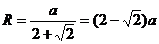 。
。
[点晴]解决(4)的关键是确定球与四棱锥具有怎样的位置关系时,半径最大,此时怎样建立关于球的半径的等量关系式。立体几何中的最值问题,常有两种解决方法:
(1)建立所求量的函数关系式,再求最值;
(2)根据立体几何的有关知识,确定在什么位置时,所求量取最值。
★★★自我提升
2.求角的三个步骤:一猜,二证,三算.猜是关键,在作线面角时,利用空间图形的平行,垂直,对称关系,猜斜线上一点或斜线本身的射影一定落在平面的某个地方,然后再证
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com