
5.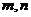 是空间两条不同直线,
是空间两条不同直线,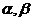 是两个不同平面,下面有四个命题:
是两个不同平面,下面有四个命题:
①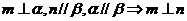 ②
②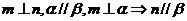
③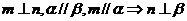 ④
④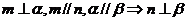
其中真命题的编号是 ①、④ ;(写出所有真命题的编号)
4.在正四面体P-ABC中,D,E,F分别是AB,BC,CA的中点,下面四个结
论中不成立的是(C)
(A)BC//平面PDF (B)DF⊥平面PA E
(C)平面PDF⊥平面ABC (D)平面PAE⊥平面 ABC
3.一平面截一球得到直径是6cm的圆面,球心到这个平
面的距离是4cm,则该球的体积是( C )
(A)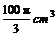 (B)
(B) 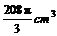 (C)
(C) 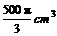 (D)
(D) 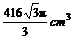
2.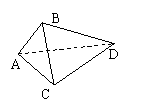 设A、B、C、D是空间四个不同的点,在下列命题中,不正确的 (C)
设A、B、C、D是空间四个不同的点,在下列命题中,不正确的 (C)
(A)若AC与BD共面,则AD与BC共面
(B)若AC与BD是异面直线,则AD与BC是异面直线
(C) 若AB=AC,DB=DC,则AD=BC
(D) 若AB=AC,DB=DC,则AD 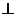 BC
BC
1.设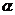 、
、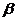 为两个不同的平面,l、m为两条不同的直线,且l
为两个不同的平面,l、m为两条不同的直线,且l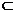
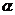 ,m
,m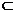
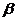 ,有如下的两个命题:①若
,有如下的两个命题:①若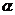 ∥
∥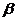 ,则l∥m;②若l⊥m,则
,则l∥m;②若l⊥m,则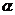 ⊥
⊥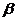 .那么( D )
.那么( D )
(A) ①是真命题,②是假命题 (B) ①是假命题,②是真命题
(C) ①②都是真命题 (D) ①②都是假命题
3.体积法是一种很好的求空间距离的方法.
[范例4]如图,在长方体AC1中,AD=AA1=1,AB=2,点E在棱AB上移动.
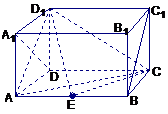 (1)证明:D1E⊥A1D;
(1)证明:D1E⊥A1D;
(2)当E为AB的中点时,求点E到面ACD1的距离;
(3)AE等于何值时,二面角D1-EC-D的大小为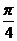 .
.
解析:法1
(1)∵AE⊥面AA1DD1,A1D⊥AD1,∴A1D⊥D1E
(2)设点E到面ACD1的距离为h,在△ACD1中,AC=CD1=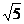 ,AD1=
,AD1=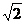 ,
,
故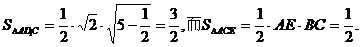
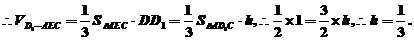
(3)过D作DH⊥CE于H,连D1H、DE,则D1H⊥CE,
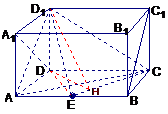 ∴∠DHD1为二面角D1-EC-D的平面角.
∴∠DHD1为二面角D1-EC-D的平面角.
设AE=x,则BE=2-x
法2:以D为坐标原点,直线DA、DC、DD1分别为x、y、z轴,建立空间直角坐标系,设AE=x,则A1(1,0,1),D1(0,0,1),E(1,x,0),A(1,0,0), C(0,2,0).
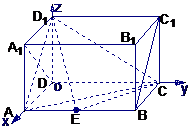 (1)
(1)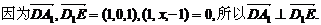
(2)因为E为AB的中点,则E(1,1,0),
从而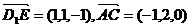 ,
,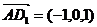 ,
,
设平面ACD1的法向量为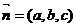 ,
,
则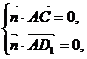 也即
也即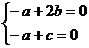 ,得
,得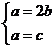 ,
,
从而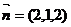 ,所以点E到平面AD1C的距离为
,所以点E到平面AD1C的距离为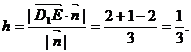
(3)设平面D1EC的法向量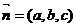 ,
,
∴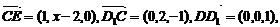
由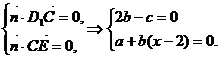 令b=1, ∴c=2, a=2-x,
令b=1, ∴c=2, a=2-x,
∴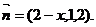 依题意
依题意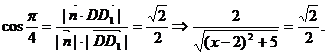
∴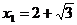 (不合,舍去),
(不合,舍去),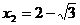 .
.
∴AE=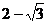 时,二面角D1-EC-D的大小为
时,二面角D1-EC-D的大小为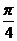 .
.
[点晴]由线线、线面、面面的位置寻找满足某些条件的点的位置,是一种新型题目,它能考查学生分析问题、解决问题的能力,应引起重视,解决这类问题,常用分析法寻找思路。
[文]如图,已知长方体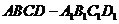
 ,
,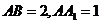 ,直线
,直线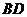 与平
与平
面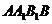 所成的角为
所成的角为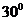 ,
,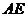 垂直
垂直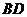 于
于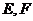 为
为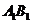 的中点.
的中点.
(Ⅰ)求异面直线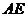 与
与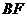 所成的角;
所成的角;
(Ⅱ)求平面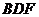 与平面
与平面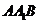 所成二面角(锐角)的大小;
所成二面角(锐角)的大小;
(Ⅲ)求点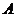 到平面
到平面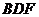 的距离
的距离
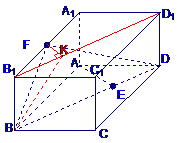 解(Ⅰ)连结
解(Ⅰ)连结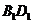 ,过F作
,过F作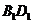 的垂线,垂足为K,
的垂线,垂足为K,
∵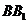 与两底面ABCD,
与两底面ABCD,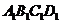 都垂直,
都垂直,
∴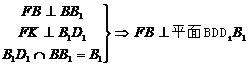
又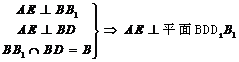
因此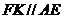
 ∴
∴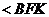 为异面直线
为异面直线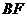 与
与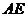 所成的角
所成的角
连结BK,由FK⊥面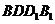 得
得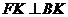 ,从而
,从而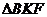 为
为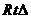

在 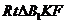 和
和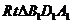 中,
中,
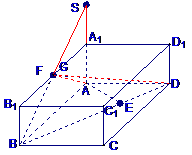 由
由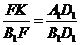 得
得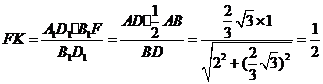

又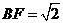 , ∴
, ∴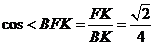

∴异面直线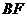 与
与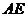 所成的角为
所成的角为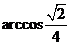

(Ⅱ)由于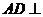 面
面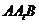 由
由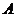 作
作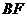 的垂线
的垂线
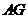 ,垂足为
,垂足为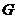 ,连结
,连结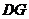 ,则
,则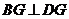

∴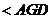 即为平面
即为平面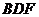 与平面
与平面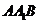 所成二
所成二
面角的平面角。且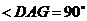 ,在平面
,在平面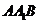 中,延长
中,延长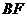 与
与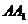 ;交于点
;交于点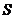 。
。
∵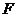 为
为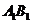 的中点
的中点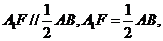
∴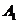 、
、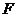 分别为
分别为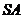 、
、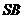 的中点,即
的中点,即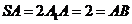 。
。
∴ 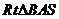 为等腰直角三角形,垂足
为等腰直角三角形,垂足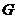 点实为斜边
点实为斜边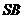 的中点F,即F、G重合。
的中点F,即F、G重合。
易得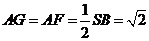 ,在
,在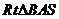 中,
中, 。
。
∴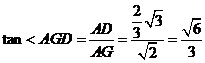 ,∴
,∴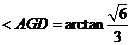 ,
,
即平面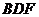 于平面
于平面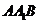 所成二面角(锐角)的大小为
所成二面角(锐角)的大小为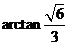 。
。
(Ⅲ)由(Ⅱ)知平面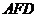 是平面
是平面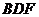 与平面
与平面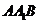 所成二面角的平面角所在的平面
所成二面角的平面角所在的平面
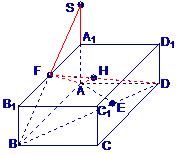 ∴面
∴面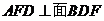
 在
在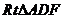 中,由A作
中,由A作
AH⊥DF于H,则AH即为点A到平面BDF的距离.
由AH·DF=AD·AF,得
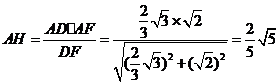
所以点A到平面BDF的距离为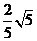
[点晴]本题综合考查了立体几何的知识,异面直线之间的夹角,面面夹角及点与面的距离,考查学生的空间想象能力。
★★★自我提升
2.多用转化的思想求线面和面面距离;
1.常规遵循一作二证三计算的步骤;
2.空间距离则主要是求点到面的距离主要方法:
①体积法; ②直接法,找出点在平面内的射影
★★★高考将考什么
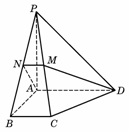
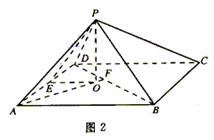
 [范例1]如图,在五面体
[范例1]如图,在五面体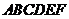 中,点
中,点 是矩形
是矩形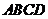 的对角线的交点,面
的对角线的交点,面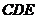 是等边三角形,棱
是等边三角形,棱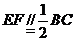 .
.
(1)证明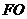 //平面
//平面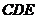 ;
;
|
 (2)设
(2)设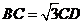 ,
,
证明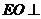 平面
平面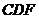 .
.
解析:(Ⅰ)取CD中点M,连结OM.
在矩形ABCD中,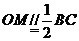 ,又
,又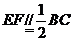 ,则
,则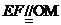 ,
,
连结EM,于是四边形EFOM为平行四边形. 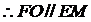
又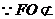 平面CDE, EM
平面CDE, EM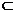 平面CDE, ∴ FO∥平面CDE
平面CDE, ∴ FO∥平面CDE
(Ⅱ)证明:连结FM,由(Ⅰ)和已知条件,在等边△CDE中,
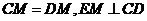 且
且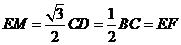 .
.
因此平行四边形EFOM为菱形,从而EO⊥FM而FM∩CD=M,
∴CD⊥平面EOM,从而CD⊥EO. 而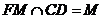 ,所以EO⊥平面CDF.
,所以EO⊥平面CDF.
 [点晴]本小题考查直线与平面平行、直线与平面垂直等基础知识,注意线面平行和线面垂直判定定理的使用,考查空间想象能力和推理论证能力。
[点晴]本小题考查直线与平面平行、直线与平面垂直等基础知识,注意线面平行和线面垂直判定定理的使用,考查空间想象能力和推理论证能力。
[文]如图,在四棱锥P-ABCD中,底面为直角梯形,
AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB
=2BC,M、N分别为PC、PB的中点。
(Ⅰ)求证:PB⊥DM;
(Ⅱ)求CD与平面ADMN所成的角
解析:方法一:
(I)因为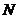 是
是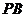 的中点,
的中点,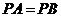 ,所以
,所以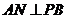 .
.
因为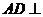 平面
平面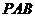 ,所以
,所以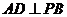 ,从而
,从而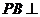 平面
平面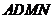 .
.
因为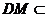 平面
平面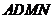 ,所以
,所以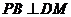 .
.
(II)取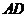 的中点
的中点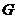 ,连结
,连结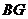 、
、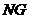 ,则
,则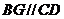 ,
,
所以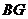 与平面
与平面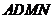 所成的角和
所成的角和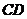 与平面
与平面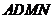 所成的角相等.
所成的角相等.
因为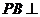 平面
平面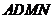 ,所以
,所以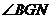 是
是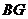 与平面
与平面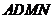 所成的角.
所成的角.
在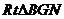 中,
中,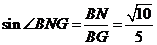 .
.
故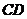 与平面
与平面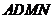 所成的角是
所成的角是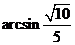 .
.
方法二:
以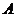 为坐标原点建立空间直角坐标系
为坐标原点建立空间直角坐标系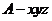 ,设
,设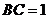 ,则
,则
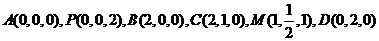 .
.
(I) 因为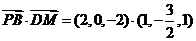
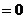 ,所以
,所以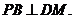
(II) 因为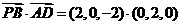
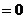 ,所以
,所以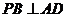 ,
,
又因为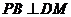 ,所以
,所以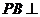 平面
平面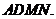
因此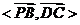 的余角即是
的余角即是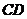 与平面
与平面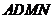 所成的角.
所成的角.
因为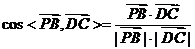
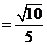 ,
,
所以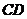 与平面
与平面 所成的角为
所成的角为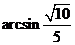 .
.
[点晴]注意线线垂直常使用线面垂直得到解决,线面角关键是找到射影,遵循一作二证三计算的步骤。同时使用空间向量能降低对空间想象能力的要求。
 [范例2]如图,四棱锥P-ABCD中,底面ABCD 为矩形,AB=8,AD=4
[范例2]如图,四棱锥P-ABCD中,底面ABCD 为矩形,AB=8,AD=4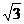 ,侧面PAD为等边三角形,并且与底面所成二面角为60°.
,侧面PAD为等边三角形,并且与底面所成二面角为60°.
(Ⅰ)求四棱锥P-ABCD的体积;
(Ⅱ)证明PA⊥BD.
解析:(Ⅰ)如图,取AD的中点E,
连结PE,则PE⊥AD.
作PO⊥平面在ABCD,垂足为O,连结OE.
根据三垂线定理的逆定理得OE⊥AD,
所以∠PEO为侧面PAD与底面所成的二面角
的平面角,由已知条件可知∠PEO=60°,PE=6,所以PO=3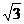 ,
,
四棱锥P-ABCD的体积VP-ABCD=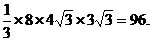
(Ⅱ)法1 如图,以O为原点建立空间直角坐标系.通过计算可得P(0,0,3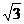 ),
),
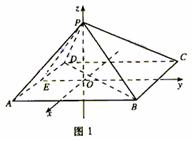 A(2
A(2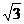 ,-3,0),B(2
,-3,0),B(2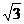 ,5,0),D(-2
,5,0),D(-2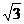 ,-3,0)
,-3,0)
所以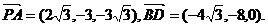
因为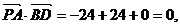 所以PA⊥BD.
所以PA⊥BD.
法2:连结AO,延长AO交BD于点F.通过计算
可得EO=3,AE=2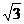 ,又知AD=4
,又知AD=4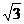 ,AB=8,
,AB=8,
得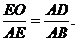 所以Rt△AEO∽Rt△BAD.得∠EAO=∠ABD.
所以Rt△AEO∽Rt△BAD.得∠EAO=∠ABD.
所以∠EAO+∠ADF=90° 所以 AF⊥BD.
因为 直线AF为直线PA在平面ABCD 内的身影,所以PA⊥BD.
[点晴]本小题主要考查棱锥的体积、二面角、异面直线所成的角等知识和空间想象能力、分析问题能力,解题的关键是二面角的使用。使用空间向量能降低对空间想象能力的要求,但坐标系的位置不规则,注意点坐标的表示。
[文]在直三棱柱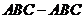 中,
中,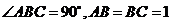 .
.
(1)求异面直线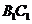 与
与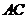 所成的角的大小;
所成的角的大小;
(2)若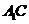 与平面
与平面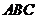 所成角为
所成角为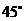 ,求三棱锥
,求三棱锥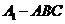 的体积。
的体积。
解析 (1) ∵ BC∥B1C1, ∴∠ACB为异面直线B1C1与AC所成角(或它的补角)
∵∠ABC=90°, AB=BC=1, ∴∠ACB=45°,
∴ 异面直线B1C1与AC所成角为45°.
(2) ∵ AA1⊥平面ABC,∠ACA1是A1C与平面ABC所成的角, ∠ACA =45°.
∵ ∠ABC=90°,
AB=BC=1, AC=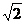 ,∴AA1=
,∴AA1=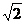 .
.
∴ 三棱锥A1-ABC的体积V=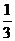 S△ABC×AA1=
S△ABC×AA1=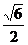 .
.
[点晴]画图是学好立体几何的基本要求,本题考查了线线角和体积等立几知识。
[范例3]如图,所示的多面体是由底面为ABCD的长方体被截面AEC1F所截面而得到的,其中AB=4,BC=2,CC1=3,BE=1.
(Ⅰ)求BF的长;
(Ⅱ)求点C到平面AEC1F的距离.
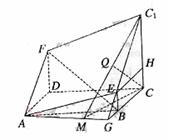 解法1:(Ⅰ)过E作EH//BC交CC1于H,则CH=BE=1,EH//AD,且EH=AD.
解法1:(Ⅰ)过E作EH//BC交CC1于H,则CH=BE=1,EH//AD,且EH=AD.
∵AF∥EC1,∴∠FAD=∠C1EH. ∴Rt△ADF≌Rt△EHC1.
∴DF=C1H=2. 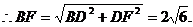
(Ⅱ)延长C1E与CB交于G,连AG,
则平面AEC1F与平面ABCD相交于AG.
过C作CM⊥AG,垂足为M,连C1M,
由三垂线定理可知AG⊥C1M.由于AG⊥面C1MC,
且AG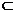 面AEC1F,所以平面AEC1F⊥面C1MC.
面AEC1F,所以平面AEC1F⊥面C1MC.
在Rt△C1CM中,作CQ⊥MC1,垂足为Q,则CQ的长即为C到面AEC1F的距离.
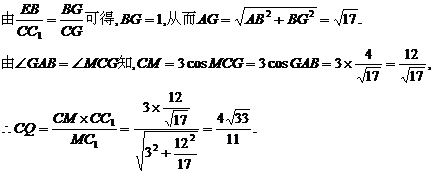
解法2:(I)建立如图所示的空间直角坐标系,则D(0,0,0),B(2,4,0),
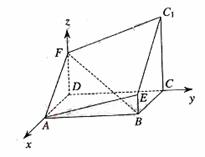 A(2,0,0),C(0,4,0),E(2,4,1),C1(0,4,3).设F(0,0,z).
A(2,0,0),C(0,4,0),E(2,4,1),C1(0,4,3).设F(0,0,z).
∵AEC1F为平行四边形,
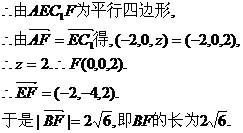
(II)设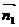 为面AEC1F的法向量,
为面AEC1F的法向量,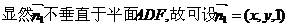
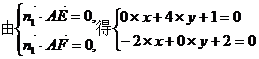
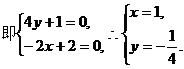
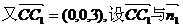 的夹角为a,则
的夹角为a,则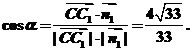
∴C到平面AEC1F的距离为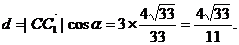
[点晴]本小题主要考查线面关系和空间距离的求法等基础知识,空间距离也遵循一作二证三计算的步骤,但体积法是一种很好的求空间距离的方法,同学们不妨一试。
[文]正三棱柱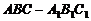 的底面边长为8,对角线
的底面边长为8,对角线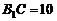 ,D是AC的中点。
,D是AC的中点。
(1)求点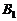 到直线AC的距离.
到直线AC的距离.
(2)求直线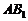 到平面
到平面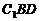 的距离.
的距离.
解:(1)连结BD,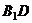 ,由三垂线
,由三垂线 定理可得:
定理可得: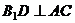 ,
,
所以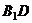 就是
就是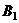 点到直线AC的距离。
点到直线AC的距离。
 在
在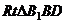 中
中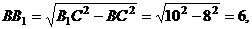
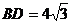 .
.
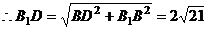 .
.
(2)因为AC与平面BD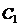 交于AC的中点D,
交于AC的中点D,
设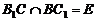 ,则
,则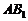 //DE,所以
//DE,所以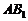 //平面
//平面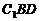 ,
,
所以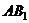 到平面BD
到平面BD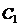 的距离等于A点到平面BD
的距离等于A点到平面BD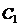
的距离,等于C点到平面BD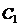 的距离,也就等于三棱
的距离,也就等于三棱
锥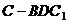 的高,
的高,
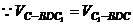 ,
,
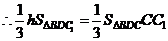 ,
,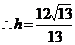 ,即直线
,即直线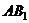 到平面BD
到平面BD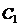 的距离是
的距离是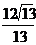 .
.
[点晴]求空间距离注意三点:
1. 转化思想:
① 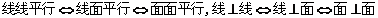 ;
;
② 异面直线间的距离转化为平行线面之间的距离,
平行线面、平行面面之间的距离转化为点与面的距离。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com