
★★★突破重难点
[范例1]已知P是直线3x+4y+8=0上的动点,PA、PB是圆 x2+y2-2x-2y+1=0的两条切线,A、B是切点,C是圆心,求四边形PACB面积的最小值.
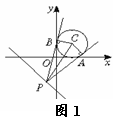 解法一:∵点P在直线3x+4y+8=0上. 如图1.
解法一:∵点P在直线3x+4y+8=0上. 如图1.
∴设P(x,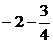 x),C点坐标为(1,1),
x),C点坐标为(1,1),
S四边形PACB=2S△PAC=|AP|·|AC|=|AP|·|AC|=|AP|
∵|AP|2=|PC|2-|AC|2=|PC|2-1
∴当|PC|最小时,|AP|最小,四边形PACB的面积最小.
∴|PC|2=(1-x)2+(1+2+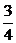 x)2=
x)2=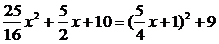
∴|PC|min=3 ∴四边形PACB面积的最小值为2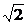 .
.
解法二:由法一知需求|PC|最小值,即求C到直线3x+4y+8=0的距离,∵C(1,1),∴|PC|=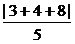 =3,SPACD=2
=3,SPACD=2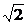 .
.
[点晴]求角、距离、面积等几何量问题的关键在于分析几何问题的特殊性,寻找快捷简便的方法。本题的关键在于S四边形PACB=2S△PAC,然而转化为|PC|的最值问题。
[文]已知等腰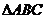 的底边AB所在的直线方程为
的底边AB所在的直线方程为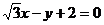 ,顶点C的坐标是(2,2),顶角为1200,求两腰所在的直线方程及
,顶点C的坐标是(2,2),顶角为1200,求两腰所在的直线方程及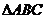 的面积.
的面积.
解:设腰所在直线的斜率为k,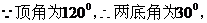
又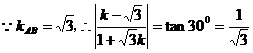 ,
,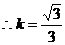 ,
,
故一腰所在直线方程为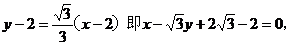
另一腰垂直于x轴,方程为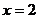 .S
.S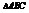 =
=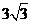
[范例2]过点M(2,4)作两条互相垂直的直线,分别交x、y的正半轴于A、B,若四边形OAMB的面积被直线AB平分,求直线AB方程。
解:设AB的方程为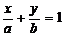 (a>0,b>0)
(a>0,b>0)
∴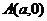 、
、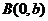 。 ∵
。 ∵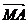 ⊥
⊥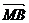
∴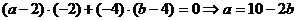
∵a>0 0<b<5 ∵AB方程的一般式为bx+ay-ab=0
∴M到AB的距离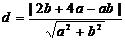
∴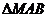 的面积
的面积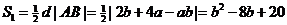
而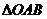 的面积
的面积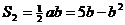 ,
,
∵直线AB平分四边形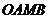 的面积,∴
的面积,∴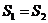 ,
,
可得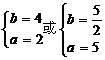
故所求AB方程为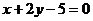 和
和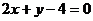 。
。
[点晴]若命题中的直线与两坐标轴均有交点,应先考虑选用截距式方程是否有利。
[文]已知点P到两个定点M(-1,0)、N(1,0)距离的比为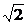 ,点N到直线PM的距离为1.求直线PN的方程
,点N到直线PM的距离为1.求直线PN的方程
解:设点P的坐标为(x,y),由题设有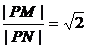 ,
,
即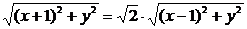 .
.
整理得 x2+y2-6x+1=0. ①
因为点N到PM的距离为1,|MN|=2,
所以∠PMN=30°,直线PM的斜率为±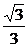 ,
,
直线PM的方程为y=±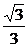 (x+1).②
(x+1).②
将②式代入①式整理得x2-4x+1=0.解得x=2+ ,x=2-
,x=2- .
.
代入②式得点P的坐标为(2+ ,1+
,1+ )或(2-
)或(2- ,-1+
,-1+ );
);
(2+ ,-1-
,-1- )或(2-
)或(2- ,1-
,1- ).
).
直线PN的方程为y=x-1或y=-x+1.
[范例3] 已知气象台A处向西300km处,有个台风中心,已知台风以每小时40km的速度向东北方向移动,距台风中心250km以内的地方都处在台风圈内,问:从现在起,大约多长时间后,气象台A处进入台风圈?气象台A处在台风圈内的时间大约多长?
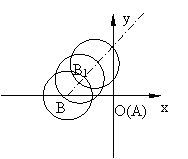 解:如图建立直角坐标系,B为台风中心,处在台
解:如图建立直角坐标系,B为台风中心,处在台
风圈内的界线为以B为圆心,半径为250的圈内,若t
小时后,台风中心到达B1点,
则B1(-300+40tCOS450,40tsin450),
则以B1为圆心,250为半径的圆的方程为
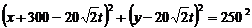
那么台风圈内的点就应满足
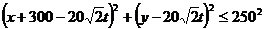 。
。
若气象台A处进入台风圈,那么A点的坐标就应满足上述关系式,把A点的坐标(0,0)代入上面不等式,
得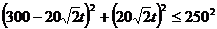 ,解得
,解得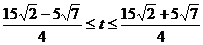 ,
,
即为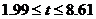 ;
;
所以气象台A处约在2小时后进入台风圈,处在台风圈内的时间大约6小时37分。
[点晴]做应用题的关键是寻求有效信息,建立数量之间的关系。
[文]设A(-c,0),B(c,0)(c>0)为两定点,动点P到A点的距离与到B点的距离的比为定值a(a>0),求P点的轨迹.
解:设动点P的坐标为P(x,y),由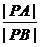 =a(a>0)得
=a(a>0)得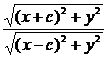 =a,
=a,
化简得(1-a2)x2+2c(1+a2)x+c2(1-a2)+(1-a2)y2=0.
当a≠1时,得x2+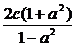 x+c2+y2=0. 整理得(x-
x+c2+y2=0. 整理得(x-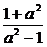 c) 2+y2=(
c) 2+y2=(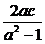 )2
)2
当a=1时,化简得x=0.
所以当a≠1时,P点的轨迹是以(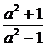 c,0)为圆心,|
c,0)为圆心,|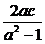 |为半径的圆;
|为半径的圆;
当a=1时,P点的轨迹为y轴.
[点睛]本题考查直线、圆、曲线和方程等基本知识,考查运用解析几何的方法解决问题的能力.
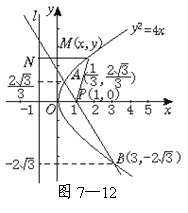
[范例4]已知动圆过定点P(1,0),且与定直线l:x=-1相切,点C在l上.
(Ⅰ)求动圆圆心的轨迹M的方程;
(Ⅱ)设过点P,且斜率为- 的直线与曲线M相交于A、B两点.
的直线与曲线M相交于A、B两点.
(i)问:△ABC能否为正三角形?若能,求点C的坐标;若不能,说明理由;
(ii)当△ABC为钝角三角形时,求这种点C的纵坐标的取值范围.
(Ⅰ)法1 依题意,曲线M是以点P为焦点,直线l为准线的抛物线,
所以曲线M的方程为y2=4x.
法2 设M(x,y),依题意有|MP|=|MN|,
所以|x+1|=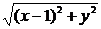 .化简得:y2=4x.
.化简得:y2=4x.
(Ⅱ)(i)由题意得,直线AB的方程为y=- (x-1).
(x-1).
 由
由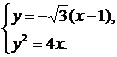 消y得3x2-10x+3=0,
消y得3x2-10x+3=0,
解得x1=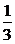 ,x2=3.
,x2=3.
所以A点坐标为(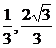 ),
),
B点坐标为(3,-2 ),
),
|AB|=x1+x2+2=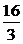 .
.
假设存在点C(-1,y),使△ABC为正三角形,则|BC|=|AB|且|AC|=|AB|,
|
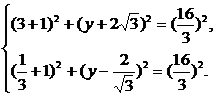
由①-②得42+(y+2 )2=(
)2=(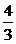 )2+(y-
)2+(y-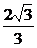 )2,
)2,
解得y=-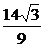 . 但y=-
. 但y=-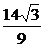 不符合①,
不符合①,
所以由①,②组成的方程组无解.
因此,直线l上不存在点C,使得△ABC是正三角形.
(ii)法1:设C(-1,y)使△ABC成钝角三角形,由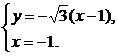
得y=2 ,即当点C(-1,2
,即当点C(-1,2 )时,A、B、C三点共线,故y≠2
)时,A、B、C三点共线,故y≠2 .
.
又|AC|2=(-1-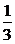 )2+(y-
)2+(y-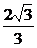 )2=
)2=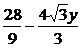 +y2,
+y2,
|BC|2=(3+1)2+(y+2 )2=28+4
)2=28+4 y+y2,|AB|2=(
y+y2,|AB|2=(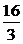 )2=
)2=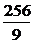 .
.
当∠CAB为钝角时,cosA=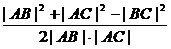 <0.
<0.
即|BC|2
>|AC|2+|AB|2,即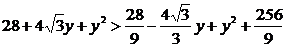 ,
,
即y>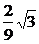 时,∠CAB为钝角.
时,∠CAB为钝角.
当|AC|2>|BC|2+|AB|2,即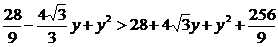 ,
,
即y<-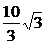 时,∠CBA为钝角.
时,∠CBA为钝角.
又|AB|2>|AC|2+|BC|2,即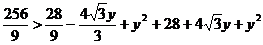 ,
,
即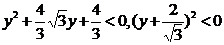 .
.
该不等式无解,所以∠ACB不可能为钝角.
因此,当△ABC为钝角三角形时,点C的纵坐标y的取值范围是
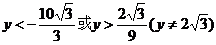 .
.
法2:以AB为直径的圆的方程为(x-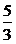 )2+(y+
)2+(y+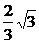 )2=(
)2=(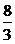 )2.
)2.
圆心(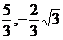 )到直线l:x=-1的距离为
)到直线l:x=-1的距离为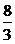 ,
,
所以,以AB为直径的圆与直线l相切于点G(-1,-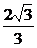 ).
).
当直线l上的C点与G重合时,∠ACB为直角,当C与G点不重合,且A、B、C三点不共线时,∠ACB为锐角,即△ABC中,∠ACB不可能是钝角.
因此,要使△ABC为钝角三角形,只可能是∠CAB或∠CBA为钝角.
过点A且与AB垂直的直线方程为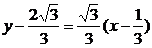 .令x=-1得y=
.令x=-1得y=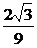 .
.
过点B且与AB垂直的直线方程为y+2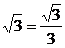 ( x-3).令x=-1得y=-
( x-3).令x=-1得y=-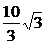 .
.
又由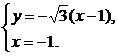 解得y=2
解得y=2 ,
,
所以,当点C的坐标为(-1,2 )时,A、B、C三点共线,不构成三角形.
)时,A、B、C三点共线,不构成三角形.
因此,当△ABC为钝角三角形时,点C的纵坐标y的取值范围是
y<-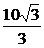 或y>
或y>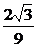 (y≠2
(y≠2 ).
).
[点晴]该题全面综合了解析几何、平面几何、代数的相关知识,充分体现了“注重学科知识的内在联系”.题目的设计新颖脱俗,能较好地考查考生综合运用数学知识解决问题的能力.比较深刻地考查了解析法的原理和应用,以及分类讨论的思想、方程的思想.该题对思维的目的性、逻辑性、周密性、灵活性都进行了不同程度的考查.对运算、化简能力要求也较高,有较好的区分度.
[文]设圆满足:①截y轴所得弦长为2;②被x轴分成两段圆弧,其弧长的比为3:1;③圆心到直线l:x-2y=0的距离为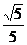 。求该圆的方程。
。求该圆的方程。
解:设圆的圆心为P(a,b),半径为r,则点P到x轴,y轴距离分别为|b|,|a|
由题设知圆P截x轴所得劣弧对的圆心角为900,
知圆P截x轴所得的弦长为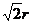 ,故r2=2b2
,故r2=2b2
又圆P截y轴所得的弦长为2,所以有r2=a2+1从而得2b2-a2=1
又点P(a,b)到直线x-2y=0的距离为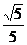 ,所以
,所以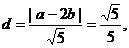
即有a-2b=±1,由此有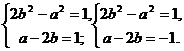
解方程组得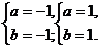 于是r2=2b2知
于是r2=2b2知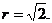
所求圆的方程是(x-1)2+(y-1)2=2或(x+1)2+(y+1)2=2
★★★自我提升
1.将直线l沿x轴正方向平移两个单位,再沿y轴负方向平移3个单位,又回到了原来的位置,则l的斜率为( B )
A. 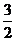 B.
B.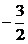 C.
C.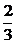 D.
D.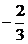
(1)与直线方程特征值(主要指斜率、截距)有关的问题;
(2)直线的平行和垂直的条件;
(3)与距离有关的问题等。
此类题大都属于中、低档题,以选择题和填空题形式出现;
8.已知函数f(x)=x3-x2+ + , 且存在x0∈(0, ) ,使f(x0)=x0.
(I)证明:f(x)是R上的单调增函数;
(II)设x1=0, xn+1=f(xn);y1=, yn+1=f(yn), 其中 n=1,2,…,
证明:xn<xn+1<x0<yn+1<yn;
(III)证明: <
解: (I)∵f '(x)=3x2-2x+ = 3(x-)2+ >0 , ∴f(x)是R上的单调增函数.
(II)∵0<x0< , 即x1<x0<y1.又f(x)是增函数, ∴f(x1)<f(x0)<f(y1).即x2<x0<y2.
又x2=f(x1)=f(0)=>0 =x1, y2=f(y1)=f()=<=y1,综上, x1<x2<x0<y2<y1.
用数学归纳法证明如下:
(1)当n=1时,上面已证明成立.
(2)假设当n=k(k≥1)时有xk<xk+1<x0<yk+1<yk .
当n=k+1时,由f(x)是单调增函数,有f(xk)<f(xk+1)<f(x0)<f(yk+1)<f(yk),
∴xk+1<xk+2<x0<yk+2<yk+1
由(1)(2)知对一切n=1,2,…,都有xn<xn+1<x0<yn+1<yn.
(III) = = yn2+xnyn+xn2-(yn+xn)+ ≤(yn+xn)2-(yn+xn)+
=[(yn+xn)-]2+ . 由(Ⅱ)知 0<yn+xn<1.∴- < yn+xn- < ,
∴ < ()2+ =
[文]已知集合A=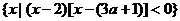 ,B=
,B=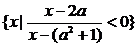 .
.
(1)当a=2时,求A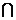 B;
(2)求使B
B;
(2)求使B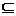 A的实数a的取值范围.
A的实数a的取值范围.
解:(1)当a=2时,A=(2,7),B=(4,5)∴ A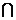 B=(4,5).
B=(4,5).
(2)∵ B=(2a,a2+1),当a<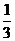 时,A=(3a+1,2)
时,A=(3a+1,2)
要使B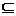 A,必须
A,必须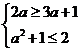 ,此时a=-1;
,此时a=-1;
当a=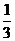 时,A=
时,A=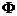 ,使B
,使B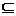 A的a不存在;
A的a不存在;
当a>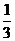 时,A=(2,3a+1)要使B
时,A=(2,3a+1)要使B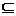 A,必须
A,必须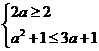 ,此时1≤a≤3.
,此时1≤a≤3.
综上可知,使B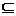 A的实数a的取值范围为[1,3]∪{-1}
A的实数a的取值范围为[1,3]∪{-1}
2.“a>b>0”是“ab<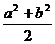 ”的( A )
”的( A )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不允分也不必要条件
3.设f(x)=
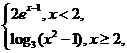
 则不等式f(x)>2的解集为( C )
则不等式f(x)>2的解集为( C )
A.(1,2)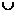 (3,+∞) B.(
(3,+∞) B.(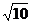 ,+∞)
,+∞)
C.(1,2)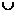 (
(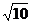 ,+∞) D.(1,2)
,+∞) D.(1,2)
4.若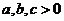 且
且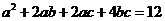 ,则
,则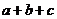 的最小值是( A
)
的最小值是( A
)
A.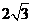 B.3 C.2 D.
B.3 C.2 D.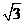
5.不等式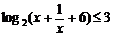 的解集为 .
的解集为 . 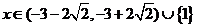
6.三个同学对问题“关于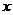 的不等式
的不等式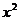 +25+|
+25+|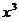 -5
-5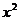 |≥
|≥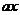 在[1,12]上恒成立,求实数
在[1,12]上恒成立,求实数 的取值范围”提出各自的解题思路.
的取值范围”提出各自的解题思路.
甲说:“只须不等式左边的最小值不小于右边的最大值”.
乙说:“把不等式变形为左边含变量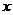 的函数,右边仅含常数,求函数的最值”.
的函数,右边仅含常数,求函数的最值”.
丙说:“把不等式两边看成关于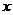 的函数,作出函数图像”.
的函数,作出函数图像”.
参考上述解题思路,你认为他们所讨论的问题的正确结论,即 的取值范围是
的取值范围是
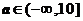
7.已知椭圆C1的方程为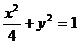 ,双曲线C2的左、右焦点分别为C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点。
,双曲线C2的左、右焦点分别为C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点。
(1) 求双曲线C2的方程;
(2) 若直线l: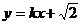 与椭圆C1及双曲线C2恒有两个不同的交点,且l与C2的两个交点A和B满足
与椭圆C1及双曲线C2恒有两个不同的交点,且l与C2的两个交点A和B满足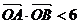 (其中O为原点),求k的取值范围。
(其中O为原点),求k的取值范围。
解:(Ⅰ)设双曲线C2的方程为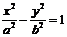 ,则
,则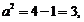
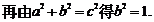 故C2的方程为
故C2的方程为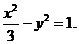
(II)将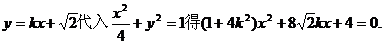
由直线l与椭圆C1恒有两个不同的交点得
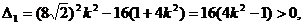 即
即 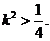 ①
①
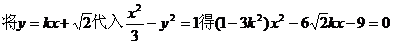 .
.
由直线l与双曲线C2恒有两个不同的交点A,B得
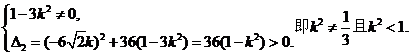
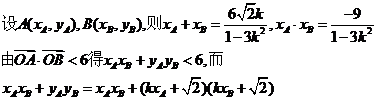
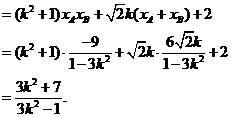
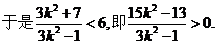 解此不等式得
解此不等式得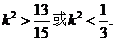 ③
③
由①、②、③得
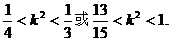
故k的取值范围为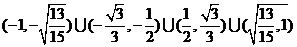
[文]二次函数f(x)满足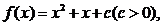 若f(x)= 0有两个实数根
若f(x)= 0有两个实数根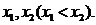
(1)求正数c的取值范围;
(2)求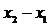 的取值范围.
的取值范围.
解:(1)∵f(x)=0有两个不等实数根
∴△>0 即1-4C>0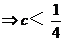 ∴
∴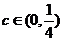
(2)∵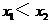 故
故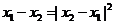 =
=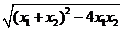 =
=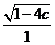
∵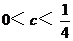 ∴
∴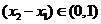 .
.
1.如果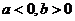 ,那么,下列不等式中正确的是( A
)
,那么,下列不等式中正确的是( A
)
A.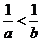 B.
B.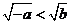 C.
C.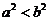 D.
D.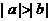
3.已知函数f(x)=ax2+2ax+4(a>0),若x1<x2 , x1+x2=0 , 则( A )
A.f(x1)<f(x2) B.f(x1)=f(x2) C.f(x1)>f(x2) D.f(x1)与f(x2)的大小不能确定
4.不等式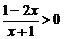 的解集是
的解集是 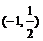 .
.
5.已知直线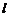 过点
过点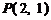 ,且与
,且与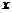 轴、
轴、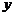 轴的正半轴分别交于
轴的正半轴分别交于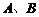 两点,
两点,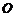 为坐标原点,则三角形
为坐标原点,则三角形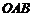 面积的最小值为 . 4
面积的最小值为 . 4
6.如图,已知椭圆的中心在坐标原点,焦点F1,F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,|MA1|∶|A1F1|=2∶1.
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线l1:x=m(|m|>1),P为l1上的动点,使∠F1PF2最大的点P记为Q,求点Q的坐标(用m表示).
[专家解答](I)设椭圆方程为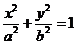 (
(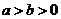 ),半焦距为c, 则
),半焦距为c, 则

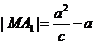 ,
,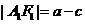 ,
,
由题意,得 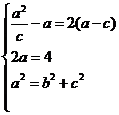 ,
,
解得 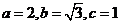
故椭圆方程为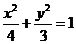
(II)设P(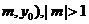 , 当
, 当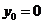 时,
时,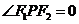
当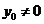 时,
时, 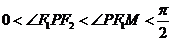
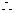 只需求
只需求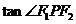 的最大值即可。
的最大值即可。
直线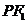 的斜率
的斜率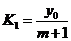 ,直线
,直线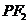 的斜率
的斜率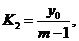
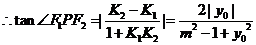
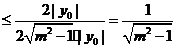
当且仅当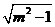 =
=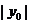 时,
时,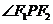 最大,
最大,
★★★高考要考什么
[考点透视]
本专题主要涉及不等式的性质;两个正数的算术平均数不小于它们的几何平均数;比较法、分析法、综合法、反证法、换元法、判别式法、放缩法等证明不等式;二次不等式、绝对值不等式、分式不等式、高次不等式等简单不等式的解法;不等式的应用.
[热点透析]
本专题热点主要体现在解含参数的分式不等式和绝对值不等式;不等式在函数、数列、导数、解析几何、三角函数等的广泛运用.
★★★突破重难点
[范例1]已知a、b、c为不等正数,且abc=1,求证: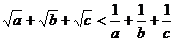
证法一:∵a、b、c为不等正数,且abc=1,
∴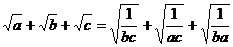
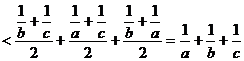
证法二:∵a、b、c为不等正数,且abc=1,
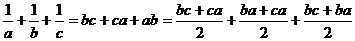
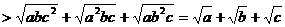
[点晴]证明本题应灵活运用条件abc=1。
[文]解关于x的不等式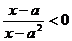 (
(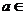 R).
R).
解: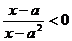
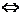 (x-
(x- )(x-
)(x-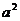 )<0
)<0
(1) 若 =0则
=0则 =
=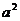 =0,不等式变为 x2<0,解集为φ;
=0,不等式变为 x2<0,解集为φ;
(2) 若 =1则
=1则 =
=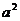 =1 不等式变为
=1 不等式变为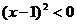 ,解集为φ;
,解集为φ;
(3) 当0< <1时,
<1时, >
>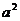 故解集为{x|
故解集为{x|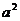 <x<
<x< };
};
(4) 当 <0或
<0或 >1时,
>1时,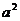 >
> 故解集为{x|
故解集为{x| <x<
<x<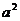 };
};
综上得:当 =0或
=0或 =1时解集为φ;
=1时解集为φ;
当0< <1时,解集为{x|
<1时,解集为{x|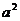 <x<
<x< };
};
当 <0或
<0或 >1时,解集为{x|
>1时,解集为{x| <x<
<x<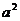 };
};
[点晴]解各种不等式的基本思路是应用合适的性质把原不等式转化为整式不等式,再经过因式分解,用零点划分区间法求解,还应注意对不等式中字母进行分类讨论
[范例2]例5、设a1、a2∈R+, a1+a2=1, λ1、λ2∈R+,
求证: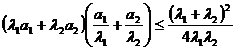
证明:(法1):左边=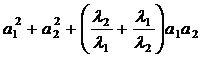
=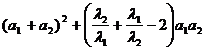 =1+
=1+ 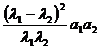
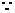 a1、a2∈R+, a1+a2=1,
a1、a2∈R+, a1+a2=1,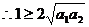 ,
, 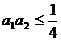 又
又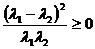
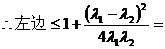
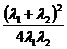
(法2)左=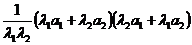
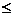
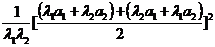
=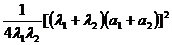 =右边
=右边
[点晴]原不等式从左边到右边如何消去a1,a2,要产生a1+a2.
[文]已知正数x,y满足x+2y=1,求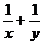 的最小值。
的最小值。
解: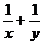
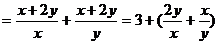
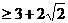 ,
,
当且仅当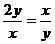 解得
解得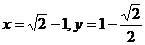 时取等号,
时取等号,
故所求最小值为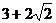 。
。
[点睛]将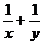 中的1用x+2y进行代换,然后求
中的1用x+2y进行代换,然后求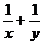 的最小值,在使用基本不等式时一定要注意“一正,二定,三相等”。
的最小值,在使用基本不等式时一定要注意“一正,二定,三相等”。
[范例3]设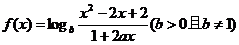 ,
,
(1)求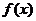 的定义域;
的定义域;
(2)当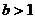 时,解不等式
时,解不等式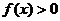 。
。
解:(1)由于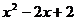 恒正,故所求定义域由
恒正,故所求定义域由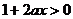 确定,
确定,
① 当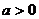 时,定义域为
时,定义域为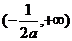 ;
;
② 当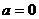 时,定义域为R;
时,定义域为R;
③ 当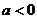 时,定义域为
时,定义域为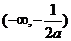 。
。
(2)当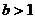 时,
时,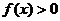
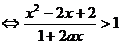
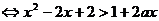
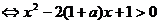 ,其判别式
,其判别式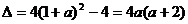
①当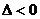 即
即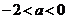 时,
时,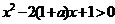 恒成立,所求解集为
恒成立,所求解集为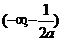 ;
;
②当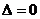 时,
时,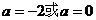 ,
,
若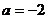 ,则
,则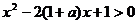 变为
变为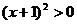 得
得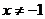 ,
,
此时所求解集为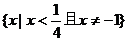 ;
;
若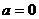 ,则
,则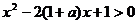 变为
变为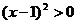 得
得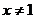 ,
,
此时所求解集为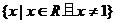 ;
;
③当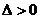 即
即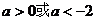 时,
时,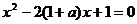 的两根为:
的两根为:
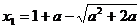 ,
,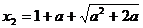
若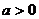 ,则
,则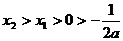 ,
,
此时所求解集为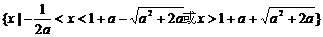
若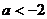 ,则
,则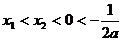 ,
,
此时所求解集为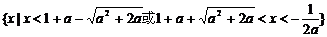
[点睛]本题表面上涉及对数函数,但还是应转化为分式不等式进行处理。对于含参数的不等式,要充分利用不等式的性质,对参数进行讨论,做到不重不漏。
[文]如果{x|2ax2+(2-ab)x-b>0}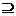 { x|x<-2或x>3},其中b>0,求a、b的取值范围。
{ x|x<-2或x>3},其中b>0,求a、b的取值范围。
解:记A={x|2ax2+(2-ab)x-b>0}={x|(ax+1)(2x-b)>0}
记B={ x|x<-2或x>3}
①若a=0,则A={x>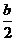 },不可能有A
},不可能有A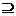 B。
B。
②当a<0时,由(ax+1)(2x-b)=2a(x+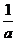 )(x-
)(x-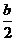 )>0
)>0
知(x+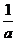 )(x-
)(x-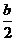 )<0,
)<0,
此不等式的解介于-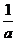 与
与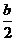 之间的有限区间,故不可能有A
之间的有限区间,故不可能有A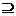 B。
B。
③当a>0时,A={x|x<-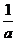 或x>
或x>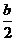 }。∵A
}。∵A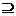 B
B
∴-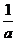 ≥-2且
≥-2且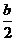 ≤3,∴
≤3,∴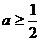 或0<b≤6
或0<b≤6
[点睛]尽管①与②的情形都不可能使A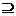 B,但在解题过程中必须讨论.
B,但在解题过程中必须讨论.
[范例4]设a为实数,设函数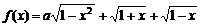 的最大值为g(a)。
的最大值为g(a)。
(Ⅰ)设t=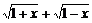 ,求t的取值范围,并把f(x)表示为t的函数m(t)
,求t的取值范围,并把f(x)表示为t的函数m(t)
(Ⅱ)求g(a)
解析:(Ⅰ)令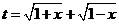 , 要使有t意义,必须1+x≥0且1-x≥0,即-1≤x≤1,
, 要使有t意义,必须1+x≥0且1-x≥0,即-1≤x≤1,
∴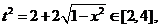 t≥0
①
t≥0
①
t的取值范围是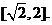 由①得
由①得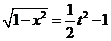
∴m(t)=a(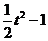 )+t=
)+t=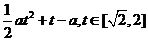
(Ⅱ)由题意知g(a)即为函数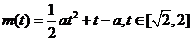 的最大值。
的最大值。
注意到直线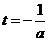 是抛物线
是抛物线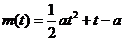 的对称轴,分以下几种情况讨论。
的对称轴,分以下几种情况讨论。
(1)当a>0时,函数y=m(t), 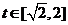 的图象是开口向上的抛物线的一段,
的图象是开口向上的抛物线的一段,
由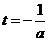 <0知m(t)在
<0知m(t)在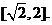 上单调递增,∴g(a)=m(2)=a+2
上单调递增,∴g(a)=m(2)=a+2
(2)当a=0时,m(t)=t, 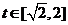 ,∴g(a)=2.
,∴g(a)=2.
(3)当a<0时,函数y=m(t), 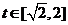 的图象是开口向下的抛物线的一段,
的图象是开口向下的抛物线的一段,
若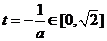 ,即
,即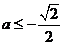 则
则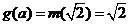
若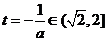 ,即
,即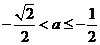 则
则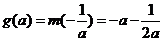
若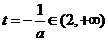 ,即
,即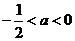 则
则
综上有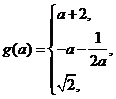
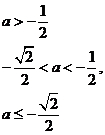
[点睛]本题以函数为背景,考查分类讨论的数学思想方法,体现不等式的工具性.
[文]已知函数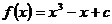 ,定义在
,定义在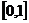 上,
上,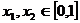 且
且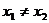
证明:①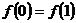 ②
②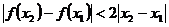 ③
③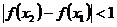
证明:① 略
② 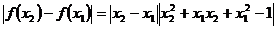 .
.
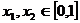 且
且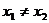
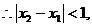
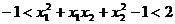 ,
,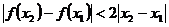 .
.
③不妨设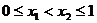 由②可得
由②可得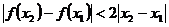 ---------(1)
---------(1)
又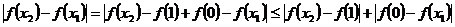
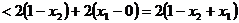 ---------(2)
---------(2)
(1)+(2)得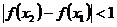
[点睛]采用加减某个式子后,重新组合,运用绝对值不等式的性质变形,是证明绝对值不等式的典型方法.
★★★自我提升
21.舞台说明在戏剧作品中不可或缺,如《雷雨》第二幕开头的舞台说明--“午饭后,天气更阴沉,更郁热。低沉潮湿的空气,使人异常烦躁……”,既交代了故事发生的时间,渲染了气氛,预示着一场雷雨的到来;也可以为塑造人物服务,感染读者或观众。
四川灾区某同学想写一幕短剧,祭奠5·12地震中遇难的老师和同学。请为他写一则舞台说明,表现地震来袭前校园中不为人知的危险气氛。(至少使用两种修辞手法,4分)
答:
。
20.欣赏下面的漫画《参观实验田》,用简明的语言(30字以内)概括其寓意。(4分)

答:
19.请仿照下面一则幽默的形式,另选话题再写两则。(参考话题:悲观、勇敢、怯懦、苦笑、遗憾等)(6分)
例:所谓乐观,打个比方,就像炉灶上的响壶。屁股烧得红红的,却有心情吹口哨。
仿句:①
②
18.为下面则新闻报道拟一个能概括其主要内容的标题。(不超过12个字)(4分)
本报北京2月4日电,据北京市野生动植物保护处负责人介绍,今年北京计划把密云水库湿地、平谷金海湖湿地、顺义汉石桥湿地、门头沟三家店湿地这4处建成市级自然保护区,把全市90%以上的主要湿地建成自然保护区。到2005年,北京的湿地自然保护区将达到10个;到2010年,北京的湿地将恢复到上世纪80年代初期8万公顷的面积。除了增加上游水源供应、退农耕变滩涂外,还将在湿地恢复1万多亩的芦苇植被,恢复植物和动物的多样性。此外,北京今年将尽可能抢救恢复一批重要湿地。
答:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com