
1. 求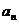 ,若 (1)
,若 (1) 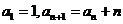 ;(2)
;(2) 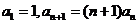 ;(3)
;(3) 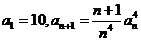
5. 递推数列的常见类型及其解法: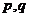 为常数:
为常数:
(0) 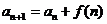 :叠加法,
:叠加法,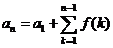 ;
;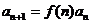 :叠乘法,
:叠乘法,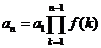
(1) 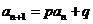 :(1) 不动点法(待定系数法),考虑数列
:(1) 不动点法(待定系数法),考虑数列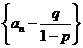 ;(2) 消常法
;(2) 消常法
(2) 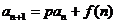 :(1) 两边同除
:(1) 两边同除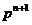 后使用叠加法 .考虑数列
后使用叠加法 .考虑数列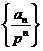 ;(2) 待定系数法
;(2) 待定系数法
(3) 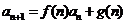 :令
:令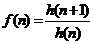 反解出
反解出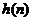 .两边同除
.两边同除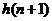 ,考虑数列
,考虑数列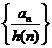 用叠加法.
用叠加法.
(4) 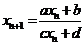 :
: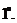 若仅有一个不动点
若仅有一个不动点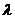 ,则考虑
,则考虑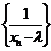
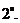 若有两个不动点
若有两个不动点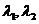 ,则考虑
,则考虑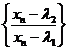
4. 用特征根法解二阶线性递推数列:
设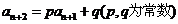 ,则
,则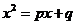 称为其特征方程,特征方程的解叫特征根. 若特征方程:
称为其特征方程,特征方程的解叫特征根. 若特征方程:
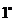 . 有两个不等的根(可以为虚根):
. 有两个不等的根(可以为虚根):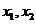 ,则有
,则有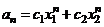 ,其中
,其中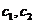 为待定常数,由
为待定常数,由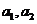 确定
确定
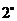 . 有两个相等的(实)根:
. 有两个相等的(实)根: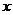 ,则有
,则有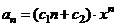 ,其中
,其中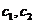 为待定常数,由
为待定常数,由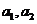 确定 .
确定 .
注:该方法可以推广到任意阶的线性递推数列,若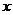 为特征方程的k重根,
为特征方程的k重根,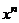 的系数为n的
的系数为n的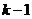 次多项式.
次多项式.
3. 递推数列通项公式的常用求法:
(1) 不动点法;(2) 特征根法;(3) 待定系数法;(4) 数学归纳法;(5) 消常法;(6) 韦达定理
2. 求数列通项公式的基本方法:(1) 转化为等差(比)数列;(2) 赋值相消;(3) 叠加,叠乘法;(4) 换元法
1. k阶递推数列是指由:k个初始值,和递推关系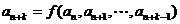 确定的递推数列.(即k推1)
确定的递推数列.(即k推1)
(二)选考题:共10分,请考生从给出的4道题中任选一题做答,并注意所做题目必须与答题纸上对应区域相一致,如果多做,则按所做的第一题计分。
22. (本小题满分10分)(选修4-1:几何证明选讲)
(本小题满分10分)(选修4-1:几何证明选讲)
如图,在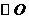 中,
中,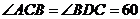 °,
°,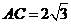 cm
cm
(1)求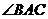 的度数;
的度数;
(2)求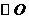 的周长。
的周长。
23. (本小题满分10分)(选修4-2:矩阵与变换)
将曲线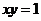 绕坐标原点按逆时针方向旋转45°,求所得曲线的方程。
绕坐标原点按逆时针方向旋转45°,求所得曲线的方程。
24. (本小题满分10分)(选修4-4:坐标系与参数方程)
已知点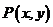 是曲线
是曲线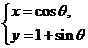 上的一个动点。
上的一个动点。
(1)化曲线的参数方程为普通方程;
(2)求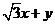 的取值范围。
的取值范围。
25. (本小题满分10分)(选修4-5:不等式选讲)
解不等式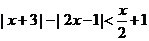




(一)必考题(9题,共80分)
填空题:共4小题,每小题5分
13. 已知双曲线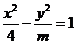 的离心率为2,则实数
的离心率为2,则实数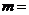 。
。
14. 函数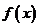 对任意实数
对任意实数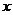 满足条件
满足条件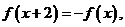 若
若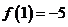 ,则
,则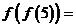
。
15. 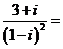 (用
(用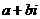 的形式表示,
的形式表示,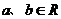 )。
)。
16. 若规定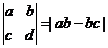 ,则不等式
,则不等式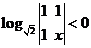 的解集为
。
的解集为
。
解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)
17. (本小题满分12分)
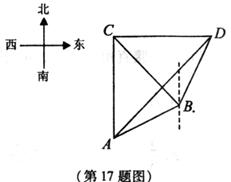 一海轮在
一海轮在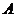 处观察到灯塔
处观察到灯塔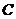 在它的正北方向上,灯塔
在它的正北方向上,灯塔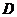 在它的北偏东45°方向上,此海轮从
在它的北偏东45°方向上,此海轮从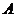 处沿北偏东60°的方向航行了
处沿北偏东60°的方向航行了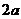 海里到达
海里到达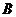 处,在
处,在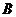 处观测到灯塔
处观测到灯塔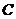 在它的北偏西45°方向上,灯塔
在它的北偏西45°方向上,灯塔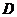 在它的北偏东30°方向上,求
在它的北偏东30°方向上,求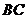 的距离与两灯塔
的距离与两灯塔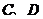 间的距离。
间的距离。
18. (本小题满分12分)
在数列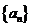 中,
中,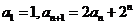 ,
,
(1)设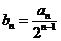 ,证明:数列
,证明:数列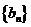 是等差数列;
是等差数列;
(2)求数列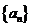 的前
的前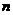 项和
项和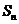 。
。
19. (本小题满分12分)
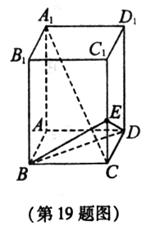 如图所示,在长方体
如图所示,在长方体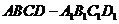 中,
中,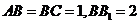 ,连接
,连接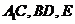 是棱
是棱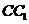 上一点,且
上一点,且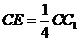 。
。
(1)求三棱锥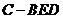 的体积;
的体积;
(2)求证: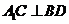
20. (本小题满分12分)
已知圆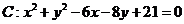 ,直线
,直线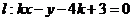 。
。
(1)证明:不论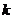 取值何值,直线和圆总有两个不同的焦交点;
取值何值,直线和圆总有两个不同的焦交点;
(2)求当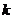 取何值时,直线被圆截得的弦最短,并求出最短弦长。
取何值时,直线被圆截得的弦最短,并求出最短弦长。
21. (本小题满分12分)
 已知
已知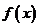 是定义在
是定义在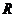 上的奇函数,当
上的奇函数,当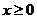 时,
时,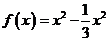 。
。
(1)求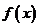 的解析式;
的解析式;
(2)讨论函数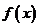 在区间
在区间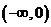 上的单调性;
上的单调性;
(3)设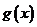 是函数
是函数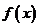 在区间
在区间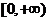 上的导函数,问:是否存在实数
上的导函数,问:是否存在实数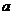 ,满足
,满足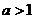 ,并且使
,并且使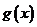 在区间
在区间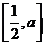 上的值域为
上的值域为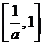 ?若存在,求出
?若存在,求出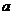 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
12. 表面积为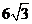 的正四面体各个顶点都在同一球面上,则此球的体积为
的正四面体各个顶点都在同一球面上,则此球的体积为
A、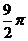 B、
B、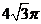 C、36
C、36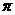 D、
D、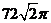
第II卷(非选择题,共90分)
11. 在等腰直角三角形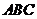 中,在斜边
中,在斜边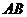 上任取一点
上任取一点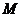 ,则
,则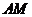 的长小于
的长小于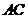 长的概率为
长的概率为
A、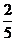 B、
B、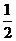 C、
C、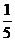 D、
D、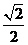
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com