（2）………………………………………………（9分）

 （2）记，若对于一切正整数n，总有T_n≤m成立，求实数m的取值

范围.

（1）f(1)=3………………………………………………………………………………（1分）

        f(2)=6………………………………………………………………………………（2分）

        当x=1时，y=2n，可取格点2n个；当x=2时,y=n，可取格点n个

        ∴f(n)=3n…………………………………………………………………………（4分）

47. 设不等式组所表示的平面区域为D_n，记D_n内的格点（格点即横坐标和纵坐标均为整数的点）的个数为f(n)(n∈N*).

   （1）求f(1)、f(2)的值及f(n)的表达式；（可以不作证明）

当且仅当时取“＝”。                                     …13分

综上可知：若正整数n, m, k成等差数列，不等式 ＋≥总成立。

≥≥。

≤。所以

又因为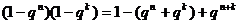

所以≥。                 …10分

若，则，，。    …8分