
7、 要加强 一元二次方程与二次函数之间的综合的训练。
6、 要熟练掌握一元二次方程的几种解法,如因式分解法、公式法等,弄清化一元二次方程为一元一次方程的转化思想。
5、 要弄清一元二次方程的解的概念。
4、 要弄清一元二次方程的定义,ax +bx+c=0(a 0),a,b,c均为常数,尤其a不为零要切记。
3、 要弄清一元一次方程与一次函数、一元一次不等式之间的关系。
2、 要熟练掌握一元一次方程,二元一次方程的解法。
1、 要弄清一元一次方程及二元一次方程组的定义,方程(组)的解(整数解)等概念。
8.在综合实践活动课上,小红准备用两种不同颜色的布料缝制一个正方形座垫,座垫的图案如右图所示,应该选下图中的哪一块布料才能使其与右图拼接符合原来的图案模式. ( )

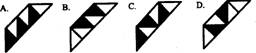
答案:C
例2.如图,“回”字形的道路宽为1米,整个“回”字形的长为8米,宽为7米,…个人从入口点A沿着道路中央走到终点B,他共走了( ).
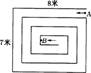 (A)5 5米 (B)5 5.5米 (C)5 6米 (D)5 6.5米
(A)5 5米 (B)5 5.5米 (C)5 6米 (D)5 6.5米
答案:C
例3下面4张扑克牌中,属于中心对称的是 ( )
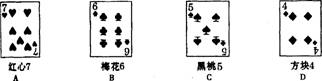
答案:D
例4.一幅美丽的图案,在某个顶点处由四个边长相等的正多边形镶嵌而成,其中的三个分别为正三边形、正四边形、正六边形.那么另外一个为( )
A.正三边形 B.正四边形 C.正五边形 D.正六边形
答案:B
例5.将一个底面半径为2cm高为4cm的圆柱形纸筒沿一条母线剪开,所得到的侧面展开图的面积为__________________cm2;
答案:16a
例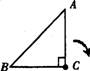 6.如图,在△ABC中,∠C=90°,AC=2cm,把这个三角形在平面内绕点C顺时针旋转90°,那么点A移动所走过的路线长是 cm.(不取近似值)
6.如图,在△ABC中,∠C=90°,AC=2cm,把这个三角形在平面内绕点C顺时针旋转90°,那么点A移动所走过的路线长是 cm.(不取近似值)
答案:π
例7.将如图所示图案绕点O按顺时针方向旋转900,得到的图案是………………( )

例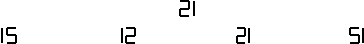 8.小明的运动衣号在镜子中的像是 ,则小明的运动衣号码是……………(
)
8.小明的运动衣号在镜子中的像是 ,则小明的运动衣号码是……………(
)
A. B. C. D.
例9.△ABC平移到△DEF的位置,(即点A与点D,点B与点E,点C与点F,是对应点)有下列说法:①AB=DE;②AD=BE;③BE=CF;④BC=EF其中说法正确个数有……( )
A.1个 B.2个 C.3个 D.4个
例10.下列现象中,不属于旋转变换的是………………………………………………( )
A. 钟摆的运动 B.大风车传动
C. 方向盘的转动 D. 电梯的升降运动
3、会运用三角函数解决与直角三角形有关的简单实际问题。
将继续考查锐角三角形函数的概念,其中特殊三角函数值为考查的重点。解直角三角形为命题的热点,特别是与实际问题结合的应用题
应试对策
1要掌握锐角三角函数的概念,会根据已知条件求一个角的三角函数,会熟练地运用特殊角的三角函数值,会使用科学计算器进行三角函数的求值;
2掌握根据已知条件解直角三角形的方法,运用解直角三角形的知识解决实际问题。具体做到:1)了解某些实际问题中的仰角、俯角、坡度等概念;2)将实际问题转化为数学问题,建立数学模型;3)涉及解斜三角形的问题时,会通过作适当的辅助线构造直角三角形,使之转化为解直角三角形的计算问题而达到解决实际问题
例题精讲
例1、在Rt△ABC中,∠C=90°,a = 1 , c = 4 , 则sinA的值是 ( )
A、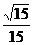 B、
B、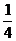 C、
C、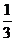 D、
D、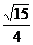
答案:B
例2.在A ABC中,已知∠C=90°,sinB=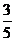 ,则cosA的值是 ( )
,则cosA的值是 ( )
A.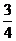 B.
B.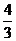 c.
c.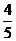 D.
D.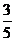
答案:D
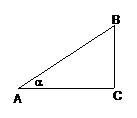 例3.在RtΔABC中,∠C=900,则下列等式中不正确的是( )
例3.在RtΔABC中,∠C=900,则下列等式中不正确的是( )
(A)a=csinA;(B)a=bcotB;(C)b=csinB;
(D)c=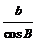 .
.
答案:D
例4.为测楼房BC的高,在距楼房30米的A处,测得楼顶B的仰角为α,则楼房BC的高为( )B
(A) 米;(B)
米;(B)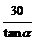 米; (C)
米; (C)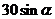 米; (D)
米; (D)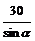 米
米
答案:B
例5.在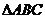 中,
中,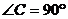 ,
,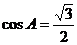 ,则
,则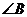 为( )C
为( )C
A.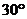 B.
B.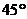 C.
C.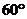 D.
D.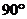
答案:C
例6.如图,是一束平行的阳光从教室窗户射入的平面示意图,光线与地面所成角∠AMC=30°,在教室地面的影长MN=2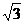 米.若窗户的下檐到教室地面的距离BC=1米,则窗户的上檐到教室的距离AC为( )
米.若窗户的下檐到教室地面的距离BC=1米,则窗户的上檐到教室的距离AC为( )
A.2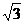 米 B.3米 c.3.2米 D.
米 B.3米 c.3.2米 D.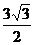 米
米
答案:B
例7.某人沿倾斜角为β的斜坡走了100米,则他上升的高度是 米
答案:100sinβ
例8.如图7,初三年级某班同学要测量校园内国旗旗杆的高度,在地面的C点用测角器测得旗杆顶A点的仰角∠AFE=60°,再沿直线CB后退8米到D点,在D点又用测角器测得旗杆顶A点的仰角∠AGE=45°;已知测角器的高度是1.6米,求旗杆AB的高度.(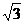 的近似值取1.7,结果保留小数)
的近似值取1.7,结果保留小数)
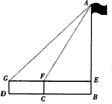
解:设AE为x米,在Rt△EF中,∠AFE=60°,
∴EF=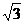 x/3
x/3
在Rt△AGE中,∠AGE=45° AE=GE
8+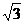 x/3=x ∴x=12+4
x/3=x ∴x=12+4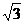
即x≈18.8(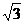 的近似值取1.7,结果保留小数)
的近似值取1.7,结果保留小数)
∴AB=AE+EB≈20.4
答:旗杆高度约为20.4米
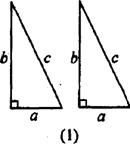
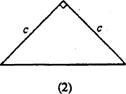
例9.如图(1)是用硬纸板做成的两个全等的直角三角形,两直角边的长分别为a和b,斜边长为c.图(2)是以c为直角边的等腰直角三角形.请你开动脑筋,将它们拼成一个能证明勾股定理的图形。
(1)画出拼成的这个图形的示意图,写出它是什么图形.
(2)用这个图形证明勾股定理.
(3)假设图(1)中的直角三角形有若干个,你能运用图(1)中所给的直角三角形拼出另一种能证明勾股定理的图形吗?请画出拼后的示意图(无需证明)
解:(1)图形规范、正确 写出是直角梯形
(2)S梯形=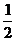 (a-b)2
(a-b)2
S梯形==ab-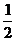 c2
c2
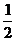 (a-b)2=ab-
(a-b)2=ab-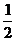 c2 整理,得a2+b2=c2
c2 整理,得a2+b2=c2
(3)拼出能证明勾股定理的图形.
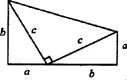
例10.下图表示一山坡路的横截面,CM是一段平路,它高出水平地面24米.从A到B、从B到C是两段不同坡角的山坡路,山坡路AB的路面长100米,它的坡角∠BAE=5°,山坡路BC的坡角∠CBH=12°.为了方便交通,政府决定把山坡路BC的坡角降到与AB的坡角相同,使得∠DBI=5°.(精确到0.O1米)
(1)求山坡路AB的高度BE.
(2)降低坡度后,整个山坡的路面加长了多少米?
(sin5°=0.0872,cos5°=0.9962,sin12°=0.2079,cos12°=0.9781) .

解:(1)在Rt△ABE中,BE=8.72(米)
(2)在Rt△CBH中,CH=CF-HF=15.28.BC=73.497
在Rt△DBI中,DB=175.229
∴DB-BC≈175.229-73.497=101.732≈101.73(米)
2、会由已知锐角求它的三角函数,由已知三角函数值求它对应、的锐角 ;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com