
11.设实数a,b,x,y满足a2+b2=1,x2+y2=3, 则ax+by的取值范围为_______________.
错解: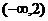
错因: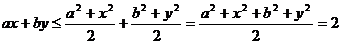 ,当且仅当
,当且仅当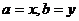 时等号成立,而此时
时等号成立,而此时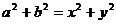 与已知条件矛盾。
与已知条件矛盾。
正解:[-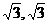 ]
]
10.设x>1,则y=x+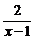 的最小值为___________
的最小值为___________
答案: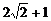
点评:误填:4,错因: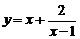 ≥
≥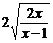 ,当且仅当
,当且仅当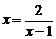 即x=2时等号成立,忽略了运用基本不等式求最值时的“一正、二定、三相等”的条件。
即x=2时等号成立,忽略了运用基本不等式求最值时的“一正、二定、三相等”的条件。
9.不等式|x+1|(2x-1)≥0的解集为____________
答案: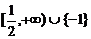
点评:误填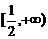 而忽略x=-1。
而忽略x=-1。
8.若α,β,γ为奇函数f(x)的自变量,又f(x)是在(-∞,0)上的减函数,且有α+β>0,α+γ>0,β+γ>0,则f(α)+f(β)与f(-γ)的大小关系是:f(α)+f(β) ______________f(-γ)。正确答案:<
7.不等式 的解集为(-∞,0),则实数a的取值范围是_____________________。
的解集为(-∞,0),则实数a的取值范围是_____________________。
正确答案:{-1,1}
6.不等式(x-2)≥0的解集是 .
正确答案: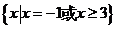
5.不等式ax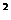 + bx + c>0 ,解集区间(-
+ bx + c>0 ,解集区间(- 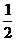 ,2),对于系数a、b、c,则有如下结论:
,2),对于系数a、b、c,则有如下结论:
① a >0 ②b>0 ③ c>0 ④a + b + c>0 ⑤a – b + c>0,其中正确的结论的序号是________________________________.
正确答案 2 、3、 4
错因:一元二次函数的理解
4.若对于任意x∈R,都有(m-2)x2-2(m-2)x-4<0恒成立,则实数m的取值范围是 。
正确答案:(-2,2) 。
错误原因:容易忽视m=2。
3.已知两正数x,y 满足x+y=1,则z=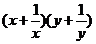 的最小值为
。
的最小值为
。
错解一、因为对a>0,恒有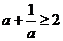 ,从而z=
,从而z=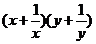
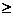 4,所以z的最小值是4。
4,所以z的最小值是4。
错解二、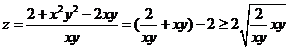
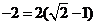 ,所以z的最小值是
,所以z的最小值是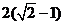 。
。
错解分析:解一等号成立的条件是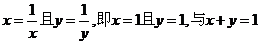 相矛盾。解二等号成立的条件是
相矛盾。解二等号成立的条件是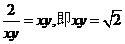 ,与
,与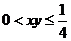 相矛盾。
相矛盾。
正解:z=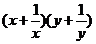 =
=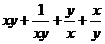 =
=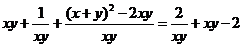 ,令t=xy, 则
,令t=xy, 则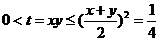 ,由
,由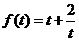 在
在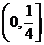 上单调递减,故当t=
上单调递减,故当t=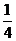 时
时 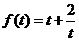 有最小值
有最小值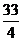 ,所以当
,所以当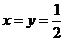 时z有最小值
时z有最小值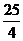 。
。
2.若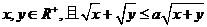 恒成立,则a的最小值是
恒成立,则a的最小值是
错解:不能灵活运用平均数的关系,正解:由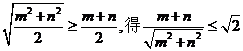 ,即
,即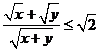 ,故a的最小值是
,故a的最小值是 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com