
22.已知圆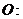
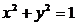 ,点O为坐标原点,一条直线
,点O为坐标原点,一条直线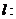
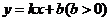 与圆O相切并与椭圆
与圆O相切并与椭圆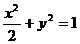 交于不同的两点A、B。
交于不同的两点A、B。
(Ⅰ)设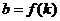 ,求
,求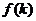 的表达式,并注明
的表达式,并注明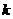 的取值范围;( 3分 )
的取值范围;( 3分 )
(Ⅱ)若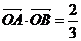 ,求直线
,求直线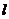 的方程;( 5分 )
的方程;( 5分 )
(Ⅲ)若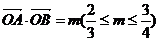 ,求
,求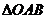 面积
面积 的取值范围。( 6分 )
的取值范围。( 6分 )
福建省永春一中、培元中学、季延中学、石光华侨联中2010届高三上学期期末联考
21.已知函数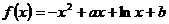 .
.
(Ⅰ)若函数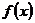 在
在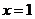 处的切线方程为
处的切线方程为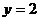 ,求
,求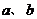 的值;( 4分 )
的值;( 4分 )
(Ⅱ)若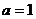 ,函数
,函数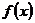 的图象能否总在直线
的图象能否总在直线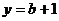 的下方?若能,请加以证明;若不能,请说明理由。( 8分 )
的下方?若能,请加以证明;若不能,请说明理由。( 8分 )
20.数列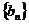
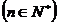 是递增的等比数列,且
是递增的等比数列,且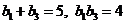 。
。
(Ⅰ)求数列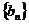 的通项公式;( 4分 )
的通项公式;( 4分 )
(Ⅱ)若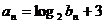 , 求证数列
, 求证数列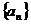 是等差数列;( 4分 )
是等差数列;( 4分 )
(Ⅲ)若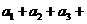 …
…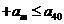 , 求
, 求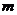 的最大值。 ( 4分 )
的最大值。 ( 4分 )
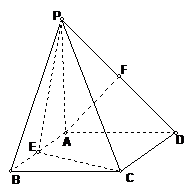
19.如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,
PA=2,∠PDA=45°,点E、F分别为棱AB、PD的中点。
(Ⅰ)求证:AF∥平面PCE;( 4分 )
(Ⅱ)求证:平面PCE⊥平面PCD;( 4分 )
(Ⅲ)求三棱锥C-BEP的体积。( 4分 )
18.设函数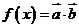 ,其中向量
,其中向量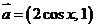 ,
,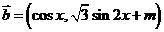
(Ⅰ)当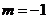 时,求函数
时,求函数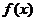 的最小值,并求此时
的最小值,并求此时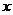 的值;( 6分 )
的值;( 6分 )
 (Ⅱ)当
(Ⅱ)当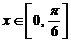 时,
时,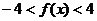 恒成立,求实数
恒成立,求实数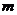 的取值范围。( 6分 )
的取值范围。( 6分 )
17.袋子中有质地、大小完全相同的4个球,编号分别为1,2,3,4.甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,若两个编号的和为奇数算甲赢,否则算乙赢.记基本事件为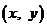 ,其中
,其中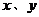 分别为甲、乙摸到的球的编号
分别为甲、乙摸到的球的编号
(Ⅰ)列举出所有的基本事件,并求甲赢且编号的和为5的事件发生的概率;( 6分 )
(Ⅱ)比较甲胜的概率与乙胜的概率,并说明这种游戏规则是否公平。( 6分 )
16.已知数列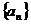 的通项公式
的通项公式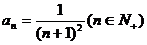 ,记
,记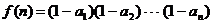 ,试通过计算
,试通过计算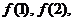
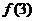 的值,推测出
的值,推测出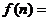 。
。
15.如图,矩形长为6,宽为4,在矩形内随机地撒300颗黄豆,
数得落在椭圆外的黄豆数为96颗,以此实验数据为依据可以
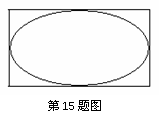 估计出椭圆的面积约为
。
估计出椭圆的面积约为
。
14.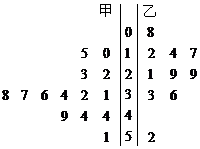 如右图是甲、乙两名篮球运动员某赛季一些场次得分的茎叶图,
如右图是甲、乙两名篮球运动员某赛季一些场次得分的茎叶图,
茎表示得分的十位数,据图可知甲运动员得分的中位数和乙运动员
得分的众数分别为 、 。
请把答案填在答题卡的横线上。
13.如图所示,这是计算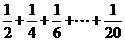 的值的一个程
的值的一个程
序框图,其中判断框内应填入的条件是 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com