
例4 已知函数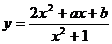 的值域为[1,3],求a、b的值。
的值域为[1,3],求a、b的值。
解:由题意知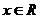 ,把原函数变形为
,把原函数变形为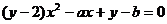
当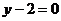 时,满足题意
时,满足题意
当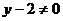 时,因
时,因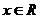 ,所以
,所以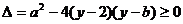 ,即
,即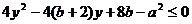 。因
。因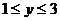 ,所以1和3是方程
,所以1和3是方程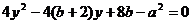 的两个实根,由韦达定理解得
的两个实根,由韦达定理解得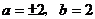 。
。
注:解决此问题的关键在于把求值域的问题和解一元二次不等式的问题联系起来,最后通过比较同解不等式的系数,列方程求出参数的值。
例3 已知函数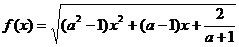 的定义域为R,求实数a的取值范围。
的定义域为R,求实数a的取值范围。
解:由题意知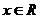 时,
时,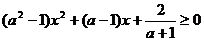 恒成立。
恒成立。
(1)当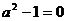 且
且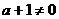 时,有a=1,此时f(x)=1,显然对
时,有a=1,此时f(x)=1,显然对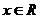 时,
时,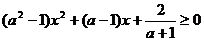 恒成立。
恒成立。
(2)当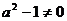 时,有
时,有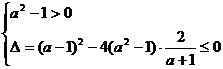 解不等式组得
解不等式组得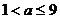 。
。
综上知,当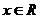 时,使得
时,使得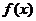 有意义的a的取值范围是[1,9]。
有意义的a的取值范围是[1,9]。
注:此问题转化为不等式恒成立问题,但要注意二次函数的二次项系数为字母时的分类讨论。
例2 已知函数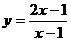 的值域是
的值域是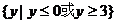 ,求此函数的定义域。
,求此函数的定义域。
解:由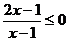 ,解得
,解得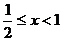 。
。
由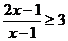 ,解得
,解得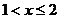 。
。
∴此函数的定义域为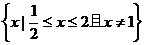 。
。
注:此题直接由函数值域得出表达式的不等式,进而求得定义域,同时还可以利用反比例函数图象直观地得出结论,同学们不妨试一试。
例1 求定义域在[-1,1]上的函数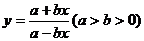 的值域。
的值域。
解:函数式变形为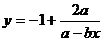 ,显然y≠-1
,显然y≠-1
由原函数表达式可得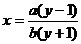 。
。
又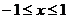 ,得
,得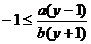
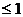 ,
,
解得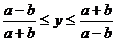 ,
,
即此函数的值域为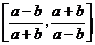 。
。
注:此法是把函数式视为关于x的方程,解出x,再运用已知的定义域,解关于y的不等式求得值域。
例4:设定义在[-2,2]上的偶函数在区间[0,2]上单调递减,若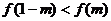 ,求实数m的取值范围。
,求实数m的取值范围。
分析:由函数的定义域知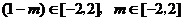 ,但是
,但是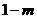 与m到底是在[-2,0]、[0,2]的哪个区域内,不十分清楚,若就此讨论,将十分复杂,如果注意到性质“如果是偶函数,那么
与m到底是在[-2,0]、[0,2]的哪个区域内,不十分清楚,若就此讨论,将十分复杂,如果注意到性质“如果是偶函数,那么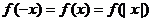 ”,问题解答就简捷多了。
”,问题解答就简捷多了。
解: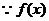 是偶函数,
是偶函数,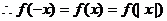 ,
,
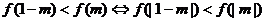
又当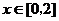 时,
时,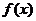 单调递减,
单调递减,
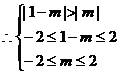 ,解得
,解得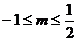
点评:本题应用了偶函数的一个简单性质,从而避免了一场“大规模”的讨论,将“曲径”变“通途”。值得深思。
|
年级 |
高中 |
学科 |
数学 |
版本 |
|
期数 |
|
||||||
|
内容标题 |
如何避免“分类讨论” |
||||||||||||
|
分类索引号 |
G.622.46 |
分类索引描述 |
辅导与自学 |
||||||||||
|
主题词 |
如何避免“分类讨论” |
栏目名称 |
专题辅导 |
||||||||||
|
供稿老师 |
|
审稿老师 |
|
||||||||||
|
录入 |
张玲 |
一校 |
陈丽娜 |
二校 |
|
审核 |
|
||||||
例3:设不等式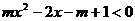 对于满足
对于满足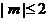 的一切m的值都成立,求m的取值范围。
的一切m的值都成立,求m的取值范围。
分析:本例为含参数的不等式,关键是对参数的处理,从表面上看,是一个关于x的一元二次不等式,实质上是一个关于m的一元一次不等式,并且已知它的解集为[-2,2],求参数的范围。因此通过参数m与未知数x的地位的变化,借助于一次函数图象,避免了繁杂的对参数的讨论。
解:设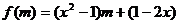 ,它是以m为自变量的一次函数,其图象为直线,由题意知,这条直线当
,它是以m为自变量的一次函数,其图象为直线,由题意知,这条直线当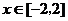 时,线段在y轴的下方,满足它的为
时,线段在y轴的下方,满足它的为
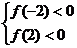 即
即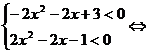
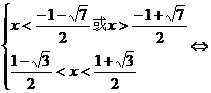
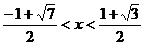
例2:设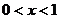 ,
,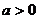 且
且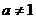 ,比较
,比较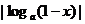 与
与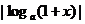 的大小。
的大小。
分析:本例通常应分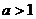 与
与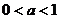 两种情况讨论,但运用换底公式消去a,就可避免分类讨论,从而达到简化解题过程的目的。
两种情况讨论,但运用换底公式消去a,就可避免分类讨论,从而达到简化解题过程的目的。
解:运用作商比较法,
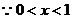 ,
,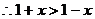 ,
,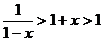
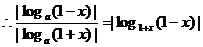
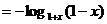
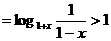
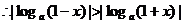
例1:奇函数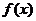 是R上的减函数,若对任意的
是R上的减函数,若对任意的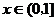 ,不等式
,不等式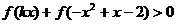 恒成立,求实数k的取值范围。
恒成立,求实数k的取值范围。
解: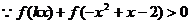 ,且
,且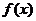 是R上的奇函数,减函数,
是R上的奇函数,减函数,
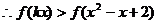
得到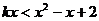 (1)
(1)
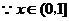 ,可得
,可得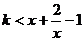 ,问题转化为只要k小于
,问题转化为只要k小于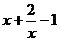 的最小值即可。
的最小值即可。
令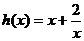 ,因为
,因为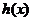 在(0,
在(0,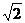 )上是减函数,
)上是减函数,
故当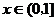 时,
时,
显然有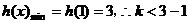 ,即
,即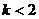
∴k的取值范围为(-∞,2)
点评:按照常规思路,由(1)式转化为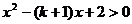 在
在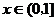 上恒成立问题,可令
上恒成立问题,可令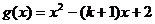 ,然后根据二次函数性质及对称轴位置的变化,进行分类讨论,得到:
,然后根据二次函数性质及对称轴位置的变化,进行分类讨论,得到:
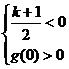 或
或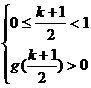 或
或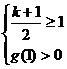
解得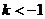 或
或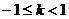 或
或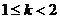 ,从而求得k的取值范围为(-∞,2)。这样解就显得比较烦琐,因为有些不等式在区间上的“恒成立”问题,一般通过分离变量,转化为函数的最值问题求解。就可以避免分类讨论,使得解题过程简明快捷,少走弯路。
,从而求得k的取值范围为(-∞,2)。这样解就显得比较烦琐,因为有些不等式在区间上的“恒成立”问题,一般通过分离变量,转化为函数的最值问题求解。就可以避免分类讨论,使得解题过程简明快捷,少走弯路。
20. 已知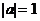 ,
,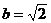
(1)若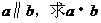 ;
;
(2)若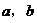 的夹角为135°,求|a+b|。
的夹角为135°,求|a+b|。
19. 已知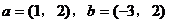 ,当k为何值时,
,当k为何值时,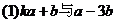 垂直?(2)
垂直?(2)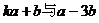 平行?平行时它们是同向还是反向?
平行?平行时它们是同向还是反向?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com