
例3. 5个相同小球放到4个不同盒子里,每盒至少有1个,共有多少种放法?
解法1:每盒先放入1球,剩下1球任选1盒,共有: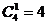 (种)放法。
(种)放法。
解法2:(第一隔板法)
5个小球可形成6个空隙,由于每盒至少放1个小球,所以除去两边空隙还剩4个空,只要在这4个位置上隔进3个板,即可满足要求。所以有: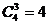 (种)放法。
(种)放法。
例4. 将5个相同小球放到4个不同盒子里(盒子可空),共有多少种放法?
解法1:(分类法)
第一类:全部放入1个盒子里,有: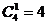 (种)放法;
(种)放法;
第二类:放入2个盒子里,有: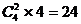 (种)放法;
(种)放法;
第三类:放入3个盒子里,有: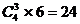 (种)放法;
(种)放法;
第四类:放入4个盒子里,有4种放法。
所以,共有:4+24+24+4=56(种)放法。
解法2:(第二隔板法)
将4个盒子与5个小球看成9个相同元素,除去两边形成8个空隙,将这8个空隙隔进3个板,即有: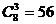 (种)放法。
(种)放法。
一般地,相同元素分组,可用隔板法。如果每组至少一个元素可用第一隔板法,如果没有要求可用第二隔板法。
相关练习:
1. 某校准备参加2006年全国数学联赛,把10个名额分给高三8个班,每班至少1人,不同的分配方案有几种?(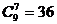 )
)
例2. 小麦、大麦品种各1种,种在5种不同土质的试验田里,3块种小麦,2块种大麦,有多少种种法?
解:这5个不尽相异的元素有3个相同,另2个相同,所以共有: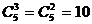 (种)种法。
(种)种法。
一般地,在n个不尽相异的元素里,如果有m1个元素相同,又有m2个元素相同,并且m1+m2=n,那么这n个元素的不同排列种数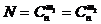 。
。
例1. 4个同学争夺3项竞赛冠军,冠军获得者共有几种可能情况?
解:完成这件事情可分三步:(1)第一项冠军有4种可能;(2)第二项冠军有4种可能;(3)第三项冠军有4种可能。所以可能情况有:4×4×4=64(种)。
一般地,从n个不同元素里取出允许重复的m个元素,按一定顺序排成一列,那么,第1、第2、…、第m个位置上选取元素的方法都有n种。由分步计数原理得每次从n个不同元素里取出允许重复的m个元素的排列数为:
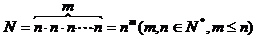
相关练习:
用0,1,2,…,9这10个数字可组成多少个8位数字的电话号码?(108)
2. 引伸,推广成定理
定理:若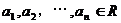 ,则
,则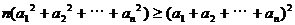
证明:因为n个数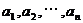 的方差
的方差
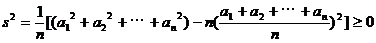 ,
,
化简得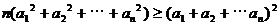 。
。
当且仅当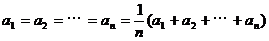 时,取“=”号。
时,取“=”号。
该定理反映了“n个数的平方和”与“n个数的和的平方”之间的内在联系。
例4. 已知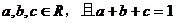 ,求证
,求证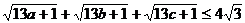
证明:由定理知
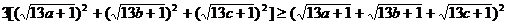
所以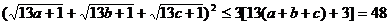 ,
,
即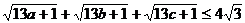 。
。
当且仅当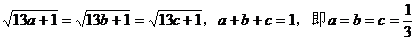 时取“=”号。
时取“=”号。
例2. 已知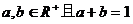 ,求证
,求证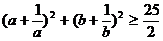
证明:由定理知
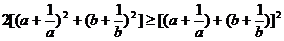 ,
,
所以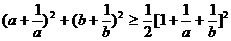
又知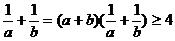 ,
,
所以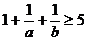 ,
,
则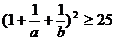
所以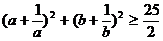
当且仅当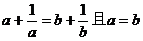 ,即
,即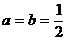 时取“=”号。
时取“=”号。
例3. 设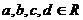 ,且
,且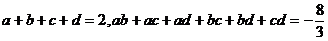 ,求
,求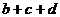 的最大值与最小值。
的最大值与最小值。
解:由以上定理知
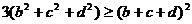 (1)
(1)
令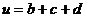
则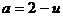 (2)
(2)
又知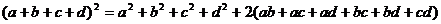 ,
,
所以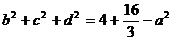 (3)
(3)
(2),(3)代入(1)式得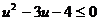 ,
,
所以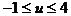
可知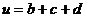 的最大值为4,此时
的最大值为4,此时
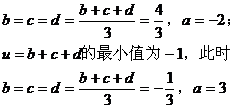
|
年级 |
高中 |
学科 |
数学 |
版本 |
|
期数 |
|
||||||
|
内容标题 |
方差在解题中的应用 |
||||||||||||
|
分类索引号 |
G.622.46 |
分类索引描述 |
辅导与自学 |
||||||||||
|
主题词 |
方差在解题中的应用 |
栏目名称 |
专题辅导 |
||||||||||
|
供稿老师 |
|
审稿老师 |
|
||||||||||
|
录入 |
常丽霞 |
一校 |
胡丹 |
二校 |
|
审核 |
|
||||||
1. 巧用方差解题
例1. 已知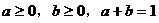 ,求证:
,求证: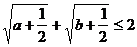
证明:令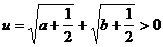 ,则
,则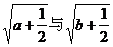 的平均数
的平均数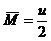 。
。
方差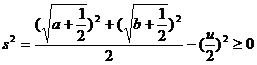
整理得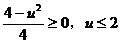 ,
,
即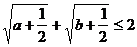
当且仅当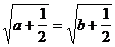 ,且
,且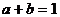 ,即
,即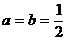 时取“=”号。
时取“=”号。
例2. 已知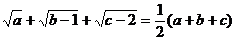 ,求
,求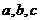 的值。
的值。
分析:数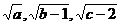 的平均数
的平均数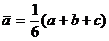
方差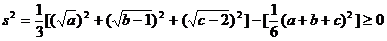
整理得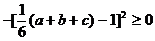
当且仅当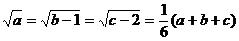 时取“=”号。
时取“=”号。
又知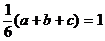
所以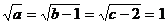
求得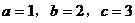
例3. 求满足方程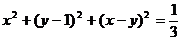 的一切实数x,y的值。
的一切实数x,y的值。
解:设数据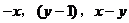 的平均数为
的平均数为
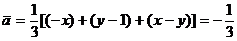
方差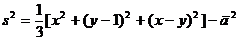
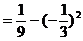
当且仅当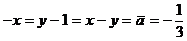 时,
时,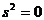
此时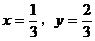
小结:在构造不等式中,要设法使不等号的一边变成常数和注意等号成立的条件。
常用于解决整数分解型排列、组合的问题。
例9. 有10个三好学生名额,分配到6个班,每班至少1个名额,共有多少种不同的分配方案?
解:6个班,可用5个隔板,将10个名额并排成一排,名额之间有9个空,将5个隔板插入9个空,每一种插法,对应一种分配方案,故方案有: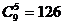 (种)
(种)
|
年级 |
高中 |
学科 |
数学 |
版本 |
|
期数 |
|
||||||
|
内容标题 |
排列组合的常见题型及其解法 |
||||||||||||
|
分类索引号 |
G.622.475 |
分类索引描述 |
统考试题与题解 |
||||||||||
|
主题词 |
排列组合的常见题型及其解法 |
栏目名称 |
专题辅导 |
||||||||||
|
供稿老师 |
|
审稿老师 |
|
||||||||||
|
录入 |
韩秋荣 |
一校 |
胡丹 |
二校 |
|
审核 |
|
||||||
处理排列、组合综合性问题一般是先选元素,后排列。
例8. 将4名教师分派到3所中学任教,每所中学至少1名教师,则不同的分派方案共有多少种?
解:可分两步进行:第一步先将4名教师分为三组(1,1,2),(2,1,1),(1,2,1),共有: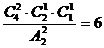 (种),第二步将这三组教师分派到3种中学任教有
(种),第二步将这三组教师分派到3种中学任教有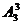 种方法。由分步计数原理得不同的分派方案共有:
种方法。由分步计数原理得不同的分派方案共有: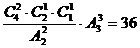 (种)。因此共有36种方案。
(种)。因此共有36种方案。
按题目条件,把符合条件的排列、组合问题分成互不重复的若干类,分别计算,最后计算总数。
例7. 已知直线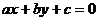 中的a,b,c是取自集合{-3,-2,-1,0,1,2,3}中的3个不同的元素,并且该直线的倾斜角为锐角,求符合这些条件的直线的条数。
中的a,b,c是取自集合{-3,-2,-1,0,1,2,3}中的3个不同的元素,并且该直线的倾斜角为锐角,求符合这些条件的直线的条数。
解:设倾斜角为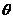 ,由
,由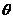 为锐角,得
为锐角,得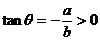 ,即a,b异号。
,即a,b异号。
(1)若c=0,a,b各有3种取法,排除2个重复(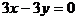 ,
,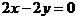 ,
,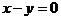 ),故有:3×3-2=7(条)。
),故有:3×3-2=7(条)。
(2)若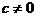 ,a有3种取法,b有3种取法,而同时c还有4种取法,且其中任意两条直线均不相同,故这样的直线有:3×3×4=36(条)。
,a有3种取法,b有3种取法,而同时c还有4种取法,且其中任意两条直线均不相同,故这样的直线有:3×3×4=36(条)。
从而符合要求的直线共有:7+36=43(条)
对于某些比较复杂的或抽象的排列问题,可以采用转化思想,从问题的反面去考虑,先求出无限制条件的方法种数,然后去掉不符合条件的方法种数。在应用此法时要注意做到不重不漏。
例6. 四面体的顶点和各棱中点共有10个点,取其中4个不共面的点,则不同的取法共有( )
A. 150种 B. 147种 C. 144种 D. 141种
解:从10个点中任取4个点有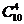 种取法,其中4点共面的情况有三类。第一类,取出的4个点位于四面体的同一个面内,有
种取法,其中4点共面的情况有三类。第一类,取出的4个点位于四面体的同一个面内,有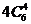 种;第二类,取任一条棱上的3个点及该棱对棱的中点,这4点共面,有6种;第三类,由中位线构成的平行四边形(其两组对边分别平行于四面体相对的两条棱),它的4个点共面,有3种。以上三类情况不合要求应减掉,所以不同的取法共有:
种;第二类,取任一条棱上的3个点及该棱对棱的中点,这4点共面,有6种;第三类,由中位线构成的平行四边形(其两组对边分别平行于四面体相对的两条棱),它的4个点共面,有3种。以上三类情况不合要求应减掉,所以不同的取法共有: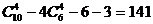 (种)。
(种)。
对于把几个元素分成若干排的排列问题,若没有其他特殊要求,可采取统一成一排的方法求解。
例5. 9个人坐成三排,第一排2人,第二排3人,第三排4人,则不同的坐法共有多少种?
解:9个人可以在三排中随意就坐,无其他限制条件,所以三排可以看作一排来处理,不同的坐标共有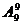 种。
种。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com