
对于在排列中,当某些元素次序一定时,可用此法。解题方法是:先将n个元素进行全排列有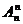 种,
种,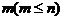 个元素的全排列有
个元素的全排列有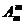 种,由于要求m个元素次序一定,因此只能取其中的某一种排法,可以利用除法起到调序的作用,即若n个元素排成一列,其中m个元素次序一定,则有
种,由于要求m个元素次序一定,因此只能取其中的某一种排法,可以利用除法起到调序的作用,即若n个元素排成一列,其中m个元素次序一定,则有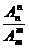 种排列方法。
种排列方法。
例4. 由数字0、1、2、3、4、5组成没有重复数字的六位数,其中个位数字小于十位数字的六位数有多少个?
解:不考虑限制条件,组成的六位数有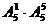 种,其中个位与十位上的数字一定,所以所求的六位数有:
种,其中个位与十位上的数字一定,所以所求的六位数有:
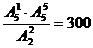 (个)
(个)
元素相离(即不相邻)问题,可以先将其他元素排好,然后再将不相邻的元素插入已排好的元素位置之间和两端的空中。
例3. 7人排成一排,甲、乙、丙3人互不相邻有多少种排法?
解:先将其余4人排成一排,有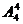 种,再往4人之间及两端的5个空位中让甲、乙、丙插入,有
种,再往4人之间及两端的5个空位中让甲、乙、丙插入,有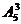 种,所以排法共有:
种,所以排法共有: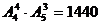 (种)
(种)
对于要求某几个元素必须排在一起的问题,可用“捆绑法”:即将这几个元素看作一个整体,视为一个元素,与其他元素进行排列,然后相邻元素内部再进行排列。
例2. 5个男生和3个女生排成一排,3个女生必须排在一起,有多少种不同排法?
解:把3个女生视为一个元素,与5个男生进行排列,共有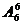 种,然后女生内部再进行排列,有
种,然后女生内部再进行排列,有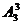 种,所以排法共有:
种,所以排法共有: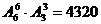 (种)。
(种)。
把有限制条件的元素(位置)称为特殊元素(位置),对于这类问题一般采取特殊元素(位置)优先安排的方法。
例1. 6人站成一横排,其中甲不站左端也不站右端,有多少种不同站法?
分析:解有限制条件的元素(位置)这类问题常采取特殊元素(位置)优先安排的方法。
解法1:(元素分析法)因为甲不能站左右两端,故第一步先让甲排在左右两端之间的任一位置上,有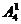 种站法;第二步再让其余的5人站在其他5个位置上,有
种站法;第二步再让其余的5人站在其他5个位置上,有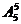 种站法,故站法共有:
种站法,故站法共有: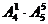 =480(种)
=480(种)
解法2:(位置分析法)因为左右两端不站甲,故第一步先从甲以外的5个人中任选两人站在左右两端,有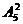 种;第二步再让剩余的4个人(含甲)站在中间4个位置,有
种;第二步再让剩余的4个人(含甲)站在中间4个位置,有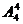 种,故站法共有:
种,故站法共有: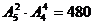 (种)
(种)
证明:设点A(m,n)是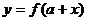 图象上任一点,即
图象上任一点,即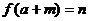 ,点A关于点
,点A关于点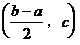 的对称点为
的对称点为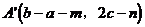
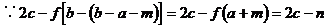
∴点A'在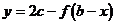 的图象上
的图象上
反过来,同样可以证明,函数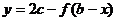 图象上任一点关于点
图象上任一点关于点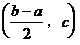 的对称点在函数
的对称点在函数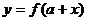 图象上。
图象上。
故函数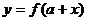 与函数
与函数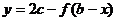 的图象关于点
的图象关于点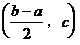 对称。
对称。
说明:此命题同样可以从图象变换的角度去理解。
|
年级 |
高中 |
学科 |
数学 |
版本 |
|
期数 |
|
||||||
|
内容标题 |
抽象函数图象的对称问题 |
||||||||||||
|
分类索引号 |
G.622.46 |
分类索引描述 |
辅导与自学 |
||||||||||
|
主题词 |
抽象函数图象的对称问题 |
栏目名称 |
专题辅导 |
||||||||||
|
供稿老师 |
|
审稿老师 |
|
||||||||||
|
录入 |
李红英 |
一校 |
胡丹 |
二校 |
|
审核 |
|
||||||
证明:设点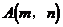 是
是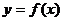 图象上任一点,则
图象上任一点,则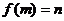 ,点A关于点
,点A关于点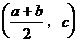 的对称点为
的对称点为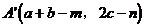 。
。
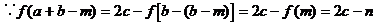
∴点A'也在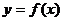 的图象上,故
的图象上,故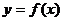 的图象关于点
的图象关于点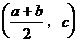 对称
对称
说明:(1)当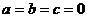 时,奇函数图象关于点(0,0)对称。(2)易知此命题的逆命题也成立。
时,奇函数图象关于点(0,0)对称。(2)易知此命题的逆命题也成立。
证明:设点A(m,n)是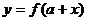 图象上任一点,即
图象上任一点,即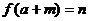 ,点A关于直线
,点A关于直线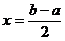 的对称点为
的对称点为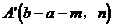 。
。
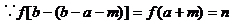
∴点A'在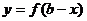 的图象上
的图象上
反过来,同样可以证明,函数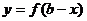 图象上任一点关于直线
图象上任一点关于直线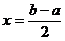 的对称点也在函数
的对称点也在函数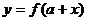 的图象上,故函数
的图象上,故函数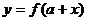 与函数
与函数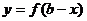 的图象关于直线
的图象关于直线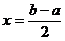 对称。
对称。
说明:可以从图象变换的角度去理解此命题。
易知,函数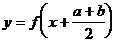 与
与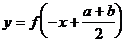 的图象关于直线
的图象关于直线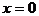 对称,由
对称,由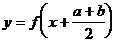 的图象平移得到
的图象平移得到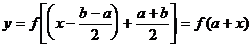 的图象,由
的图象,由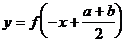 的图象平移得到
的图象平移得到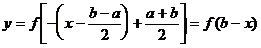 的图象,它们的平移方向和长度是相同的,故函数
的图象,它们的平移方向和长度是相同的,故函数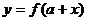 与函数
与函数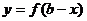 的图象关于直线
的图象关于直线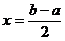 对称。
对称。
证明:设点A(m,n)是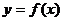 图象上任一点,即
图象上任一点,即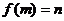 ,点A关于直线
,点A关于直线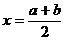 的对称点为
的对称点为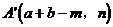 。
。
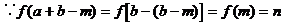
∴点A'也在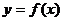 的图象上,故
的图象上,故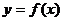 的图象关于直线
的图象关于直线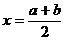 对称。
对称。
例4. 如图3所示,正六边形PABCDE的边长为b,有五个力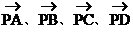 、
、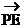 作用于同一点P,求五个力的合力。
作用于同一点P,求五个力的合力。
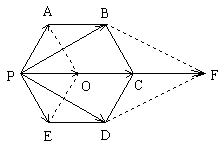
图3
解:所求五个力的合力为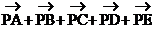 ,如图3所示,以PA、PE为边作平行四边形PAOE,则
,如图3所示,以PA、PE为边作平行四边形PAOE,则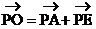 ,由正六边形的性质可知
,由正六边形的性质可知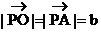 ,且O点在PC上,以PB、PD为边作平行四边形PBFD,则
,且O点在PC上,以PB、PD为边作平行四边形PBFD,则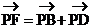 ,由正六边形的性质可知
,由正六边形的性质可知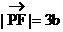 ,且F点在PC的延长线上。
,且F点在PC的延长线上。
由正六边形的性质还可求得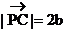
故由向量的加法可知所求五个力的合力的大小为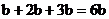 ,方向与
,方向与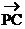 的方向相同。
的方向相同。
|
年级 |
高中 |
学科 |
数学 |
版本 |
|
期数 |
|
||||||
|
内容标题 |
平面向量的应用 |
||||||||||||
|
分类索引号 |
G.622.46 |
分类索引描述 |
辅导与自学 |
||||||||||
|
主题词 |
平面向量的应用 |
栏目名称 |
专题辅导 |
||||||||||
|
供稿老师 |
|
审稿老师 |
|
||||||||||
|
录入 |
许咏梅 |
一校 |
陈丽娜 |
二校 |
|
审核 |
|
||||||
例3. 证明不等式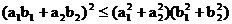
证明:设向量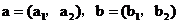 ,则
,则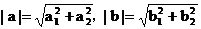 ,设a与b的夹角为θ,
,设a与b的夹角为θ,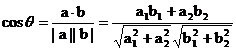
又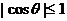
则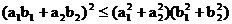
当且仅当a、b共线时取等号。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com