
在解决某些涉及若干个量的求值问题时,要有目标意识,通过虚设的策略,整体转化的思想,绕开复杂的运算过程,可使问题迅速得到解决。
例1. 已知等比数列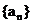 中,
中,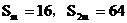 ,求
,求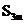 。
。
解:设公比为q,由于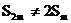 ,故
,故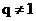
于是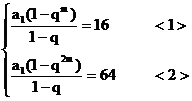
<2>÷<1>得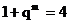 ,则
,则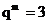
所以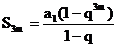
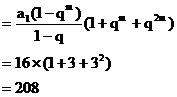
4. 善于转化。在斜三角形中添置适当的辅助线,使其转化为解直角三角形的问题。
例1. 如图1,在△ABC中,C=90°,如果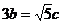 ,则sinA=________。
,则sinA=________。
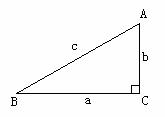
图1
解法1:设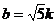 ,则
,则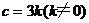 ,根据勾股定理,得
,根据勾股定理,得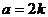 。
。
∴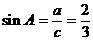
解法2:由已知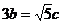 ,得
,得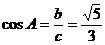
∴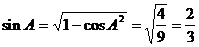
例2. 如图2,在△ABC中,A=30°,∠ACB=105°,AC=15,则BC的长是_________。
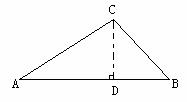
图2
解:过点C作CD⊥AB于点D,
在Rt△ACD中,A=30°,
所以CD=AC·sinA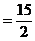
∠DBC=180°-105°-30°=45°
在Rt△BCD中,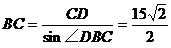 。
。
|
年级 |
高中 |
学科 |
数学 |
版本 |
|
期数 |
|
||||||
|
内容标题 |
解直角三角形知识回顾 |
||||||||||||
|
分类索引号 |
G.622.46 |
分类索引描述 |
辅导与自学 |
||||||||||
|
主题词 |
解直角三角形知识回顾 |
栏目名称 |
专题辅导 |
||||||||||
|
供稿老师 |
|
审稿老师 |
|
||||||||||
|
录入 |
蔡卫琴 |
一校 |
胡丹 |
二校 |
|
审核 |
|
||||||
3. 要注意数与形相结合。充分利用图形,能根据图形特征巧妙寻找解题途径。
2. 熟记30°、45°、60°角的三角函数值。能根据已知锐角求出它的三角函数值,或由三角函数值求出相应的锐角。初步认识锐角三角函数的增减情况。
1. 重视基本概念的形成过程。明确三角函数的值只与角的大小有关,与直角三角形边的长度无关。
例7. 若a,b,c是三角形的三边长,证明长为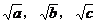 的三条线段能构成锐角三角形。
的三条线段能构成锐角三角形。
错解:不妨设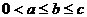 ,只要考虑最大边的对角θ为锐角即可。
,只要考虑最大边的对角θ为锐角即可。
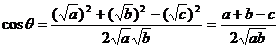 。
。
由于a,b,c是三角形的三边长,根据三角形三边关系,有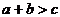 ,即
,即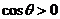 。
。
∴长为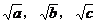 的三条线段能构成锐角三角形。
的三条线段能构成锐角三角形。
辨析:三条线段构成锐角三角形,要满足两个条件:①三条边满足三角形边长关系;②最长线段的对角是锐角。显然错解只验证了第二个条件,而缺少第一个条件。
正解:由错解可得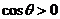
又∵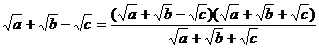
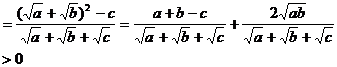
即长为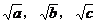 的三条线段能构成锐角三角形。
的三条线段能构成锐角三角形。
|
年级 |
高中 |
学科 |
数学 |
版本 |
|
期数 |
|
||||||
|
内容标题 |
解斜三角形及其应用错解分析 |
||||||||||||
|
分类索引号 |
G.622.46 |
分类索引描述 |
辅导与自学 |
||||||||||
|
主题词 |
解斜三角形及其应用错解分析 |
栏目名称 |
专题辅导 |
||||||||||
|
供稿老师 |
|
审稿老师 |
|
||||||||||
|
录入 |
蔡卫琴 |
一校 |
陈丽娜 |
二校 |
|
审核 |
|
||||||
例6. 在△ABC中,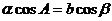 ,判断△ABC的形状。
,判断△ABC的形状。
错解:在△ABC中,∵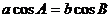 ,由正弦定理
,由正弦定理
得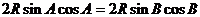
∴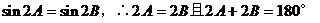
∴A=B且A+B=90°
故△ABC为等腰直角三角形。
辨析:对三角公式不熟,不理解逻辑连结词“或”、“且”的意义,导致结论错误。
正解:在△ABC中,∵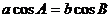 ,由正弦定理,
,由正弦定理,
得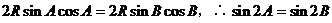 。
。
∴2A=2B或2A+2B=180°,
∴A=B或A+B=90°。
故△ABC为等腰三角形或直角三角形。
例5. 在△ABC中,已知a=2,b=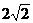 ,C=15°,求A。
,C=15°,求A。
错解:由余弦定理,得
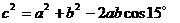
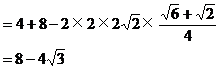
∴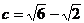 。
。
又由正弦定理,得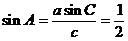
而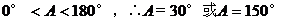 。
。
辨析:由题意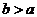 ,∴
,∴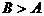 。因此A=150°是不可能的。错因是没有认真审题,未利用隐含条件。在解题时,要善于应用题中的条件,特别是隐含条件,全面细致地分析问题,避免错误发生。
。因此A=150°是不可能的。错因是没有认真审题,未利用隐含条件。在解题时,要善于应用题中的条件,特别是隐含条件,全面细致地分析问题,避免错误发生。
正解:同上 ,
,
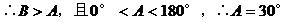 。
。
例4. 在△ABC中,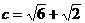 ,C=30°,求a+b的最大值。
,C=30°,求a+b的最大值。
错解:∵C=30°,∴A+B=150°,B=150°-A。
由正弦定理,得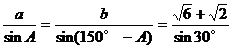
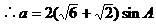 ,
,
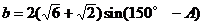
又∵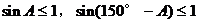
∴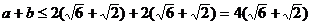 。
。
故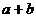 的最大值为
的最大值为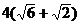 。
。
辨析:错因是未弄清A与150°-A之间的关系。这里A与150°-A是相互制约的,不是相互独立的两个量,sinA与sin(150°-A)不能同时取最大值1,因此所得的结果也是错误的。
正解:∵C=30°,∴A+B=150°,B=150°-A。
由正弦定理,得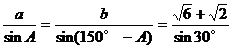
因此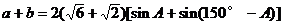
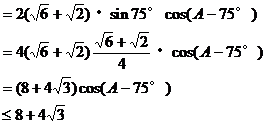
∴a+b的最大值为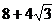 。
。
例3. 在△ABC中,A=60°,b=1,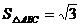 ,求
,求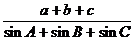 的值。
的值。
错解:∵A=60°,b=1,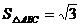 ,又
,又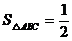
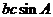 ,
,
∴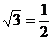
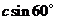 ,解得c=4。
,解得c=4。
由余弦定理,得
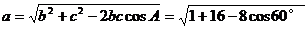
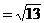
又由正弦定理,得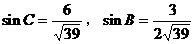 。
。
∴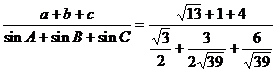 。
。
辨析:如此复杂的算式,计算困难。其原因是公式不熟、方法不当造成的。
正解:由已知可得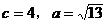 。由正弦定理,得
。由正弦定理,得
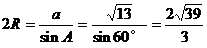 。
。
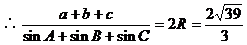 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com