
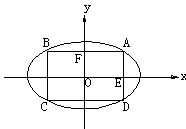
例1 求椭圆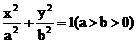 的内接矩形的面积及周长的最大值。
的内接矩形的面积及周长的最大值。
解:如图,设椭圆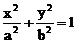 的内接矩形在第一象限的顶点是A(
的内接矩形在第一象限的顶点是A(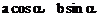 )(
)(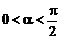 ),矩形的面积和周长分别是S、L。
),矩形的面积和周长分别是S、L。
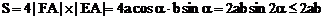 ,
,
当且仅当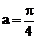 时,
时,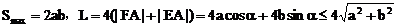 ,
,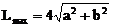 ,此时α存在。
,此时α存在。
2. 求和椭圆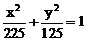 有相同离心率且通径(过焦点且垂直于长轴的直线与椭圆所交的线段)长等于5的椭圆方程。
有相同离心率且通径(过焦点且垂直于长轴的直线与椭圆所交的线段)长等于5的椭圆方程。
例. 求和椭圆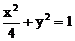 有相同离心率,且与直线
有相同离心率,且与直线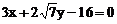 相切的椭圆方程。(2003年全国重点名校高考模拟题)
相切的椭圆方程。(2003年全国重点名校高考模拟题)
解法1:由以上性质,可设所求椭圆方程为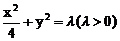 。因其与直线
。因其与直线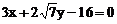 相切,故由方程组
相切,故由方程组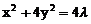 ,
,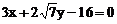 联立消去x,整理得
联立消去x,整理得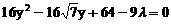 。其判别式
。其判别式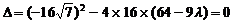 ,解得
,解得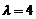 ,故所求椭圆方程为
,故所求椭圆方程为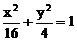
解法2:设所求椭圆方程为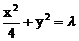 ,即
,即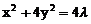 。因它与直线
。因它与直线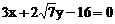 相切,则设切点为(x1,y1),故切线方程为
相切,则设切点为(x1,y1),故切线方程为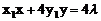 。两直线表示为同一直线,所以
。两直线表示为同一直线,所以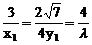 ,
,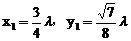 。将x1和y1同时代入椭圆方程,得
。将x1和y1同时代入椭圆方程,得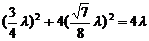 ,化简整理得
,化简整理得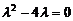 ,解得
,解得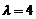 或
或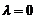 (舍去)。故所求椭圆方程为
(舍去)。故所求椭圆方程为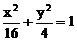
解法3:设所求椭圆方程为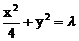 ,即
,即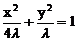 。则
。则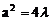 ,
,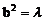 ,
,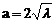 ,
,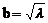 。设切点为(
。设切点为(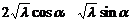 ),则椭圆的切线方程为
),则椭圆的切线方程为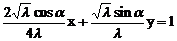 ,因为它和直线
,因为它和直线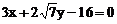 重合,得
重合,得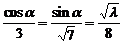 ,
,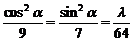 。由等比性质得
。由等比性质得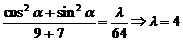 。故所求椭圆方程是
。故所求椭圆方程是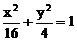
练一练
1. 求和椭圆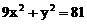 有相同离心率且过点(3,9)的椭圆方程。
有相同离心率且过点(3,9)的椭圆方程。
求证:和椭圆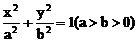 有相同离心率的椭圆方程都具有
有相同离心率的椭圆方程都具有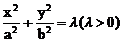 的特征。
的特征。
证明:设椭圆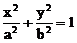 和椭圆
和椭圆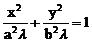 的离心率分别为e和e',则
的离心率分别为e和e',则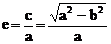 ,
,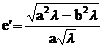
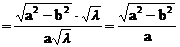
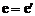 ,故椭圆
,故椭圆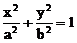 和椭圆
和椭圆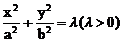 有相同的离心率。
有相同的离心率。
也就是说,和椭圆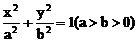 有相同的离心率的椭圆方程都具有
有相同的离心率的椭圆方程都具有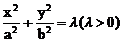 的特征。
的特征。
例9 设x,y为正数,不等式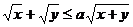 恒成立,求a的取值范围。
恒成立,求a的取值范围。
解:设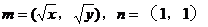 ,则
,则
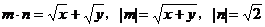
由性质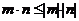 ,得
,得
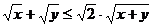
又不等式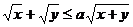 恒成立
恒成立
故有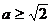
黑龙江省大庆市66中学(163000)
|
年级 |
高中 |
学科 |
数学 |
版本 |
|
期数 |
|
||||||
|
内容标题 |
构造向量巧解有关不等式问题 |
||||||||||||
|
分类索引号 |
G.622.46 |
分类索引描述 |
辅导与自学 |
||||||||||
|
主题词 |
构造向量巧解有关不等式问题 |
栏目名称 |
专题辅导 |
||||||||||
|
供稿老师 |
|
审稿老师 |
|
||||||||||
|
录入 |
侯海静 |
一校 |
胡丹 |
二校 |
|
审核 |
|
||||||
例7 已知m,n,x,y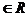 ,且
,且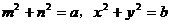 ,那么mx+ny的最大值为( )
,那么mx+ny的最大值为( )
A.
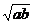 B.
B.
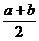
C.
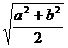 D.
D.
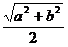
解:设p=(m,n),q=(x,y),则
由数量积的坐标运算,得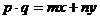
而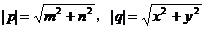
从而有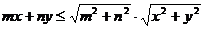
当p与q同向时,mx+ny取最大值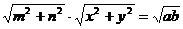 ,故选(A)。
,故选(A)。
例8 求函数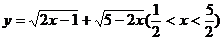 的最大值。
的最大值。
解:设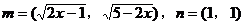 ,则
,则
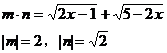
由性质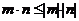 ,得
,得
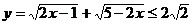
当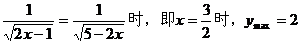
例6 已知m,n,a,b,c,d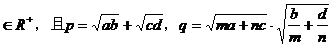 ,那么p,q的大小关系为( )
,那么p,q的大小关系为( )
A.
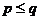 B.
B.
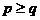 C.
p<q D.
p,q大小不能确定
C.
p<q D.
p,q大小不能确定
解:设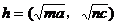 ,
,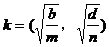 ,则
,则
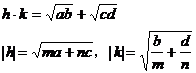
由性质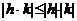 得
得
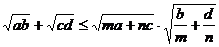
即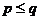 ,故选(A)
,故选(A)
例1 已知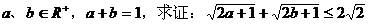 。
。
证明:设m=(1,1),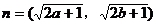 ,则
,则
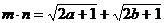
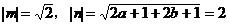
由性质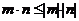 ,得
,得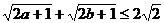
例2 已知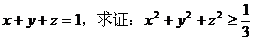 。
。
证明:设m=(1,1,1),n=(x,y,z),则
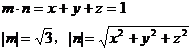
由性质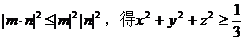
例3 已知a,b,c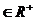 ,求证:
,求证: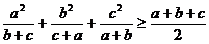 。
。
证明:设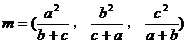 ,
,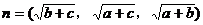 ,
,
则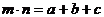
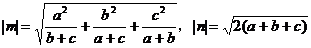
由性质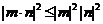 ,得
,得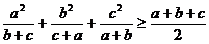
例4 已知a,b为正数,求证: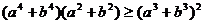 。
。
证明:设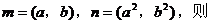
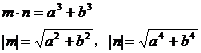
由性质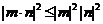 ,得
,得
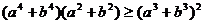
例5 设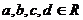 ,求证:
,求证: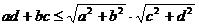 。
。
证明:设m=(a,b),n=(c,d),则
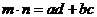
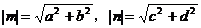
由性质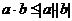 ,得
,得
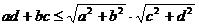
例5. 将6个同学平均分成3组有多少种分法?
错解:分法有: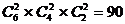 (种)
(种)
分析:若将6个同学编号,假如分组情况如下:1、2;3、4;5、6。先挑出1、2与后挑出1、2是同一情况,没有先后顺序差别,上面的解法产生了重复。
正解:分法有: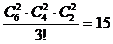 (种)
(种)
一般地,把不同的元素平均分成几组,就除以几的阶乘。
相关练习:
将5个不同礼品分成3组,则有几种分法?
|
年级 |
高中 |
学科 |
数学 |
版本 |
|
期数 |
|
||||||
|
内容标题 |
有关重复的排列组合问题 |
||||||||||||
|
分类索引号 |
G.622.475 |
分类索引描述 |
统考试题与题解 |
||||||||||
|
主题词 |
有关重复的排列组合问题 |
栏目名称 |
专题辅导 |
||||||||||
|
供稿老师 |
|
审稿老师 |
|
||||||||||
|
录入 |
韩秋荣 |
一校 |
胡丹 |
二校 |
|
审核 |
|
||||||
2. 某校准备参加2006年全国数学联赛,把10个名额分给高三8个班,不同的分配方案有几种?(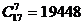 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com